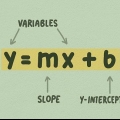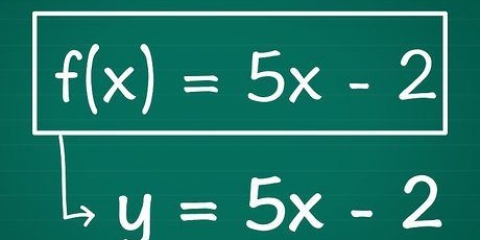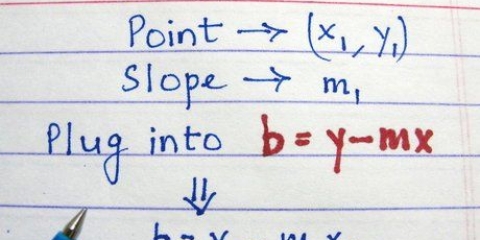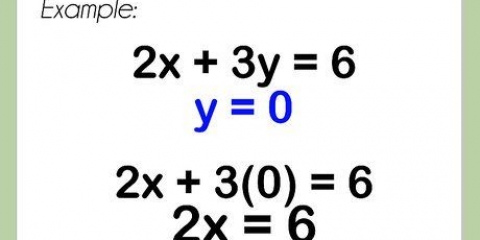Den Schnittpunkt einer Gleichung mit der Y-Achse finden

Schritte
Tipps

Der y-Achsenabschnitt einer Gleichung ist der Punkt, an dem sich der Graph einer Gleichung mit der y-Achse schneidet. Es gibt mehrere Möglichkeiten, diese Kreuzung zu finden, abhängig von den Informationen zu Beginn Ihres Befehls.

Schritte

Methode 1 von 3: Ermitteln des Schnittpunkts mit der y-Achse unter Verwendung der Steigung

1. Beachten Sie die Steigung. Die Steigung von `y über x` ist eine einzelne Zahl, die die Steigung einer Geraden angibt. Diese Art von Problem gibt Ihnen auch die (x,y)-Koordinate eines Punktes auf dem Graphen. Wenn Sie diese beiden Details nicht haben, fahren Sie mit den anderen Methoden unten fort.

Beispiel 1: Eine Gerade mit Steigung 2 geht durch den punkt (-3.4). Bestimmen Sie den Schnittpunkt mit der y-Achse dieser Linie mit den folgenden Schritten.

2. Lerne die übliche Form einer linearen Gleichung. Jede gerade Linie kann geschrieben werden als y = mx + b. Wenn die Gleichung in dieser Form vorliegt, ist m die Steigung und die Konstante B der Schnittpunkt mit der y-Achse.

3. Ersetzen Sie die Steigung in dieser Gleichung. Schreiben Sie die lineare Gleichung auf, aber statt m nutzt du die Steigung deiner Linie.

Beispiel 1 (Fortsetzung):y = mx + b
m = Steigung = 2
y = 2x + b

4. Ersetze x und y durch die Koordinaten des Punktes. Wenn Sie die Koordinaten eines Punktes auf der Linie haben, können Sie x und ja-Ersatzkoordinaten für die x und ja in deiner linearen Gleichung. Tun Sie dies für den Vergleich Ihrer Aufgabe.

Beispiel 1 (Fortsetzung): Der Punkt (3,4) liegt auf dieser Linie. An diesem Punkt, x = 3 und y = 4.
Ersetzen Sie diese Werte in ja = 2x +B:
4 = 2(3) + b

5. Lösen für B. Vergessen Sie nicht, B ist der Schnittpunkt mit der y-Achse der Geraden. Jetzt B die einzige Variable in der Gleichung ist, ordnen Sie die Gleichung um, um sie nach dieser Variablen aufzulösen, und finden Sie die Antwort.

Beispiel 1 (Fortsetzung):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
Der Schnittpunkt dieser Linie mit der y-Achse ist -2.

6. Schreiben Sie dies als Koordinate auf. Der Schnittpunkt mit der y-Achse ist der Schnittpunkt der Geraden mit der y-Achse. Da die y-Achse durch den Punkt x = 0 geht, ist die x-Koordinate des Schnittpunkts mit der y-Achse immer 0.

Beispiel 1 (Fortsetzung): Der Schnittpunkt mit der y-Achse liegt bei y = -2, also ist der Koordinatenpunkt (0, -2).

Methode 2 von 3: Verwenden von zwei Punkten

1. Notieren Sie sich die Koordinaten beider Punkte. Diese Methode behandelt Probleme, bei denen nur zwei Punkte auf einer Geraden gegeben sind. Schreiben Sie jede Koordinate in der Form (x,y).

2. Beispiel 2: Eine gerade Linie geht durch die Punkte (1, 2) und (3, -4). Bestimmen Sie den Schnittpunkt mit der y-Achse dieser Linie mit den folgenden Schritten.

3. Berechnen Sie die x- und y-Werte. Die Steigung oder Steigung ist ein Maß dafür, wie stark sich die Linie in vertikaler Richtung für jeden Schritt in horizontaler Richtung bewegt. Sie kennen dies vielleicht als `y über x` (

\frac{ja}{x}

${frac{y}{x}}$ ). So ermitteln Sie diese Werte anhand von zwei Punkten:

Die Änderung von `y` ist die Änderung in vertikaler Richtung oder die Differenz zwischen den ja-Werte der beiden Punkte.

Die Änderung von `x` ist die Änderung in horizontaler Richtung oder die Differenz zwischen den x-Werte der beiden Punkte.

Beispiel 2 (Fortsetzung): Die y-Werte der beiden Punkte sind 2 und -4, also steigt die Linie in vertikaler Richtung mit (-4) - (2) = -6.
Die x-Werte der beiden Punkte (in der gleichen Reihenfolge) sind 1 und 3, also erhöht sich die Linie horizontal um 3 - 1 = 2.

4. Dividiere y durch x, um die Steigung zu bestimmen. Da Sie diese beiden Werte nun kennen, können Sie sie in `

\frac{ja}{x}

${frac{y}{x}}$ ` zur Bestimmung der Steigung der Geraden.

Beispiel 2 (Fortsetzung):

S l Ö P e = \frac{ja}{x} = - 6 2 =

$Steigung={frac{y}{x}}={frac{-6}{2}}=$ -3.

5. Schauen Sie sich noch einmal die Standardform einer linearen Gleichung an. Sie können eine Gerade mit der Formel beschreiben y = mx + b, wodurch m die Steigung ist und B der Schnittpunkt mit der y-Achse. Jetzt haben wir die Steigung m und einem Punkt (x,y) können wir diese Gleichung verwenden, um zu finden B lösen (der Schnittpunkt mit der y-Achse).

6. Tragen Sie die Steigung und den Punkt in die Gleichung ein. Nimm die Gleichung in Standardform und ersetze m nach der berechneten Steigung. Ersetzen Sie die Variablen x und ja durch die Koordinaten eines einzelnen Punktes auf der Linie. Es spielt keine Rolle, welchen Punkt Sie verwenden.

Beispiel 2 (Fortsetzung): y = mx + b
Steigung = m = -3, also y = -3x + b
Die Gerade geht durch einen Punkt mit (x,y)-Koordinaten (1,2), also 2 = -3(1) + b.

7. Auflösen nach b. Jetzt ist die einzige verbleibende Variable in der Gleichung B, der Schnittpunkt mit der y-Achse. Ordne die Gleichung so um, dass B auf einer Seite der Gleichung, und du hast deine Antwort. Denken Sie daran, dass der Schnittpunkt mit der y-Achse immer eine x-Koordinate von 0 . hat.

Beispiel 2 (Fortsetzung): 2 = -3(1) + b
2 = -3 + b
5 = b
Der Schnittpunkt mit der y-Achse ist (0.5).

Methode 3 von 3: Verwenden einer Gleichung

1. Schreibe die Geradengleichung auf. Wenn Sie die Geradengleichung haben, können Sie mit ein wenig Algebra den Schnittpunkt mit der y-Achse bestimmen.

Beispiel 3: Was ist der Schnittpunkt mit der y-Achse der Geraden x + 4y = 16?
Hinweis: Beispiel 3 ist eine gerade Linie. Am Ende dieses Abschnitts finden Sie ein Beispiel für eine quadratische Gleichung (mit einer mit 2 potenzierten Variablen).

2. Ersetze 0 für x. Die y-Achse ist eine vertikale Linie durch x = 0. Dies bedeutet, dass jeder Punkt auf der y-Achse eine x-Koordinate von 0 hat, einschließlich des Schnittpunkts der Linie mit der y-Achse. Geben Sie 0 für x in die Gleichung ein.

Beispiel 3 (Fortsetzung): x + 4y = 16
x = 0
0 + 4y = 16
4y = 16

3. Für dich auflösen. Die Antwort ist der Schnittpunkt der Geraden mit der y-Achse.

Beispiel 3 (Fortsetzung): 4y = 16

4 ja 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
Der Schnittpunkt der Linie mit der y-Achse beträgt 4.

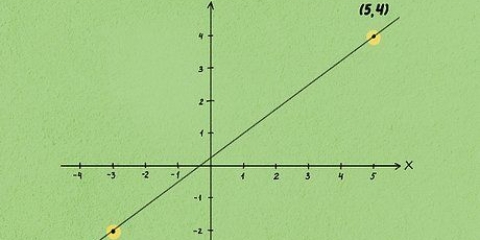
4. Bestätigen Sie dies, indem Sie eine Grafik zeichnen (optional). Überprüfen Sie Ihre Antwort, indem Sie die Gleichung so genau wie möglich grafisch darstellen. Der Punkt, an dem die Linie durch die y-Achse verläuft, ist der Schnittpunkt mit der y-Achse.

5. Finden Sie den Schnittpunkt mit der y-Achse einer quadratischen Gleichung. Eine quadratische Gleichung hat eine Variable (x oder y), die in die zweite Potenz erhoben wird. Mit der gleichen Substitution können Sie nach y auflösen, aber da die quadratische Gleichung eine Kurve ist, kann sie die y-Achse an 0, 1 oder 2 Punkten schneiden. Das bedeutet, dass Sie am Ende 0, 1 oder 2 Antworten erhalten.

Beispiel 4: Um den Schnittpunkt von zu finden

ja 2 = x + 1

$y^{2}=x+1$ mit der y-Achse ersetzt man x = 0 und löse die quadratische Gleichung.
In diesem Fall können wir

ja 2 = 0 + 1

$j^{2}=0+1$ löse durch Ziehen der Quadratwurzel beider Seiten. Denken Sie daran, dass Sie beim Ziehen einer Quadratwurzel zwei Antworten erhalten: eine negative und eine positive Antwort.

\sqrt{ja} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 oder y = -1. Diese sind beide Schnittpunkte mit der y-Achse dieser Kurve.

Tipps

Einige Länder verwenden a C oder eine andere Variable für B in der Gleichung y = mx + b. Seine Bedeutung bleibt jedoch dieselbe; es ist nur eine andere Schreibweise.
Für kompliziertere Gleichungen können Sie die Terme mit ja auf einer Seite der Gleichung isolieren.
Bei der Berechnung der Steigung zwischen zwei Punkten können Sie x und ja-Subtrahieren Sie die Koordinaten in beliebiger Reihenfolge, solange Sie den Punkt sowohl für y als auch für x in die gleiche Reihenfolge bringen. Beispielsweise kann die Steigung zwischen (1, 12) und (3, 7) auf zwei verschiedene Arten berechnet werden:

Zweiter Punkt – erster Punkt: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2,5$
Erster Punkt – zweiter Punkt: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2,5$