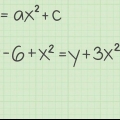Die Gleichung einer Tangente finden: 4 Schritte (mit Bildern)

Eine Tangente an eine Parabel oder Kurve ist eine Linie, die die Kurve nur an einem bestimmten Punkt berührt. Um die Gleichung dieser Tangente zu finden, müssen Sie die Steigung der Kurve an diesem Punkt berechnen, was einige mathematische Berechnungen erfordert. Sie können dann die Gleichung der Tangente in einer Punkt-Neigungs-Form schreiben. In diesem Artikel werden die erforderlichen Schritte erklärt.

Schritte

Finden Sie die Gleichung einer Tangentenlinie Schritt 1

1. Die Kurvengleichung kann als Funktion ausgedrückt werden. Berechnen Sie die Ableitung dieser Funktion, um die Steigungsgleichung dieser Kurve zu finden.

Der einfachste Weg, die meisten Polynome zu differenzieren, ist die Kettenregel. Multiplizieren Sie jede Gleichung der Funktion mit ihrer Potenz, um den Koeffizienten dieses Termes in der Ableitung zu finden, und subtrahieren Sie dann die Potenz von 1.
Beispiel: Für die Funktion f(x) = x^3 + 2x^2 + 5x + 1 ist die Ableitung f`(x) = 3x^2 + 4x + 5.
Für f(x) = (2x+5)^10 + 2*(4x+3)^5 ist die Ableitung f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Finden Sie die Gleichung einer Tangentenlinie Schritt 2

2. Wenn alles in Ordnung ist, werden die Koordinaten angegeben, an denen die Tangente auf die Kurve trifft. Setze den x-Wert dieses Punktes in die Ableitungsfunktion ein, um die Steigung der Kurve an diesem Punkt zu finden.

Für x = 2 ist der Punkt auf der Kurve (2.27) weil f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

Für f`(x) = 3x^2 + 4x + 5 ist die Steigung in (2.27) ist f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Finden Sie die Gleichung einer Tangentenlinie Schritt 3

3. Diese Steigung ist auch die Steigung der Tangente. Jetzt haben Sie die Steigung und den Punkt dieser Geraden, also können Sie die Gleichung der Geraden in Punkt-Neigungs-Form schreiben, oder y - y1 = m(x - x1).

In der Punkt-Steigungs-Form ist m die Piste und (x1,y1) sind die Koordinaten des Punktes. In diesem Beispiel wird die Gleichung also y - 27 = 25(x - 2).

Finden Sie die Gleichung einer Tangentenlinie Schritt 4

4. Es kann auch erforderlich sein, diese Gleichung in eine andere Form umzuwandeln, um die endgültige Antwort zu erhalten, falls die Anweisungen zu dem Problem dies erfordern.