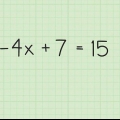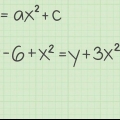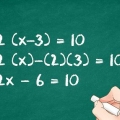4(x+3) + 9 - 5 = 32 
4x + 12 + 9 - 5 = 32 
4x+21-5 = 32 4x+16 = 32 4x + 16 - 16 = 32 - 16 4x = 16 
4x/4 = 16/4 x = 4 
2(x+3)+ 9 - 5 = 32 2(4+3)+ 9 - 5 = 32 2(7) + 9 - 5 = 32 4(7) + 9 - 5 = 32 28 + 9 - 5 = 32 37 - 5 = 32 32 = 32 

2x+12-12 = 44-12 2x = 32 
(2x)/2 = 32/2 x = 16 

2x + 12 = 44 2 x (4) + 12 = 44 2 x 16 + 12 = 44 32 + 12 = 44 44 = 44 

(x + 3)/6 = 2/3 6 x 2 = 12 (x + 3) x 3 = 3x + 9 3x + 9 = 12 
3x + 9 - 9 = 12 - 9 3x = 3 

(x + 3)/6 = 2/3 (1 + 3)/6 = 2/3 4/6 = 2/3 2/3 = 2/3 

√(2x+9) - 5 + 5 = 0 + 5 (2x+9) = 5 
(√(2x+9)) = 5 2x + 9 = 25 
2x + 9 - 9 = 25 - 9 2x = 16 

(2x+9) - 5 = 0 (2(8)+9) - 5 = 0 √(16+9) - 5 = 0 (25) - 5 = 0 5 - 5 = 0 

|4x +2| - 6 = 8 |4x +2| - 6 + 6 = 8 + 6 |4x +2| = 14 
4x + 2 = 14 4x + 2 - 2 = 14 -2 4x = 12 x = 3 
4x + 2 = -14 4x + 2 - 2 = -14 - 2 4x = -16 4x/4 = -16/4 x = -4 
(Für x = 3): |4x +2| - 6 = 8 |4(3) +2| - 6 = 8 |12 +2| - 6 = 8 |14| - 6 = 8 14 - 6 = 8 8 = 8 (für x = -4): |4x +2| - 6 = 8 |4(-4) +2| - 6 = 8 |-16 +2| - 6 = 8 |-14| - 6 = 8 14 - 6 = 8 8 = 8
Löse x in einer gleichung
Es gibt mehrere Möglichkeiten, x in einer Gleichung zu lösen, egal ob Sie mit Exponenten und Nullstellen arbeiten oder einfach nur dividieren oder multiplizieren müssen. Welche Methode Sie auch verwenden, Sie sollten immer einen Weg finden, x von einer Seite der Gleichung zu isolieren, damit Sie den Wert berechnen können. So geht`s:
Schritte
Methode 1 von 5: Verwenden einer gewöhnlichen linearen Gleichung

1. Schreiben Sie das Problem auf. Hier ist die Aufgabe:
- 2(x+3) + 9 - 5 = 32

2. Berechnen Sie den Exponenten. Denken Sie an die Reihenfolge der Operationen: HMVDOA, was für Klammern, Exponentiation, Division/Multiplikation, Addition/Subtraktion steht. In diesem Fall können Sie nicht zuerst herausfinden, was in Klammern steht, weil das x dazu gehört, also beginnen Sie mit der Potenz 2. 2 = 4

3. Berechnen Sie die Multiplikation. 4 mit (x+3) multiplizieren. Hier ist wie:

4. Berechnen Sie nun die Addition und Subtraktion. Addiere oder subtrahiere einfach die restlichen Zahlen. Hier ist wie:

5. Isolieren Sie die Variable. Sie tun dies, indem Sie beide Seiten der Gleichung durch 4 teilen, um x . zu finden. 4x/4 = x und 16/4 = 4, also x = 4.

6. Überprüfen Sie Ihre Berechnung. Setze x = 4 wieder in die ursprüngliche Gleichung ein, um sicherzustellen, dass sie richtig ist. Hier ist wie:
Methode 2 von 5: Mit Potenzierung

1. Schreiben Sie das Problem auf. Nehmen wir an, Sie arbeiten an einem Problem, bei dem der x-Term auch einen Exponenten enthält:
- 2x + 12 = 44

2. Isoliere den Term mit dem Exponenten. Das erste, was Sie jetzt tun sollten, ist, ähnliche Terme so zu kombinieren, dass alle Konstanten auf der rechten Seite der Gleichung stehen, während der Term mit dem Exponenten auf der linken Seite steht. Subtrahiere einfach 12 von beiden Seiten. Hier ist wie:

3. Isolieren Sie die Variable mit dem Exponenten, indem Sie beide Seiten durch den Koeffizienten des x-Terms dividieren. In diesem Fall ist 2 der x-Koeffizient, was bedeutet, dass beide Seiten durch 2 geteilt werden müssen, um ihn zu eliminieren. Hier ist wie:

4. Ziehe die Quadratwurzel jeder Seite der Gleichung. Wenn Sie die Quadratwurzel von x berechnen, haben Sie links x und rechts die Quadratwurzel von 16,4. Also x = 4.

5. Überprüfen Sie Ihre Berechnung. Setze x = 4 wieder in die ursprüngliche Gleichung ein, um sicherzustellen, dass sie richtig ist. Hier ist wie:
Methode 3 von 5: Verwenden Sie Brüche

1. Schreiben Sie das Problem auf. Nehmen wir an, Sie haben mit folgendem Problem zu tun:
- (x + 3)/6 = 2/3

2. Kreuzmultiplizieren. Um kreuzweise zu multiplizieren, multiplizieren Sie den Nenner jedes Bruchs mit dem Zähler des anderen Bruchs. Multiplizieren Sie also 6 (den ersten Nenner) mit 2 (den zweiten Zähler), um 12 auf der rechten Seite der Gleichung zu erhalten.Dann multipliziere 3 (der zweite Nenner) mit x + 3 (der erste Zähler), um 3 x + 9 links von der Gleichung zu erhalten. So wird das aussehen:

3. Kombiniere ähnliche Begriffe. Kombinieren Sie die Konstanten in der Gleichung, indem Sie 9 von beiden Seiten der Gleichung subtrahieren. Hier ist, was zu tun ist:

4. Isoliere x, indem du jeden Term durch den x-Koeffizienten dividierst. Teilen Sie einfach 3x und 9 durch 3, den Koeffizienten von x, und lösen Sie nach x . auf. 3x/3 = x und 3/3 = 1, also bleibt x = 1.

5. Überprüfen Sie Ihre Berechnung. Um deine Arbeit zu überprüfen, setze x wieder in die ursprüngliche Gleichung ein, um sicherzustellen, dass sie richtig ist. Hier ist, was zu tun ist:
Methode 4 von 5: Verwenden von Root-Zeichen

1. Schreiben Sie das Problem auf. Nehmen wir an, Sie lösen x in der folgenden Aufgabe:
- (2x+9) - 5 = 0

2. Isolieren Sie die Quadratwurzel. Sie müssen den Quadratwurzelteil der Gleichung links von der Gleichung isolieren, bevor Sie fortfahren können. Also addierst du 5 zu beiden Seiten der Gleichung. Hier ist wie:

3. Ziehe die Quadratwurzel von beiden Seiten. So wie Sie beide Seiten einer Gleichung durch den mit x multiplizierten Koeffizienten dividieren, müssen Sie auch die Quadratwurzel beider Seiten einer Gleichung ziehen, wenn x unter dem Wurzelzeichen liegt. Dies entfernt das Radikal aus der Gleichung. So geht`s:

4. Kombiniere ähnliche Begriffe. Kombinieren Sie gleiche Terme, indem Sie 9 von beiden Seiten der Gleichung subtrahieren, sodass alle Konstanten rechts liegen, während x links bleibt. Hier ist, was zu tun ist:

5. Isolieren Sie die Variable. Das letzte, was Sie tun müssen, um nach x aufzulösen, besteht darin, die Variable zu isolieren, indem Sie beide Seiten der Gleichung durch 2 dividieren, den Koeffizienten des x-Terms. 2x/2 = x und 16/2 = 8, also bleibt x = 8.

6. Überprüfen Sie Ihre Berechnung. Geben Sie für x erneut 8 in die Gleichung ein, um zu überprüfen, ob Ihre Berechnung richtig ist:
Methode 5 von 5: Verwenden Sie den Absolutwert

1. Schreiben Sie das Problem auf. Nehmen wir an, Sie versuchen, x im folgenden Problem zu lösen:
- |4x +2| - 6 = 8

2. Isolieren Sie den absoluten Wert. Das erste, was Sie tun müssen, ist, gleiche Terme zu kombinieren und den Absolutwert zu isolieren. In diesem Fall können Sie dies tun, indem Sie auf beiden Seiten der Gleichung 6 hinzufügen. Hier ist wie:

3. Entferne den Absolutwert und löse die Gleichung. Dies ist der erste und einfachste Schritt. Sie müssen x jetzt zweimal lösen, jedes Mal, wenn Sie mit einem Absolutwert arbeiten. So machen Sie dies beim ersten Mal:

4. Entfernen Sie den Absolutwert und ändern Sie das Vorzeichen der Terme auf der anderen Seite des Gleichheitszeichens, bevor Sie mit der Lösung fortfahren. Tun Sie dies jetzt noch einmal, und machen Sie diesmal den linken Teil der Gleichung gleich -14 statt 14. Hier ist wie:

5. Überprüfen Sie Ihre Berechnung. Jetzt, da Sie wissen, dass x = (3, -4) ist, setzen Sie einfach beide Zahlen wieder in die Gleichung ein, um sicherzustellen, dass sie richtig ist. Hier ist wie:
Tipps
- Um Ihre Arbeit zu überprüfen, geben Sie den Wert von x wieder in die ursprüngliche Gleichung ein und lösen Sie danach auf.
- Wurzeln sind eine weitere Möglichkeit, Exponenten darzustellen.Die Quadratwurzel von x = x^1/2.
Оцените, пожалуйста статью