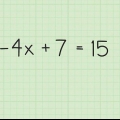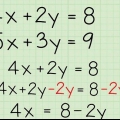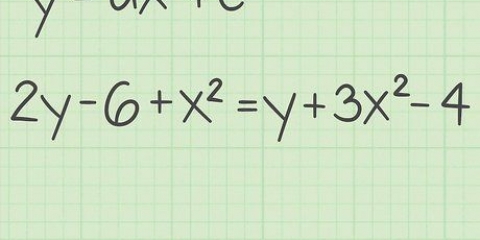Eine kubische Gleichung lösen

Schritte

Wenn Sie zum ersten Mal auf eine kubische Gleichung (der Form Axt + bx + cx + D=0) es mag fast unlösbar aussehen. Diese Methode zum Lösen kubischer Gleichungen gibt es jedoch schon seit Jahrhunderten! Es wurde im 16. Jahrhundert von den italienischen Mathematikern Niccolò Tartaglia und Gerolamo Cardano entdeckt. Es war eine der ersten Formeln, die den alten Griechen und Römern unbekannt war. Kubische Gleichungen zu lösen kann sehr schwierig sein, aber mit der richtigen Herangehensweise (und genügend Grundkenntnissen) können selbst die kniffligsten kubischen Gleichungen gezähmt werden.

Schritte

Methode 1 von 3: Mit der abc-Formel lösen

Bildtitel Löse eine kubische Gleichung Schritt 1

1. Überprüfe, ob die kubische Gleichung eine Konstante enthält. Wie oben angedeutet, haben kubische Gleichungen die Form Axt + bx + cx + D=0. b, c, und D kann 0 sein, ohne sich zu ändern, ob es sich um eine kubische Gleichung handelt oder nicht – im Wesentlichen bedeutet, dass eine Gleichung nicht aus allen Termen bestehen muss bx, cx oder D eine kubische Gleichung sein. Sie beginnen mit der Anwendung dieser relativ einfachen Methode zum Lösen kubischer Gleichungen, indem Sie zunächst prüfen, ob Ihre Gleichung eine Konstante (a D-bei dem die). Ist das nicht der Fall, dann kannst du de abc formel um die Antworten der Gleichung mit ein wenig Mathematik zu finden.

Wenn die Gleichung eine Konstante enthält, müssen Sie eine andere Methode verwenden. Siehe unten für alternative Ansätze.

Bildtitel Löse eine kubische Gleichung Schritt 2

2. auflösen x aus der Gleichung. Da Ihre Gleichung keine Konstante enthält, hat jeder Term in der Gleichung a x-Variable. Dies bedeutet, dass a x kann aus der Gleichung herausgerechnet werden, um sie zu vereinfachen. Tun Sie dies und schreiben Sie Ihre Gleichung in der Form um x(Axt + bx + C).

Angenommen, Sie haben die Gleichung 3x + -2x + 14x=0. Durch eine x außerhalb der Klammern erhalten wir x(3x + -2x + 14)=0.

Bildtitel Löse eine kubische Gleichung Schritt 3

3. Verwenden Sie die abc-Formel, um nach den Termen in Klammern aufzulösen. Sie haben vielleicht bemerkt, dass die Terme Ihrer neuen Gleichung in Klammern die Form einer quadratischen Gleichung haben (Axt + bx + C). Dies bedeutet, dass wir die Werte finden können, für die die quadratische Gleichung gleich Null ist um a, b und C in der abc-Formel ({-B +/-√ (B- 4ac)}/2ein). Dadurch finden Sie zwei der Antworten Ihrer kubischen Gleichung.

In unserer Beispielaussage tragen wir unsere Werte ein a, b und C (bzw. 3, -2 und 14) in der quadratischen Gleichung in:

{-B +/-√ (B- 4ac)}/2ein

{-(-2) +/-√ ((-2)-4(3)(14))}/2(3)

{2 +/-√ (4 - (12)(14))}/6

{2 +/-√ (4 - (168)}/6

{2 +/-√ (-164)}/6

Antwort 1:

{2 + √(-164)}/6

{2 + 12.8ich}/6

Antwort 2:

{2 - 12.8ich}/6

Bildtitel Löse eine kubische Gleichung Schritt 4

4. Verwenden Sie null und die quadratischen Antworten als Antworten auf Ihre kubische Gleichung. Vierseitige Gleichungen haben zwei Lösungen, aber kubische Gleichungen haben drei. Sie haben bereits zwei – das sind die Antworten, die Sie durch die Berechnung der "quadratischen Gleichung" in den Klammern gefunden haben. In den Fällen, in denen eine Gleichung für dieses `aus Klammern` geeignet ist, lautet die dritte Antwort immer 0 sind. Herzlichen Glückwunsch – Sie haben gerade eine kubische Gleichung gelöst.

Der Grund, warum dies funktioniert, hat mit der grundlegenden Tatsache zu tun, dass jede Zahl multipliziert mit Null ist gleich Null. Wenn Sie die Gleichung in die Form umwandeln x(Axt + bx + C)=0, man teilt die beiden im Wesentlichen in Teile: ein Teil ist der x-variabel außerhalb der Klammern und das andere ist das Quadrat innerhalb der Klammern. Wenn einer dieser Teile gleich Null ist, dann ist es auch die ganze Gleichung. Wenn also die beiden Antworten auf das Quadrat innerhalb der Klammern diesen Teil zu Null machen, dann machen die Antworten auf die kubische Gleichung auch den Teil außerhalb der Klammern gleich Null.

Methode 2 von 3: Lösung mithilfe von Faktorenlisten

Bildtitel Löse eine kubische Gleichung Schritt 5

1. Stellen Sie sicher, dass Ihre kubische Gleichung eine Konstante hat. Obwohl die obige Methode nützlich ist, da Sie keine neuen mathematischen Fähigkeiten erlernen müssen, funktioniert sie nicht immer zum Lösen kubischer Gleichungen. Wenn Ihre Gleichung in der Form ist Axt + bx + cx + D=0 Zustand, und D ungleich Null ist, funktionieren die Klammern nicht und Sie benötigen entweder diese Methode oder die im nächsten Teil.

Angenommen, Sie haben die gegebene Gleichung 2x + 9x + 13x=-6. In diesem Fall erfordert eine 0 rechts vom Gleichheitszeichen das Addieren von 6 auf beiden Seiten. Unsere neue Gleichung ist 2x + 9x + 13x + 6=0, D=6, also können wir die Klammern aus dem vorherigen Teil nicht verwenden.

Bildtitel Löse eine kubische Gleichung Schritt 6

2. Bestimmen Sie die Faktoren von ein und D. Um die kubische Gleichung zu lösen, bestimmen Sie zunächst die Faktoren von ein (der Koeffizient der x Bedingungen D (die Konstante am Ende der Gleichung). Zur Erinnerung: Faktoren sind die Zahlen, die miteinander multipliziert eine andere Zahl ergeben. Zum Beispiel, weil Ihre 6 aus der Multiplikation 6 entsteht &Zeit; 1 und 2 × 3, sind 1, 2, 3 und 6 Faktoren von 6.

In unserer Beispielaussage ein=2 und d=6. Die Faktoren von 2 sind 1 und 2. Die Faktoren von 6 sind 1, 2, 3 und 6.

Bildtitel Löse eine kubische Gleichung Schritt 7

3. Teilen Sie die Faktoren von ein durch die Faktoren von D. Jetzt listen Sie alle Werte auf, die Sie erhalten, indem Sie jeden Faktor teilen ein um irgendeinen Faktor D. Dies führt normalerweise zu vielen Brüchen und einigen ganzen Zahlen. Die ganzzahligen Lösungen Ihrer kubischen Gleichung sind entweder eine der ganzen Zahlen aus der Liste oder die negative Zahl einer dieser Zahlen.

In unserer Gleichung berechnen Sie die Faktoren von ein (1, 2) auf den Faktoren von D (1, 2, 3, 6) und Sie erhalten die folgende Liste: 1, 1/2, 1/3, 1/6, 2 und 2/3. Jetzt fügen wir die negativen Zahlen zur Liste hinzu, um sie zu vervollständigen: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 und -2/3. Die ganzzahlige Lösung unserer kubischen Gleichung finden Sie irgendwo in dieser Liste.

Bildtitel Löse eine kubische Gleichung Schritt 8

4. Verwenden Sie die synthetische Freigabe, um Ihre Antworten manuell zu überprüfen. Sobald Sie die Werteliste zusammengestellt haben, können Sie die ganzzahligen Lösungen Ihrer kubischen Gleichung finden, indem Sie schnell jede ganze Zahl manuell eingeben und prüfen, welche gleich Null sind. Wenn Sie keine Zeit damit verbringen möchten, gibt es eine etwas schnellere Methode gemäß eine Technik namens synthetisches Teilen. Das Wesentliche ist, dass Sie ganze Zahlen durch das Original dividieren a, b, c und D Koeffizienten deiner kubischen Gleichung. Bleibt ein Rest von 0 übrig, ist Ihr Wert eine der Lösungen der kubischen Gleichung.

Synthetic Sharing ist ein komplexes Thema – folgen Sie dem obigen Link für weitere Informationen. Hier ist ein Beispiel für das Finden einer der Lösungen unserer kubischen Gleichung durch synthetische Division:

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Da wir am Ende eine 0 als Rest haben, wissen wir, dass eine der Lösungen unserer kubischen Gleichung die ganze Zahl . ist -1 ist.

Methode 3 von 3: Verwendung der `Diskriminante`

Bildtitel Löse eine kubische Gleichung Schritt 9

1. Schreiben Sie die Werte von . aus a, b, c und D. Bei dieser Methode zum Auffinden der Lösungen einer kubischen Gleichung verlassen wir uns stark auf die Koeffizienten der Terme in unserer Gleichung. Aus diesem Grund ist es ratsam, die Begriffe zu verwenden a, b, c und D schreibe es auf, bevor du anfängst, damit du nicht vergisst, was jedes einzelne ist.

Zum Beispiel für den Vergleich x - 3x + 3x - 1, wir schreiben ein=1, B=-3, C=3 und D=-1. Vergiss das nicht von a x-Variable ohne Koeffizienten wird angenommen, dass der Koeffizient gleich 1 . ist.

Bildtitel Löse eine kubische Gleichung Schritt 10

2. Berechnen Sie Δ0=B - 3ac. Wenn Sie die Diskriminante zum Lösen kubischer Gleichungen verwenden, benötigen Sie etwas fortgeschrittenere Mathematik, aber wenn Sie das Verfahren sorgfältig befolgen, werden Sie feststellen, dass es ein wertvolles Werkzeug zum Lösen dieser bereits kniffligen kubischen Gleichungen ist. Beginnen Sie damit, Δ0 zu finden, den ersten von mehreren wichtigen Werten, die wir benötigen, indem Sie die entsprechenden Werte in der Formel einsetzen B - 3ac.

In unserem Beispielproblem lösen wir dies wie folgt:

B - 3ac

(-3) - 3(1)(3)

9 - 3(1)(3)

9 - 9=0=Δ0

Bildtitel Löse eine kubische Gleichung Schritt 11

3. Berechnen Sie Δ1=2B - 9ABC + 27einD. Die nächste wichtige Größe, die wir benötigen, Δ1, erfordert etwas mehr Arbeit, kann aber ähnlich wie Δ0 . gefunden werden. Ersetzen Sie die richtigen Werte in der Formel 2B - 9ABC + 27einD für den Wert von Δ1.

In unserem Beispielproblem lösen wir dies wie folgt:

2(-3) - 9(1)(-3)(3) + 27(1)(-1)

2(-27) - 9(-9) + 27(-1)

-54 + 81 - 27

81 - 81=0=Δ1

Bildtitel Löse eine kubische Gleichung Schritt 12

4. Berechne Δ=Δ1 - 4Δ0) ÷ -27ein. Dann berechnen wir die diskriminierend der kubischen Gleichung aus den Werten für Δ0 und Δ1. Eine Diskriminante ist einfach eine Zahl, die uns etwas über die Antworten eines Polynoms sagt (unbewusst kennen Sie vielleicht schon die quadratische Diskriminante: B - 4ac). Im Fall der kubischen Gleichung, wenn die Diskriminante positiv ist, hat die Gleichung drei reelle Lösungen. Wenn die Diskriminante null ist, hat die Gleichung eine oder zwei reelle Lösungen, und einige dieser Lösungen werden geteilt. Wenn sie negativ ist, hat die Gleichung nur eine Lösung. (Eine kubische Gleichung hat immer eine reelle Lösung, denn der Graph ist immer mindestens einmal mit x-Achsenschnitte.)

In unserem Beispielproblem ist die Bestimmung von Δ sehr einfach, da sowohl Δ0 als auch Δ1=0. Wir lösen das wie folgt:

1 - 4Δ0) ÷ -27ein

(0) - 4(0)) -27(1)

0 - 0 27

0=Δ, also hat unsere Gleichung 1 oder 2 Antworten.

Bildtitel Löse eine kubische Gleichung Schritt 13

5. Berechnung C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). Der letzte wichtige zu berechnende Wert ist C. Mit dieser wichtigen Größe können wir endlich die drei Lösungen finden. Lösen Sie dies wie gewohnt und ersetzen Sie 1 und Δ0, wo nötig.

In unserem Beispielproblem finden wir C folgendermaßen:

√(√((Δ1 - 4Δ0) + Δ1)/ 2)

√(√((0 - 4(0)) + (0))/ 2)

√(√((0 - 0) + (0))/ 2)

0=C

Bildtitel Löse eine kubische Gleichung Schritt 14

6. Berechnen Sie die drei Antworten mit Ihren Variablen. Die Antworten auf Ihre kubische Gleichung werden durch die Formel gegeben (B + uC + (Δ0/uC)) / 3ein, wodurch Sie=(-1 + √(-3))/2 und n ist 1, 2 oder 3. Geben Sie Ihre Werte ein, wo dies erforderlich ist, um dies zu lösen – dies erfordert viel Mathematik, sollte Ihnen jedoch drei mögliche Antworten geben!

In unserem Beispielproblem können wir dies lösen, indem wir die Antwort überprüfen, wenn n gleich 1, 2 oder 3 . ist. Die Antworten, die wir aus diesen Tests erhalten, sind die möglichen Antworten auf unsere kubische Gleichung – jede Lösung, die nach der Substitution in der Gleichung 0 ergibt, ist richtig. Angenommen, wir erhalten 1 als Antwort auf einen der Tests, da die Eingabe von 1 in x - 3x + 3x - 1 ergibt 0, wenn Antwort, dann 1 eine der Antworten auf unsere kubische Gleichung.