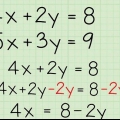2x - 2x = 0 4y - 2y = 2y 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2y = 6 Teile 2y und 6 durch 2 und erhalte y = 3 
Setze y = 3 in die Gleichung 2x + 2y = 2 ein und löse nach x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Du hast das Gleichungssystem durch Subtraktion gelöst. (x, y) = (-2, 3) 
Tragen Sie (-2, 3) für (x, y) in die Gleichung 2x + 4y = 8 . ein. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Tragen Sie (-2, 3) für (x, y) in die Gleichung 2x + 2y = 2 . ein. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6y + -6y = 0 8 + 4 = 12 Wenn Sie dies kombinieren, erhalten Sie ein neues Produkt: 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Teilen Sie 4x und 12 durch 3, um x = 3 . zu erhalten 
Setze x = 3 in die Gleichung x - 6y = 4 ein, um y . zu finden. 3 - 6y = 4 -6y = 1 Teile -6y und 1 durch -6, um y = -1/6 . zu erhalten. Du hast das Gleichungssystem mit Addition gelöst. (x, y) = (3, -1/6) 
Tragen Sie (3, -1/6) für (x, y) in die Gleichung ein 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Tragen Sie (3, -1/6) für (x, y) in die Gleichung ein x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Du hast das Gleichungssystem durch Multiplikation gelöst. (x, y) = (2, 2) 
Tragen Sie (2, 2) für (x, y) in die Gleichung ein 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Tragen Sie (2, 2) für (x, y) in die Gleichung ein 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3y = 9 2(2 - 4y) + 3y = 9 4 - 8 Jahre + 3 Jahre = 9 4 - 5 Jahre = 9 -5y = 9 - 4 -5y = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Du hast das Gleichungssystem durch Substitution gelöst. (x, y) = (6, -1) 
Tragen Sie (6, -1) für (x, y) in die Gleichung 2x + 3y = 9 . ein. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Setze (6, -1) für (x, y) in die Gleichung x + 4y = 2 . ein. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Lösen eines gleichungssystems
Um ein Gleichungssystem zu lösen, muss der Wert mehrerer Variablen in mehreren Gleichungen ermittelt werden. Sie können ein Gleichungssystem durch Addition, Subtraktion, Multiplikation oder Substitution lösen. Wenn Sie lernen möchten, wie man ein Gleichungssystem löst, müssen Sie nur diese Schritte ausführen.
Schritte
Methode 1 von 4: Durch Subtraktion lösen

1. Schreiben Sie eine Gleichung über die andere. Das Lösen dieser Gleichungen durch Subtraktion ist eine ideale Methode, wenn Sie sehen, dass beide Gleichungen dieselbe Variable mit demselben Koeffizienten und Vorzeichen haben. Wenn beispielsweise beide Gleichungen die Variable -2x haben, können Sie die Subtraktion verwenden, um den Wert beider Variablen zu ermitteln.
- Schreiben Sie eine Gleichung über die andere, sodass die x- und y-Variablen beider Gleichungen und die Zahlen untereinander liegen. Platziere das Minuszeichen neben der unteren Zahl.
- Beispiel: Wenn Sie die folgenden zwei Gleichungen haben: 2x + 4y = 8 und 2x + 2y = 2, würde das so aussehen:
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Subtrahiere ähnliche Begriffe. Nachdem die beiden Gleichungen nun ausgerichtet sind, müssen Sie nur noch die gleichen Terme subtrahieren. Tun Sie dies mit einem Begriff nach dem anderen:

3. Nach Restlaufzeit auflösen. Entfernen Sie alle Nullen aus der erstellten Gleichung, der Wert ändert sich nicht, und lösen Sie die verbleibende Gleichung.

4. Geben Sie den gefundenen Wert der Variablen in eine der Gleichungen ein. Da Sie nun wissen, dass y = 3 ist, können Sie diesen Wert in die ursprüngliche Gleichung einsetzen, um nach x . aufzulösen. Egal für welche Gleichung Sie sich entscheiden, die Antwort ist dieselbe. Verwenden Sie also die einfachste Gleichung!

5. Überprüfe deine Antwort. Um sicherzustellen, dass Ihre Antwort richtig ist, geben Sie beide Antworten in beide Gleichungen ein. So geht`s:
Methode 2 von 4: Durch Addition lösen

1. Schreiben Sie eine Gleichung über die andere. Das Lösen eines Gleichungssystems durch Addition ist die beste Methode, wenn Sie feststellen, dass beide Gleichungen eine Variable mit demselben Koeffizienten, aber mit unterschiedlichem Vorzeichen haben; wenn beispielsweise eine Gleichung die Variable 3x enthält und die andere die Variable -3x.
- Schreiben Sie eine Gleichung über die andere, sodass die x- und y-Variablen beider Gleichungen und die Zahlen untereinander liegen. Platziere das Pluszeichen neben der unteren Zahl.
- Beispiel: Sie haben die folgenden beiden Gleichungen 3x + 6y = 8 und x - 6y = 4, dann schreiben Sie die erste Gleichung über die zweite, wie unten gezeigt:
- 3x + 6y = 8
- +(x - 6y = 4)

2. Fügen Sie ähnliche Begriffe zusammen. Nachdem die beiden Gleichungen nun übereinander ausgerichtet sind, müssen Sie nur noch die Terme mit derselben Variablen addieren:

3. Nach Restlaufzeit auflösen. Entferne eine Null aus der entstandenen Gleichung, sie ändert den Wert nicht. Löse die verbleibende Gleichung.

4. Geben Sie den gefundenen Wert dieser Variablen in eine der Gleichungen ein. Da Sie nun wissen, dass x = 3 ist, können Sie diesen Wert in die ursprüngliche Gleichung einsetzen, um nach y . aufzulösen. Egal für welche Gleichung Sie sich entscheiden, die Antwort ist dieselbe. Verwenden Sie also die einfachste Gleichung!

5. Überprüfe deine Antwort. Um sicherzustellen, dass Ihre Antwort richtig ist, geben Sie beide Antworten in beide Gleichungen ein. So geht`s:
Methode 3 von 4: Durch Multiplikation lösen

1. Schreiben Sie eine Gleichung über die andere. Schreiben Sie eine Gleichung über die andere, sodass die x- und y-Variablen beider Gleichungen und die Zahlen untereinander liegen. Wenn Sie Multiplikation verwenden, tun Sie dies, weil keine der Variablen gleiche Koeffizienten hat - gerade jetzt.
- 3x + 2y = 10
- 2x - y = 2

2. Gleiche Koeffizienten sicherstellen. Multiplizieren Sie dann eine oder beide Gleichungen mit einer Zahl, sodass eine der Variablen denselben Koeffizienten hat. In diesem Fall können Sie die ganze zweite Gleichung mit 2 multiplizieren, so dass -y gleich -2y ist und somit der erste y-Koeffizient. So geht`s:

3. Addiere oder subtrahiere die Gleichungen. Jetzt müssen Sie nur noch gleiche Terme durch Addieren oder Subtrahieren eliminieren. Da es sich hier um 2y und -2y handelt, ist es sinnvoll, die Additionsmethode zu verwenden, da diese gleich 0 . ist. Wenn Sie es mit 2y + 2y zu tun haben, verwenden Sie die Subtraktionsmethode. Hier ist ein Beispiel für die Verwendung der Additionsmethode zum Eliminieren von Variablen:

4. Lösen Sie dies für die verbleibende Laufzeit auf. Dies lässt sich leicht lösen, indem Sie den Wert des Begriffs ermitteln, den Sie noch nicht eliminiert haben. Wenn 7x = 14, dann x = 2.

5. Geben Sie den gefundenen Wert in eine der Gleichungen ein. Geben Sie den Term in eine der ursprünglichen Gleichungen ein, um den anderen Term aufzulösen. Wähle dafür die einfachste Gleichung, das ist die schnellste.

6. Überprüfe deine Antwort. Um sicherzustellen, dass Ihre Antwort richtig ist, geben Sie beide Antworten in beide Gleichungen ein. So geht`s:
Methode 4 von 4: Durch Substitution lösen

1. Isolieren Sie eine Variable. Die Substitution ist ideal, wenn einer der Koeffizienten in einer der Gleichungen gleich 1 . ist. Dann musst du diese Variable nur noch auf eine Seite der Gleichung isolieren, um ihren Wert zu finden.
- Wenn Sie mit den Gleichungen 2x + 3y = 9 und x + 4y = 2 arbeiten, müssen Sie x in der zweiten Gleichung isolieren.
- x + 4y = 2
- x = 2 - 4y

2. Geben Sie den Wert der Variablen ein, die Sie in der anderen Gleichung isoliert haben. Nimm den Wert der isolierten Variablen und setze ihn in die andere Gleichung ein. Natürlich nicht in der gleichen Gleichung sonst löst du nichts. Hier ist ein Beispiel, wie das geht:

3. Nach der verbleibenden Variablen auflösen. Nun, da Sie wissen, dass y = - 1 ist, setzen Sie diesen Wert in die einfachere Gleichung ein, um den Wert von x . zu finden. Hier ist ein Beispiel dafür:

4. Überprüfe deine Antwort. Um sicherzustellen, dass Ihre Antwort richtig ist, geben Sie beide Antworten in beide Gleichungen ein. So geht`s:
Tipps
- Sie sollten nun in der Lage sein, jedes lineare Gleichungssystem durch Addition, Subtraktion, Multiplikation oder Substitution zu lösen, aber je nach Gleichung ist eine Methode in der Regel am besten geeignet.
"Lösen eines gleichungssystems"
Оцените, пожалуйста статью