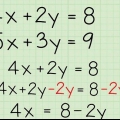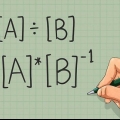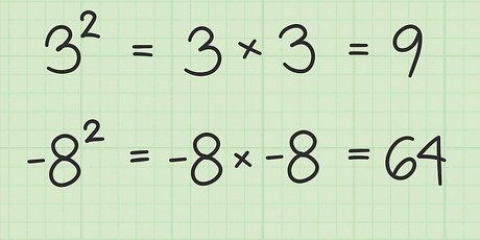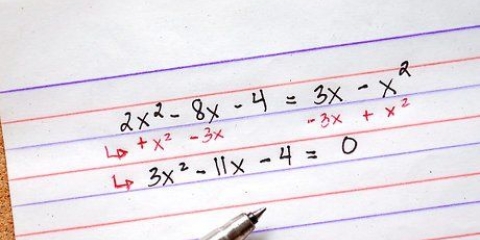Wenn Sie mehr Variablen haben, setzen Sie die Zeile einfach so lange fort, wie es dauert. Wenn Sie beispielsweise versuchen, ein System mit sechs Variablen zu lösen, sieht Ihre Standardform wie folgt aus: Au+Bv+Cw+Dx+Ey+Fz=G. In diesem Artikel konzentrieren wir uns auf Systeme mit nur drei Variablen. Das Lösen eines größeren Systems ist genau das gleiche, erfordert jedoch nur mehr Zeit und mehr Schritte. Beachten Sie, dass in der Standardform die Operationen zwischen den Termen immer eine Addition sind. Wenn Ihre Gleichung eine Subtraktion anstelle einer Addition enthält, müssen Sie später damit arbeiten, indem Sie Ihren Koeffizienten negativ machen. Um dies leichter zu merken, können Sie die Gleichung umschreiben und die Operation hinzufügen und den Koeffizienten negativ machen. Sie können beispielsweise die Gleichung 3x-2y+4z=1 umschreiben als 3x+(-2y)+4z=1. 
Angenommen, Sie haben ein System bestehend aus den drei Gleichungen 3x+y-z=9, 2x-2y+z=-3 und x+y+z=7. Die oberste Zeile Ihrer Matrix enthält die Zahlen 3, 1, -1, 9, da dies die Koeffizienten und die Lösung der ersten Gleichung sind. Beachten Sie, dass für jede Variable, die keinen Koeffizienten hat, ein Koeffizient von 1 . angenommen wird. Die zweite Zeile der Matrix wird 2, -2, 1, -3 und die dritte Zeile 1, 1, 1, 7. Stellen Sie sicher, dass die x-Koeffizienten in der ersten Spalte, die y-Koeffizienten in der zweiten, die z-Koeffizienten in der dritten und die Lösungsterme in der vierten Spalte ausgerichtet sind. Wenn Sie mit der Arbeit mit der Matrix fertig sind, werden diese Spalten beim Schreiben Ihrer Lösung wichtig sein. 

Sie können jede bestimmte Position in einer Matrix angeben, indem Sie eine Kombination von R und C . verwenden. Um beispielsweise einen Begriff in der zweiten Zeile, dritten Spalte zu bezeichnen, könnten Sie ihn R2C3 nennen. 

Es ist üblich, Brüche bei der Skalarmultiplikation zu verwenden, da Sie oft eine diagonale Reihe von Einsen erhalten möchten. Gewöhnen Sie sich an die Arbeit mit Brüchen. Es ist auch einfacher (für die meisten Schritte beim Lösen der Matrix), Ihre Brüche in unechter Form zu schreiben und sie dann für die endgültige Lösung wieder in gemischte Zahlen umzuwandeln. Deshalb ist es einfacher, mit der Zahl 1 2/3 zu arbeiten, wenn du sie als 5/3 schreibst. Zum Beispiel beginnt die erste Zeile (R1) unserer Beispielaufgabe mit den Termen [3.1,-1,9]. Die Lösungsmatrix muss an der ersten Stelle der ersten Zeile eine 1 enthalten. Um die 3 in eine 1 zu „verwandeln“, können wir die gesamte Reihe mit 1/3 multiplizieren. Dadurch entsteht das neue R1 von [1.1/3,-1/3.3]. Achte darauf, alle negativen Zeichen dort zu lassen, wo sie hingehören. 
Sie können die abgekürzte Notation verwenden und diese Operation als R2-R1=[0,-1,2,6] deklarieren. Denken Sie daran, dass Addition und Subtraktion genau entgegengesetzte Formen derselben Operation sind. Sie können sich das so vorstellen, als würden Sie zwei Zahlen addieren oder das Gegenteil subtrahieren. Wenn Sie beispielsweise mit der einfachen Gleichung 3-3=0 beginnen, können Sie sich dies als Additionsproblem von 3+(-3)=0 . vorstellen. Das Ergebnis ist das gleiche. Das scheint einfach, aber manchmal ist es einfacher, ein Problem in der einen oder anderen Form zu betrachten. Behalte einfach deine negativen Zeichen im Auge. 
Paar; dass es eine Reihe 1 von [1,1,2,6] und eine Reihe 2 von [2,3,1,1] gibt. Sie wollen einen 0-Term in der ersten Spalte von R2. Das heißt, Sie möchten die 2 in eine 0 ändern. Dazu müssen Sie 2 . subtrahieren. Sie können eine 2 erhalten, indem Sie zuerst Zeile 1 mit der Skalarmultiplikation 2 multiplizieren und dann die erste Zeile von der zweiten Zeile subtrahieren. In abgekürzter Form kann dies geschrieben werden als R2-2*R1. Multiplizieren Sie zuerst R1 mit 2, um [2,2,4,12] zu erhalten. Dann subtrahiere dies von R2, um [(2-2),(3-2),(1-4),(1-12)] zu erhalten. Vereinfachen Sie dies und Ihr neues R2 wird [0,1,-3,-11]. 
Ein häufiger Fehler tritt auf, wenn ein kombinierter Multiplikations- und Additionsschritt in einem Zug ausgeführt wird. Angenommen, Sie müssen R1 zweimal von R2 subtrahieren. Wenn Sie für diesen Schritt R1 mit 2 multiplizieren, denken Sie daran, dass sich R1 in der Matrix nicht ändert. Sie führen nur die Multiplikation durch, um R2 . zu ändern. Kopieren Sie zuerst R1 in seiner ursprünglichen Form, und ändern Sie dann in R2. 
1. Bilden Sie eine 1 in der ersten Zeile, erste Spalte (R1C1). 2. Machen Sie eine 0 in der zweiten Zeile, erste Spalte (R2C1). 3. Bilden Sie eine 1 in der zweiten Reihe, zweite Spalte (R2C2). 4. Machen Sie eine 0 in der dritten Zeile, erste Spalte (R3C1). 5. Machen Sie eine 0 in der dritten Zeile, zweite Spalte (R3C2). 6. Bilden Sie eine 1 in der dritten Reihe, dritte Spalte (R3C3). 
Erstellen Sie eine 0 in der zweiten Zeile, dritte Spalte (R2C3). Erstellen Sie eine 0 in der ersten Zeile, dritte Spalte (R1C3). Erstellen Sie eine 0 in der ersten Zeile, zweite Spalte (R1C2). 


Beachten Sie, dass Multiplikation und Division nur Umkehrfunktionen voneinander sind. Wir können sagen, dass wir mit 1/3 multiplizieren oder durch 3 dividieren, ohne das Ergebnis zu ändern. 
Schreiben Sie Zeile 3 (die sich nicht geändert hat) wenn R3=[1,1,1,7]. Seien Sie vorsichtig, wenn Sie negative Zahlen subtrahieren, um sicherzustellen, dass die Zeichen korrekt bleiben. Lassen Sie uns nun zuerst die Brüche in ihre unechte Form bringen. Dies erleichtert spätere Schritte der Lösung. Sie können die Brüche im letzten Schritt der Aufgabe vereinfachen. 
Beachten Sie, dass, wenn die linke Hälfte der Folge wie die Lösung mit 0 und 1 aussieht, die rechte Hälfte mit unechten Brüchen hässlich aussehen kann. Lass sie einfach so, wie sie jetzt sind. Denken Sie daran, die nicht betroffenen Zeilen weiter zu kopieren, also R1=[1,1/3,-1/3,3] und R3=[1,1,1,7]. 
Weiter entlang R1=[1.1/3,-1/3.3] und R2=[0.1,-5/8.27/8] kopieren. Denken Sie daran, dass Sie immer nur eine Zeile ändern. 

Beachten Sie, dass die Brüche, die im vorherigen Schritt ziemlich kompliziert erschienen, bereits beginnen, sich aufzulösen. Weiter mit R1=[1.1/3,-1/3.3] und R2=[0.1,-5/8.27/8]. Beachten Sie, dass Sie an dieser Stelle die Diagonale von Einsen für Ihre Lösungsmatrix haben. Sie müssen nur drei Elemente der Matrix in 0 umwandeln, um Ihre Lösung zu finden. 
Dann nimm R1=[1,1/3,-1/3,3] und R3=[0,0,1,1]. 
Nimm das unveränderte R2=[0,1,0,4] und R3=[0,0,1,1]. 

1002 0104 0011 


Da sich jede Gleichung zu einer echten mathematischen Aussage vereinfacht, sind Ihre Lösungen korrekt. Wenn eine der Lösungen nicht korrekt ist, überprüfen Sie Ihre Arbeit erneut und suchen Sie nach Fehlern. Einige häufige Fehler treten auf, wenn man Minuszeichen auf dem Weg loswird oder wenn man die Multiplikation und Addition von Brüchen verwechselt. 
Matrizen lösen
Eine Matrix ist eine sehr nützliche Methode, um Zahlen in einem Blockformat darzustellen, mit der Sie dann ein System linearer Gleichungen lösen können. Wenn Sie nur zwei Variablen haben, werden Sie wahrscheinlich eine andere Methode verwenden. Lesen Sie darüber in Lösen eines Gleichungssystems für Beispiele dieser anderen Methoden. Aber wenn Sie drei oder mehr Variablen haben, ist eine Matrix ideal. Durch wiederholte Kombinationen von Multiplikation und Addition können Sie systematisch zu einer Lösung gelangen.
Schritte
Teil 1 von 4: Erstellen der Matrix

1. Stellen Sie sicher, dass Sie über genügend Daten verfügen. Um eine eindeutige Lösung für jede Variable in einem linearen System mit einer Matrix zu erhalten, müssen Sie so viele Gleichungen haben, wie Sie Variablen lösen möchten. Zum Beispiel: mit den Variablen x, y und z braucht man drei Gleichungen. Wenn Sie vier Variablen haben, benötigen Sie vier Gleichungen.
- Wenn Sie weniger Gleichungen haben als die Anzahl der Variablen, werden Sie einige Grenzen der Variablen lernen (z. B. x = 3y und y = 2z), aber Sie werden keine genaue Lösung erhalten. Für diesen Artikel werden wir nur auf eine einzigartige Lösung hinarbeiten.

2. Schreiben Sie Ihre Gleichungen in Standardform. Bevor Sie Daten aus den Gleichungen in eine Matrixform gießen können, schreiben Sie zuerst jede Gleichung in Standardform. Die Standardform für eine lineare Gleichung ist Ax+By+Cz=D, wobei die Großbuchstaben die Koeffizienten (Zahlen) sind und die letzte Zahl (in diesem Beispiel das D) rechts vom Gleichheitszeichen steht.

3. Platziere die Zahlen aus dem Gleichungssystem in einer Matrix. Eine Matrix ist eine Gruppe von Zahlen, die in einer Art Tabelle angeordnet sind, mit der wir arbeiten werden, um das System zu lösen. Es enthält im Grunde die gleichen Daten wie die Gleichungen selbst, jedoch in einem einfacheren Format. Um die Matrix Ihrer Gleichungen in Standardform zu erstellen, kopieren Sie einfach die Koeffizienten und das Ergebnis jeder Gleichung in eine einzelne Zeile und stapeln Sie diese Zeilen übereinander.

4. Zeichne eine große eckige Klammer um deine gesamte Matrix. Konventionell wird eine Matrix durch ein Paar eckiger Klammern [ ] um den gesamten Zahlenblock bezeichnet. Die Klammern haben keinen Einfluss auf die Lösung, weisen jedoch darauf hin, dass Sie mit Matrizen arbeiten. Eine Matrix kann aus beliebig vielen Zeilen und Spalten bestehen. In diesem Artikel verwenden wir Klammern um eine Reihe von Begriffen, um anzuzeigen, dass sie zusammengehören.

5. Verwendung allgemeiner Symbolik. Beim Arbeiten mit Matrizen ist es üblich, die Zeilen mit dem Kürzel R und die Spalten mit dem Kürzel C . zu bezeichnen. Sie können zusammen mit diesen Buchstaben Zahlen verwenden, um eine bestimmte Zeile oder Spalte zu bezeichnen. Um beispielsweise Zeile 1 einer Matrix anzuzeigen, können Sie R1 . schreiben. Zeile 2 wird dann zu R2.
Teil 2 von 4: Erlernen der Operationen zum Lösen eines Systems mit einer Matrix

1. Verstehen der Form der Lösungsmatrix. Bevor Sie mit der Lösung Ihres Gleichungssystems beginnen, müssen Sie verstehen, was Sie mit der Matrix tun werden. An dieser Stelle haben Sie eine Matrix, die wie folgt aussieht:
- 31-19
- 2-21-3
- 1117
- Sie arbeiten mit einer Reihe von Grundoperationen, um die `Lösungsmatrix` zu erstellen. Die Lösungsmatrix sieht wie folgt aus:
- 100x
- 010y
- 001z
- Beachten Sie, dass die Matrix aus Einsen in einer diagonalen Linie mit Nullen in allen anderen Räumen außer der vierten Spalte besteht. Die Zahlen in der vierten Spalte sind die Lösungen für die Variablen x, y und z.

2. Verwenden Sie die Skalarmultiplikation. Das erste Werkzeug, das Ihnen zur Verfügung steht, um ein System mit einer Matrix zu lösen, ist die Skalarmultiplikation. Dies ist einfach ein Begriff, der bedeutet, dass Sie die Elemente in einer Zeile der Matrix mit einer konstanten Zahl (keine Variable) multiplizieren. Denken Sie bei der Skalarmultiplikation daran, dass Sie jeden Term der gesamten Folge mit der von Ihnen gewählten Zahl multiplizieren müssen. Wenn Sie den ersten Term vergessen und einfach multiplizieren, erhalten Sie eine falsche Lösung. Sie müssen jedoch nicht die gesamte Matrix gleichzeitig multiplizieren. Bei der Skalarmultiplikation arbeiten Sie immer nur an einer Reihe.

3. Verwenden Sie Zeilenaddition oder Zeilensubtraktion. Das zweite Werkzeug, das Sie verwenden können, ist das Addieren oder Subtrahieren von zwei Zeilen der Matrix. Um die 0-Terme in Ihrer Lösungsmatrix zu erstellen, müssen Sie Zahlen addieren oder subtrahieren, um zur 0 . zu gelangen. Wenn beispielsweise R1 einer Matrix [1,4,3,2] und R2 [1,3,5,8] ist, können Sie die erste Zeile von der zweiten Zeile subtrahieren und eine neue Zeile erstellen [ 0,-1, 2,6], weil 1-1=0 (erste Spalte), 3-4=-1 (zweite Spalte), 5-3=2 (dritte Spalte) und 8-2=6 (vierte Spalte) Säule). Wenn Sie eine Zeilenaddition oder -subtraktion durchführen, schreiben Sie Ihr neues Ergebnis neu anstelle der Zeile, mit der Sie begonnen haben. In diesem Fall würden wir Zeile 2 herausnehmen und die neue Zeile [0,-1,2,6] einfügen.

4. Kombinieren Sie Reihenaddition und Skalarmultiplikation in einem einzigen Schritt. Sie können nicht erwarten, dass die Terme immer übereinstimmen, also können Sie eine einfache Addition oder Subtraktion verwenden, um Nullen in Ihrer Matrix zu erstellen. Häufiger müssen Sie ein Vielfaches einer anderen Zeile addieren (oder subtrahieren). Führen Sie dazu zuerst die Skalarmultiplikation durch und fügen Sie dann dieses Ergebnis der Zielzeile hinzu, die Sie ändern möchten.

5. Kopieren Sie Zeilen, die während der Arbeit unverändert bleiben. Während Sie an der Matrix arbeiten, ändern Sie jeweils eine einzelne Zeile, entweder durch Skalarmultiplikation, Zeilenaddition oder Zeilensubtraktion oder durch eine Kombination von Schritten. Wenn Sie eine Zeile ändern, stellen Sie sicher, dass Sie die anderen Zeilen Ihrer Matrix in ihrer ursprünglichen Form kopieren.

6. Zuerst von oben nach unten arbeiten. Um das System zu lösen, arbeiten Sie in einem sehr organisierten Muster, im Wesentlichen "lösen" Sie jeweils einen Term der Matrix. Die Reihenfolge für ein Array mit drei Variablen sieht wie folgt aus:

7. Arbeiten Sie sich von unten nach oben zurück. Wenn Sie die Schritte richtig gemacht haben, haben Sie an dieser Stelle die Hälfte der Lösung erreicht. Sie müssen die diagonale Linie von Einsen haben, mit Nullen darunter. Die Zahlen in der vierten Spalte spielen an dieser Stelle keine Rolle. Nun arbeiten Sie sich wie folgt zurück:

8. Prüfen Sie, ob Sie die Lösungsmatrix erstellt haben. Wenn Ihre Arbeit richtig ist, haben Sie die Lösungsmatrix mit Einsen in einer diagonalen Linie von R1C1, R2C2, R3C3 und Nullen in den anderen Positionen der ersten drei Spalten erstellt. Die Zahlen in der vierten Spalte sind die Lösungen für Ihr Linearsystem.
Teil 3 von 4: Zusammenstellen der Schritte zur Lösung des Systems

1. Beginnen Sie mit einem Beispielsystem linearer Gleichungen. Um diese Schritte zu üben, beginnen wir mit dem zuvor verwendeten System: 3x+y-z=9, 2x-2y+z=-3 und x+y+z=7. Wenn Sie dies in eine Matrix schreiben, haben Sie R1= [3.1,-1,9], R2=[2,-2,1,-3] und R3=[1,1,1,7].

2. Erstellen Sie eine 1 an der ersten Position R1C1. Beachten Sie, dass R1 derzeit mit einem 3 . beginnt. Sie müssen es in 1 ändern. Sie können dies durch Skalarmultiplikation tun, indem Sie alle vier Terme von R1 mit 1/3 . multiplizieren. In Kurzschrift können Sie als R1*1/3 . schreiben. Dies ergibt ein neues Ergebnis für R1, wenn R1=[1,1/3,-1/3,3]. Übernehme R2 und R2 unverändert, wenn R2=[2,-2,1,-3] und R3=[1,1,1,7].

3. Erstellen Sie eine 0 in der zweiten Zeile, erste Spalte (R2C1). An diesem Punkt R2=[2,-2,1,-3]. Um näher an die Lösungsmatrix zu kommen, müssen Sie den ersten Term von einer 2 in eine 0 ändern. Sie können dies tun, indem Sie den doppelten Wert von R1 subtrahieren, da R1 mit einer 1 beginnt. Kurz gesagt ist die Operation R2-2*R1. Denken Sie daran, dass Sie R1 nicht ändern, sondern einfach damit arbeiten. Also zuerst R1 kopieren wenn R1=[1,1/3,-1/3,3]. Wenn Sie dann jeden Term von R1 verdoppeln, erhalten Sie 2*R1=[2,2/3,-2/3,6]. Ziehen Sie schließlich dieses Ergebnis vom ursprünglichen R2 ab, um Ihr neues R2 zu erhalten. Von Term für Term wird diese Subtraktion zu (2-2), (-2-2/3), (1-(-2/3), (-3-6). Wir vereinfachen dies auf das neue R2=[0,-8/3,5/3,-9]. Beachten Sie, dass der erste Term 0 ist (was auch immer Ihr Ziel war).

4. Erstellen Sie eine 1 in der zweiten Zeile, zweite Spalte (R2C2). Um weiterhin die diagonale Linie der Einsen zu bilden, müssen Sie den zweiten Term -8/3 in 1 . umwandeln. Tun Sie dies, indem Sie die gesamte Zeile mit dem Kehrwert dieser Zahl (-3/8) multiplizieren. Symbolisch ist dieser Schritt R2*(-3/8). Die resultierende zweite Zeile ist R2=[0,1,-5/8,27/8].

5. Erstellen Sie eine 0 in der dritten Zeile, erste Spalte (R3C1). Ihr Fokus bewegt sich jetzt in die dritte Reihe, R3=[1,1,1,7]. Um eine 0 an der ersten Position zu machen, müssen Sie eine 1 von der 1 subtrahieren, die sich gerade an dieser Position befindet. Wenn Sie nach oben schauen, steht eine 1 an der ersten Stelle von R1. Sie müssen also nur R1 von R3 subtrahieren, um das gewünschte Ergebnis zu erhalten. Arbeitshalbjahr wird daraus (1-1), (1-1/3), (1-(-1/3)), (7-3). Diese vier Miniprobleme können dann auf das neue R3=[0.2/3.4/3.4] vereinfacht werden.

6. Machen Sie eine 0 in der dritten Zeile, zweite Spalte (R3C2). Dieser Wert beträgt derzeit 2/3, muss aber in 0 . umgewandelt werden. Auf den ersten Blick sieht es so aus, als ob Sie die R1-Werte doppelt subtrahieren können, da die entsprechende Spalte von R1 ein 1/3 . enthält. Wenn Sie jedoch alle Werte von R1 verdoppeln und subtrahieren, ändert sich die 0 in der ersten Spalte von R3, was Sie nicht möchten. Dies wäre ein Rückschritt in Ihrer Lösung. Sie müssen also mit einer Kombination von R2 arbeiten. Wenn Sie 2/3 von R2 subtrahieren, erstellen Sie eine 0 in der zweiten Spalte, ohne die erste Spalte zu ändern. In abgekürzter Form ist dies R3- 2/3*R2. Die einzelnen Terme werden (0-0), (2/3-2/3), (4/3-(-5/3*2/3)), (4-27/8*2/3). Die Vereinfachung ergibt dann R3=[0,0,42/24.42/24].

7. Erstellen Sie eine 1 in der dritten Zeile, dritte Spalte (R3C3). Dies ist eine einfache Multiplikation mit dem Kehrwert der angegebenen Zahl. Der aktuelle Wert ist 42/24, Sie können also mit 24/42 multiplizieren, um den gewünschten Wert von 1 . zu erhalten. Beachten Sie, dass die ersten beiden Terme beide 0 sind, also bleibt jede Multiplikation 0. Der neue Wert von R3=[0,0,1,1].

8. Erstellen Sie eine 0 in der zweiten Zeile, dritten Spalte. R2 ist derzeit [0,1,-5/8,27/8], mit einem Wert von -5/8 in der dritten Spalte. Sie müssen es in eine 0 umwandeln. Dies bedeutet, dass Sie mit R3 eine Operation ausführen müssen, die darin besteht, 5/8 . hinzuzufügen. Da die entsprechende dritte Spalte von R3 eine 1 ist, müssen Sie alle Werte von R3 mit 5/8 multiplizieren und das Ergebnis zu R2 addieren. Kurz gesagt ist dies R2+5/8*R3. Term für Term ist dies R2=(0+0), (1+0), (-5/8+5/8), (27/8+5/8). Dies kann vereinfacht werden zu R2=[0,1,0,4].

9. Erstellen Sie eine 0 in der ersten Zeile, dritte Spalte (R1C3). Die erste Zeile ist derzeit R1=[1.1/3,-1/3.3]. Sie müssen das -1/3 in der dritten Spalte in eine 0 umwandeln, indem Sie eine Kombination von R3 verwenden. Sie möchten R2 nicht verwenden, da die 1 in der zweiten Spalte von R2 R1 falsch modifizieren würde. Also multipliziert man R3*1/3 und addiert das Ergebnis zu R1. Die Notation dafür ist R1+1/3*R3. Die Term-für-Term-Berechnung ergibt R1=(1+0), (1/3+0), (-1/3+1/3), (3+1/3). Sie können dies zu einem neuen R1=[1,1/3,0,10/3] vereinfachen.

10. Machen Sie eine 0 in der ersten Zeile, zweite Spalte (R1C2). Wenn alles richtig gemacht ist, sollte dies der letzte Schritt sein. Sie müssen das 1/3 in der zweiten Spalte in eine 0 umwandeln. Sie können dies erhalten, indem Sie R2 * 1/3 . multiplizieren und subtrahieren. Kurz gesagt ist dies R1-1/3*R2. Das Ergebnis ist R1=(1-0), (1/3-1/3), (0-0), (10/3-4/3). Vereinfachen ergibt dann R1=[1,0,0,2].

11. Suche nach der Lösungsmatrix. An diesem Punkt, wenn alles gut ging, hätten Sie die drei Zeilen R1=[1,0,0,2], R2=[0,1,0,4] und R3=[0,0,1,1] haben müssen. Beachten Sie, dass Sie, wenn Sie dies in Blockmatrixform mit den Zeilen übereinander schreiben, diagonale Einsen mit Nullen weiter unten haben und Ihre Lösungen in der vierten Spalte stehen. Die Lösungsmatrix sollte wie folgt aussehen:

12. Verstehen Sie Ihre Lösung. Nachdem Sie die linearen Gleichungen in eine Matrix umgewandelt haben, geben Sie die x-Koeffizienten in die erste Spalte, die y-Koeffizienten in die zweite Spalte, die z-Koeffizienten in die dritte Spalte ein. Wenn Sie nun die Matrix in Gleichungen umschreiben wollen, bedeuten diese drei Zeilen der Matrix eigentlich die drei Gleichungen 1x+0y+0z=2, 0x+1y+0z=4 und 0x+0y+1z=1. Da wir die 0-Terme durchstreichen können und die 1-Koeffizienten nicht schreiben müssen, vereinfachen sich diese drei Gleichungen zur Lösung x=2, y=4 und z=1. Dies ist die Lösung Ihres linearen Gleichungssystems.
Teil 4 von 4: Überprüfen Sie Ihre Lösung

1. Verarbeite die Lösungen in jeder Variablen in jeder Gleichung. Es ist immer eine gute Idee zu überprüfen, ob Ihre Lösung tatsächlich richtig ist. Sie tun dies, indem Sie Ihre Ergebnisse in den ursprünglichen Gleichungen testen.
- Die ursprünglichen Gleichungen für dieses Problem waren: 3x+y-z=9, 2x-2y+z=-3 und x+y+z=7. Wenn Sie die Variablen durch ihre gefundenen Werte ersetzen, erhalten Sie 3*2+4-1=9, 2*2-2*4+1=-3 und 2+4+1=7.

2. Vereinfache eine beliebige Gleichung. Führen Sie die Operationen in jeder Gleichung gemäß den grundlegenden Operationsregeln aus. Die erste Gleichung vereinfacht sich zu 6+4-1=9 oder 9=9. Die zweite Gleichung kann vereinfacht werden zu 4-8+1=-3 oder -3=-3. Die letzte Gleichung ist einfach 7=7.

3. Schreiben Sie Ihre endgültigen Lösungen auf. Für dieses gegebene Problem lautet die endgültige Lösung x=2, y=4 und z=1.
Tipps
- Wenn Ihr Gleichungssystem sehr komplex ist und viele Variablen enthält, möchten Sie vielleicht einen Grafikrechner verwenden, anstatt die Arbeit von Hand zu erledigen. Für Informationen dazu kannst du auch wikiHow konsultieren.
Оцените, пожалуйста статью