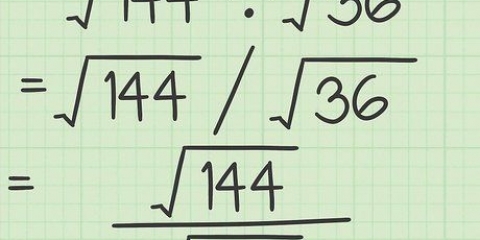Ein weiteres Beispiel: Wir wollen die Quadratwurzel von 25 (√(25)). Das bedeutet, dass wir die Zahl finden müssen, die mit sich selbst multipliziert 25 als Produkt ergibt. Da 5 = 5 × 5 = 25, können wir sagen, dass √(25) = 5. Sie können sich dies auch als "Rückgängigmachen" eines Quadrats (oder einer Potenzzahl) vorstellen. Wenn wir zum Beispiel die Quadratwurzel von 64 (√64) finden wollen, betrachten wir 64 als 8. zuerst. Da ein Radikal im Prinzip ein Quadrat `eliminiert`, können wir sagen, dass √(64) = √(8) = 8. 
Zahlen, die nach der Quadratwurzel keine ganzen Zahlen ergeben, heißen dagegen, unvollkommenes Quadrat. Wenn Sie die Quadratwurzel einer dieser Zahlen ziehen, erhalten Sie normalerweise eine Dezimalzahl oder einen Bruch. Manchmal können die Dezimalstellen wirklich unordentlich werden. Zum Beispiel √(13) = 3.605551275464… 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Angenommen, Sie möchten die Quadratwurzel von 900 . berechnen. Auf den ersten Blick sieht das sehr schwierig aus! Es ist jedoch nicht schwer, wenn wir 900 faktorisieren. `Faktoren` sind die Zahlen, die sich miteinander multiplizieren können, um eine andere Zahl zu ergeben. Da beispielsweise 6 das Produkt von 1 × 6 und 2 × 3 ist, sind die Faktoren von 6 die Zahlen 1, 2, 3 und 6. Anstatt mit der Zahl 900 zu rechnen, was etwas umständlich ist, schreiben wir es als 9 × 100. Da 9 ein perfektes Quadrat ist und von 100 getrennt ist, können wir seine Quadratwurzel ziehen. (9 × 100) = √(9) × √(100) = 3 × √(100). Mit anderen Worten, √(900) = 3√(100). Wir können diese beiden Schritte noch weiter vereinfachen, indem wir 100 in die Faktoren 25 und 4 teilen. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Wir können also sagen, dass √(900) = 3(10) = 30. 
Hinweis: Obwohl imaginäre Zahlen nicht mit regulären Zahlen dargestellt werden können, können sie dennoch in vielerlei Hinsicht als reguläre Zahlen behandelt werden. Zum Beispiel können die Wurzeln negativer Zahlen quadriert werden, um diese negativen Zahlen wie jede andere Quadratwurzel zu erhalten. Zum Beispiel: ich = -1. 

In unserem Beispiel teilen wir 6,45 in Paare wie folgt auf: 6-,45-00. Beachten Sie, dass sich links eine `verbleibende` Zahl befindet &mdash das ist der Punkt. 
In unserem Beispiel ist die erste Gruppe in 6-,45-00 die 6. Die größte Zahl kleiner oder gleich 6 ist 2 — 2 = 4. Schreibe eine `2` über die 6 unter dem Radikal. 
In unserem Beispiel beginnen wir mit dem Doppelten von 2, der ersten Ziffer unserer Antwort. 2 × 2 = 4. Dann subtrahieren wir 4 von 6 (unsere erste `Gruppe`) und erhalten 2 als Antwort. Dann verschieben wir die nächste Gruppe (45) eine Zeile nach unten, um 245 . zu erhalten. Schließlich schreiben wir links eine weitere 4 und lassen am Ende etwas Platz zum Hinzufügen, wie folgt: 4_. 
In unserem Beispiel suchen wir nach der Zahl, um die Lücke in 4_ × _ auszufüllen; das macht die Antwort so groß wie möglich, aber immer noch kleiner oder gleich 245. In diesem Fall lautet die Antwort 5. 45 × 5 = 225, während 46 × 6 = 276. 
Wir fahren mit unserem Beispiel fort und fahren fort mit 225 - 245 = 20. Dann bringen wir das nächste Ziffernpaar 00 herunter, um 2000 . zu erhalten. Wenn wir die Zahl über dem Radikal verdoppeln, erhalten wir 25 × 2 = 50. Wir lösen das Unbekannte in 50_ × _ =/< 2000, dann bekommen wir 3 als antwort. An dieser Stelle haben wir `253` über dem Radikal — wiederholen wir dies noch einmal, 9 ist die nächste Ziffer. 
In unserem Beispiel ist die Zahl unter dem Wurzelzeichen 6.45, also verschieben wir einfach den Dezimalpunkt nach oben und platzieren ihn zwischen 2 und 5 unserer Antwort, was uns ergibt 2.539 ergibt. 

In unserem Beispielproblem ist eine vernünftige Schätzung für die Quadratwurzel von 40 vielleicht 6.4, denn aus dem Obigen wissen wir, dass die Antwort wahrscheinlich etwas näher bei 6 liegt als bei 7. 
Multiplizieren Sie 6,4 mit sich selbst, also 6,4 × 6,4 = 40,96, die etwas größer ist als die ursprüngliche Zahl. Dann multiplizieren wir die Zahl mit einem Zehntel kleiner als unsere Schätzung oben (da unsere Antwort zu hoch war), und wir erhalten 6,3 × 6,3 = 39.69. Dies ist etwas niedriger als unsere ursprüngliche Zahl. Das bedeutet, dass die Quadratwurzel von 40 irgendwo liegt zwischen 6,3 und 6,4 Lügen. Da 39,69 näher an 40 als 40,96 liegt, wissen Sie auch, dass die Quadratwurzel näher an 6,3 als an 6,4 liegt. 
In unserem Beispiel wählen wir 6,33 für unsere Schätzung in zwei Dezimalstellen. Quadrat 6,33 und Sie erhalten 6,33 × 6,33 = 40,0689. Da dies etwas über unserer ursprünglichen Zahl liegt, versuchen wir es mit einer etwas niedrigeren Zahl, z. B. 6,32. 6,32 × 6,32 = 39,9424. Dies liegt etwas unter unserer ursprünglichen Zahl, daher wissen wir, dass die genaue Quadratwurzel zwischen 6.33 und 6.32 Lügen. Wenn wir noch weiter gehen wollten, können wir weiterhin den gleichen Ansatz verwenden, um eine immer genauere Antwort zu erhalten.
Quadratwurzeln lösen
Während der einschüchternde Anblick eines Quadratwurzelsymbols Menschen mit Matheangst erschrecken kann, sind Quadratwurzelprobleme nicht so schwer zu lösen, wie sie auf den ersten Blick erscheinen. Einfache Quadratwurzelprobleme lassen sich oft genauso leicht lösen wie einfache Multiplikations- und Divisionsprobleme. Komplexere Wurzelprobleme hingegen erfordern möglicherweise etwas mehr Arbeit, aber mit der richtigen Vorgehensweise lassen sich auch diese Probleme leicht lösen. Beginnen Sie noch heute mit dem Üben von Quadratwurzelproblemen, um diese mathematische Fähigkeit zu erlernen, die für Sie möglicherweise neu ist!
Schritte
Teil 1 von 3: Kräfte und Wurzeln verstehen

1. Quadrieren Sie eine Zahl, indem Sie sie mit sich selbst multiplizieren. Um Wurzeln zu verstehen, beginnen Sie am besten mit den Quadraten. Quadrate sind einfach – das Quadrieren einer Zahl entspricht der Multiplikation mit sich selbst. Zum Beispiel: 3 zum Quadrat ist gleich 3 × 3 = 9, und 9 zum Quadrat ist gleich 9 × 9 = 81. Quadrate werden durch eine kleine "2" über und rechts von der Zahl im Quadrat angezeigt — wie folgt: 3, 9, 100 usw.
- Versuchen Sie, einige Zahlen selbst zu quadrieren, um dieses Konzept zu testen. Denken Sie daran, dass das Quadrieren einer Zahl nichts anderes ist, als diese Zahl mit sich selbst zu multiplizieren. Das geht auch mit negativen Zahlen. In jedem Fall wird die Antwort immer positiv sein. Zum Beispiel: -8 = -8 × -8 = 64.

2. Um die Wurzel einer Zahl zu finden, finde die `Inverse` eines Quadrats. Das Symbol der Quadratwurzel (√, auch als `Radikalzeichen` bekannt) ist im Grunde das `Gegenstück` des Quadratsymbols (). Wenn Sie ein Wurzelzeichen sehen, können Sie sich fragen: „Welche Zahl kann ich mit sich selbst multiplizieren, damit ich die Zahl unter dem Wurzelzeichen bekomme??` Beispiel: Wenn Sie die Quadratwurzel √(9) sehen, dann suchen Sie die Zahl, die mit sich selbst multipliziert neun als Produkt hat. In diesem Fall ist das drei, weil 3 = 9.

3. Kenne den Unterschied zwischen perfekten und unvollkommenen Quadraten. Bisher waren die Antworten auf die Quadratwurzelprobleme schöne, runde Zahlen. Dies ist nicht immer der Fall – tatsächlich gibt es Antworten auf Quadratwurzeln, die sehr lange, unangenehme Dezimalzahlen sind. Wurzelzahlen, die ganze Zahlen sind (mit anderen Worten, Zahlen, die keine Brüche oder Dezimalzahlen sind) heißen Quadrate. Alle obigen Beispiele (9, 25 und 64) sind Quadrate (auch perfekte Quadrate genannt), weil wir durch das Ziehen von Quadratwurzeln ganze Zahlen (3, 5 und 8) als Ergebnis erhalten.

4. Merken Sie sich die ersten 10-12 Quadrate. Wie Sie wahrscheinlich bemerkt haben, sind Quadratwurzeln oder Quadrate oft sehr einfach! Da diese mathematischen Aufgaben so einfach sind, lohnt es sich, die Wurzeln der ersten 12 oder mehr Quadrate zu lernen. Diese Zahlen werden Ihnen häufig begegnen, sodass Sie auf lange Sicht viel Zeit sparen können, indem Sie sie früh lernen. Die ersten 12 Quadrate sind:

5. Vereinfachen Sie Wurzeln, indem Sie nach Möglichkeit Quadrate entfernen. Das Finden der Wurzeln unvollkommener Quadrate kann manchmal schwierig sein – insbesondere, wenn Sie keinen Taschenrechner verwenden (die folgenden Absätze geben Ihnen Tricks, um diesen Vorgang zu vereinfachen). Es ist jedoch oft möglich, die Zahlen unter dem Radikalzeichen zu vereinfachen, um das Arbeiten mit ihnen zu erleichtern. Um dies zu tun, müssen Sie nur die Zahl unter dem Wurzelsatz faktorisieren, dann die Quadratwurzel von Faktoren ziehen, die Quadrate sind, und die Antwort außerhalb des Wurzelsatzes schreiben. Das ist einfacher als es klingt – lesen Sie weiter, um mehr zu erfahren!

6. Verwenden Sie imaginäre Zahlen für die Wurzeln negativer Zahlen. Welches Quadrat ist -16? Es ist nicht 4 oder -4 – das Quadrieren beider ergibt 16 (positiv). Weißt du nicht? Tatsächlich gibt es keine Möglichkeit, die Quadratwurzel von -16 oder eine negative Zahl mit regulären Zahlen zu schreiben. In diesen Fällen müssen wir imaginäre Zahlen (normalerweise in Form von Buchstaben oder Symbolen) verwenden, um die Quadratwurzel der negativen Zahl zu ersetzen. Zum Beispiel wird die Variable `i` normalerweise für die Quadratwurzel von -1 . verwendet. Als allgemeine Regel gilt, dass die Quadratwurzel einer negativen Zahl immer eine imaginäre Zahl ist (oder eine enthält).
Teil 2 von 3: Verwenden von langen Divisionsalgorithmen

1. Ordne dein Quadratwurzelproblem wie lange Division. Obwohl es etwas zeitaufwändig sein kann, ist es möglich, die Wurzeln von schwierigen unvollkommenen Quadraten ohne Taschenrechner zu berechnen. Dazu verwenden wir eine Lösungsmethode (oder Algorithmus), die ähnlich – aber nicht genau gleich – ist eine lange Division.
- Schreiben Sie zuerst die Quadratwurzel auf die gleiche Weise wie bei der langen Division. Nehmen wir zum Beispiel an, wir wollen die Quadratwurzel von 6,45 berechnen, was sicherlich kein bequemes perfektes Quadrat ist. Zuerst schreiben wir ein gewöhnliches Wurzelsymbol (√), dann schreiben wir die Zahl darunter. Dann zeichnen wir eine Linie über der Zahl, so dass sie in einem kleinen Kästchen steht – genau wie bei der langen Division. Als wir fertig sind, haben wir ein verlängertes `√` mit 6,45 darunter notiert.
- Wir schreiben Zahlen über das Problem, also lass etwas Platz.

2. Gruppiere die Zahlen paarweise. Um Ihr Problem zu lösen, gruppieren Sie die Ziffern der Zahl unter dem Wurzelzeichen paarweise, beginnend mit dem Komma. Sie können kleine Hervorhebungen hinzufügen (z. B. Punkte, Schrägstriche, Kommas usw.).) zwischen deinen Paaren, um sie voneinander zu unterscheiden.

3. Finden Sie die größte Zahl, deren Quadrat kleiner oder gleich der ersten `Gruppe` ist. Beginnen Sie mit der ersten Zahl oder dem ersten Paar auf der linken Seite. Wählen Sie die größte Zahl mit einem Quadrat, das kleiner oder gleich der `Gruppe` ist. Wenn die Gruppe beispielsweise 37 ist, würden Sie die 6 auswählen, da 6 = 36 (weniger als 37), aber 7 = 49 (größer als 37). Schreiben Sie diese Zahl über die erste Gruppe. Dies ist die erste Ziffer Ihrer Antwort.

4. Verdoppeln Sie die Zahl, die Sie gerade aufgeschrieben haben, schreiben Sie sie unter die erste Gruppe und ziehen Sie sie ab. Nimm die erste Ziffer deiner Antwort (die Zahl, die du gerade gefunden hast) und verdopple sie. Schreibe dies unter deine erste Gruppe und ziehe sie ab, um den Unterschied zu finden. Platziere das nächste Zahlenpaar neben der Antwort unten. Schreiben Sie zum Schluss die letzte Ziffer des Doppelten der ersten Ziffer Ihrer Antwort auf die linke Seite und lassen Sie daneben etwas Platz.

5. Fülle den leeren Raum. Als nächstes möchten Sie rechts neben der Zahl, die Sie links geschrieben haben, eine Ziffer hinzufügen. Wählen Sie eine Zahl, die mit Ihrer neuen Zahl multipliziert wird, um das größtmögliche Produkt zu erhalten, die jedoch kleiner oder gleich der "heruntergezogenen" Zahl ist. Wenn Ihre „heruntergebrachte“ Zahl beispielsweise 1700 ist und die Zahl links davon 40_, würden Sie die Lücke mit „404“ ausfüllen, da 404 × 4 = 1616 (weniger als 1700) ist, während 405 × 5 = 2025. Die Zahl, die Sie in diesem Schritt finden, ist die zweite Ziffer Ihrer Antwort, sodass Sie sie über dem Radikal hinzufügen können.

6. Verwenden Sie weiterhin Ihre `leeren` Zahlen für Ihre Antwort. Fahren Sie mit dieser modifizierten langen Division fort, bis Sie Nullen erhalten, wenn Sie die `Drawdown`-Zahl subtrahieren, oder Sie die gewünschte Genauigkeit erreicht haben. Wenn Sie fertig sind, sind die Zahlen, die Sie bei jedem Schritt zum Ausfüllen der Lücken verwendet haben (plus die allererste Zahl, die Sie verwendet haben), die Ziffern Ihrer Antwort.

7. Verschiebe den Dezimalpunkt deines ursprünglichen `Teilers` nach oben. Um Ihre Antwort abzurunden, müssen Sie das Komma (das Komma) an der richtigen Stelle einsetzen. Glücklicherweise ist dies einfach – alles, was Sie tun müssen, ist, es mit dem Dezimalpunkt in Ihrer ursprünglichen Zahl auszurichten. Wenn die Zahl unter dem Radikal 49,8 beträgt, verschieben Sie den Dezimalpunkt zwischen den beiden Zahlen über 9 und 8 . nach oben.
Teil 3 von 3: Unvollkommene Quadrate schnell schätzen

1. Finden Sie unvollkommene Quadrate durch Schätzen. Sobald du dir deine Quadrate auswendig gelernt hast, wird es viel einfacher, die Wurzeln von unvollkommenen Quadraten zu finden. Da Sie bereits ein Dutzend Quadrate kennen, können Sie jede Zahl, die zwischen zwei dieser perfekten Quadrate liegt, durch Schätzung zwischen diesen Werten ermitteln. Finde zunächst die beiden Quadrate, zwischen denen deine Zahl liegt. Bestimmen Sie dann, welches dieser beiden Quadrate der Zahl am nächsten kommt.
- Nehmen wir zum Beispiel an, wir müssen die Quadratwurzel von 40 . finden. Da wir unsere Quadrate auswendig gelernt haben, können wir sagen, dass 40 zwischen 6 und 7 oder 36 und 49 liegt. Da 40 größer als 6 ist, ist seine Quadratwurzel größer als 6, und da sie kleiner als 7 ist, ist seine Quadratwurzel kleiner als 7. Die Zahl 40 liegt etwas näher bei 36 als bei 49, daher wird die Antwort wahrscheinlich etwas näher bei 6 liegen. In den nächsten Schritten werden wir unsere Antwort genauer machen.

2. Schätzen Sie die Quadratwurzel auf eine Dezimalstelle. Sobald Sie zwei Quadrate ausgewählt haben, zwischen denen Ihre Zahl liegt, müssen Sie nur noch schätzen, bis Sie eine Antwort finden, mit der Sie zufrieden sind. Je weiter Sie gehen, desto genauer ist Ihre Antwort. Wählen Sie zunächst eine Zehn für Ihre Antwort aus – sie muss nicht richtig sein, aber Sie sparen Zeit, wenn Sie Ihren gesunden Menschenverstand verwenden, indem Sie eine Zahl wählen, die der richtigen Antwort nahe kommt.

3. Multiplizieren Sie die Schätzung mit sich selbst. Dann quadrieren Sie die Schätzung. Wenn Sie kein Glück haben, erhalten Sie wahrscheinlich nicht Ihre ursprüngliche Nummer - Sie werden entweder etwas höher oder niedriger enden. Wenn Ihre Antwort zu hoch ist, versuchen Sie es erneut mit einer etwas kleineren Schätzung (und umgekehrt, wenn sie zu niedrig ist).

4. Bei Bedarf weiter schätzen. Wenn Sie mit Ihren Antworten zufrieden sind, möchten Sie vielleicht einfach eine Ihrer ersten Vermutungen verwenden. Wenn Sie jedoch eine genauere Antwort wünschen, müssen Sie nur eine Schätzung für Ihr "Hundertstel" auswählen, die diese Schätzung zwischen Ihren ersten beiden liegt. Wenn Sie mit diesem Muster fortfahren, können Sie eine Antwort mit drei, vier oder mehr Dezimalstellen erhalten – es hängt nur davon ab, wie weit Sie gehen möchten.
Tipps
- Verwenden Sie für schnelle Lösungen einen Taschenrechner. Die meisten modernen Taschenrechner können Quadratwurzeln direkt berechnen. Normalerweise müssen Sie nur Ihre Zahl eingeben und dann den Knopf mit dem Radikal der zweiten Potenz (der Quadratwurzel) drücken. Um zum Beispiel die Quadratwurzel von 841 zu finden, drücken Sie die folgenden Tasten: 8, 4, 1, (√) und machen Sie es richtig 29 auf als antwort.
Оцените, пожалуйста статью