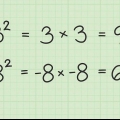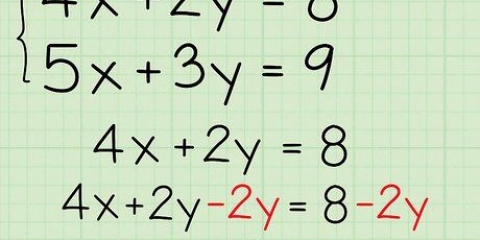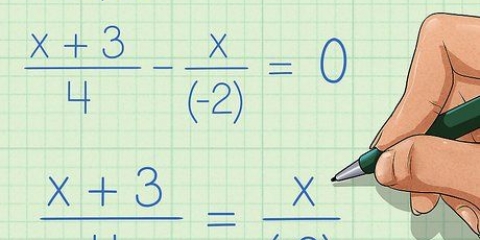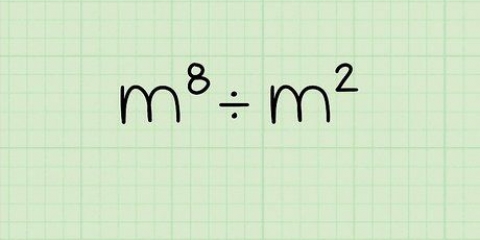Zehn hoch drei











Wie hier gezeigt, können Sie die Basis mit dem Produkt jedes der ersten Zahlenpaare multiplizieren, bis Sie die endgültige Antwort erhalten. Multiplizieren Sie einfach die ersten beiden Zahlen weiter und multiplizieren Sie dann diese Antwort mit der nächsten Zahl in der Folge. Dies gilt für jeden Exponenten. Wenn Sie mit dem Beispiel fertig sind, erhalten Sie  .
. 




Verwenden Sie eine Suchmaschine wie Startpage, Duckduckgo oder Google, um die Antwort zu finden. Sie können die `^`-Taste auf Ihrem Computer, Tablet oder Smartphone verwenden, um den Ausdruck in das Suchfeld einzugeben, und Sie sehen sofort die Antwort und Vorschläge für ähnliche Ausdrücke zum Erkunden (Duckduckgo zeigt sogar einen vollständigen Taschenrechner). 





Da alles dieselbe Zahl ist, aber multipliziert, können wir diese kombinieren: 




Da die Basen gleich sind, können Sie sie einfach zusammenzählen: 




Wie Sie gleich sehen werden, kann jede Zahl, die Teil eines Bruchs ist, wie z  , umgeschrieben werden als
, umgeschrieben werden als  . Negative Exponenten bilden Brüche.
. Negative Exponenten bilden Brüche. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Denken Sie daran, dass eine Zahl ohne Potenz einen Exponenten von 1 . hat
Denken Sie daran, dass eine Zahl ohne Potenz einen Exponenten von 1 . hat =
= 
 =
= 




![Exponenten lösen x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Exponenten lösen ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Exponenten lösen
Exponenten werden verwendet, wenn eine Zahl mit sich selbst multipliziert wird. Anstatt 



Schritte
Methode 1 von 3: Einfache Exponenten lösen

1. Lerne die richtigen Begriffe und Vokabeln für exponentielle Probleme. Hast du einen Exponenten wie  , dann arbeitest du mit zwei einfachen Teilen. Die Fahrgestellnummer ist hier eine 2, oder die Base. Diese Zahl wird mit 3 potenziert, auch bekannt als Exponent oder Energie. Reden wir über
, dann arbeitest du mit zwei einfachen Teilen. Die Fahrgestellnummer ist hier eine 2, oder die Base. Diese Zahl wird mit 3 potenziert, auch bekannt als Exponent oder Energie. Reden wir über  , dann sagen wir „zwei hoch“, „zwei hoch“ oder „zwei erhöht“.`
, dann sagen wir „zwei hoch“, „zwei hoch“ oder „zwei erhöht“.`
 , dann arbeitest du mit zwei einfachen Teilen. Die Fahrgestellnummer ist hier eine 2, oder die Base. Diese Zahl wird mit 3 potenziert, auch bekannt als Exponent oder Energie. Reden wir über
, dann arbeitest du mit zwei einfachen Teilen. Die Fahrgestellnummer ist hier eine 2, oder die Base. Diese Zahl wird mit 3 potenziert, auch bekannt als Exponent oder Energie. Reden wir über  , dann sagen wir „zwei hoch“, „zwei hoch“ oder „zwei erhöht“.`
, dann sagen wir „zwei hoch“, „zwei hoch“ oder „zwei erhöht“.` - Wenn eine Zahl mit der zweiten Potenz erhöht wird, wie z
, dann kannst du auch sagen, dass die nummer ist kariert ist, wie "fünf zum Quadrat".`
- Wenn eine Zahl mit der dritten Potenz erhöht wird, wie z
, dann kannst du diese Zahl auch a sagen Würfelzahl ist.
- Wird eine Zahl ohne Exponenten genannt, wie zum Beispiel 4, dann steht sie theoretisch in erster Potenz und kann umgeschrieben werden als
.
- Wenn der Exponent gleich 0 ist und eine `Zahl (nicht Null)` auf die `Null-Potenz` erhöht wird, dann ist die ganze Zahl gleich 1, da
oder sogar so ähnlich
Mehr dazu in der Rubrik `Tipps`.

2. Multiplizieren Sie die Basis so oft mit sich selbst, wie durch den Exponenten angegeben. Wenn Sie eine Potenz von Hand lösen müssen, schreiben Sie sie zunächst als Multiplikation um. Sie multiplizieren die Basis so oft mit sich selbst, wie durch den Exponenten angegeben. So hast du  dann multiplizierst du drei vier mal mit sich selbst
dann multiplizierst du drei vier mal mit sich selbst  . Ein paar weitere Beispiele sind:
. Ein paar weitere Beispiele sind:
 dann multiplizierst du drei vier mal mit sich selbst
dann multiplizierst du drei vier mal mit sich selbst  . Ein paar weitere Beispiele sind:
. Ein paar weitere Beispiele sind:



3. Einen Ausdruck lösen: Multiplizieren Sie die ersten beiden Zahlen miteinander, um das Produkt zu erhalten. Zum Beispiel mit  , fängst du damit an
, fängst du damit an  Das scheint eine mühsame Aufgabe zu sein, aber mach es einfach Schritt für Schritt. Beginnen Sie mit der Multiplikation der ersten beiden Vieren. Ersetzen Sie dann die beiden Vieren durch die unten gezeigte Antwort:
Das scheint eine mühsame Aufgabe zu sein, aber mach es einfach Schritt für Schritt. Beginnen Sie mit der Multiplikation der ersten beiden Vieren. Ersetzen Sie dann die beiden Vieren durch die unten gezeigte Antwort:
 , fängst du damit an
, fängst du damit an  Das scheint eine mühsame Aufgabe zu sein, aber mach es einfach Schritt für Schritt. Beginnen Sie mit der Multiplikation der ersten beiden Vieren. Ersetzen Sie dann die beiden Vieren durch die unten gezeigte Antwort:
Das scheint eine mühsame Aufgabe zu sein, aber mach es einfach Schritt für Schritt. Beginnen Sie mit der Multiplikation der ersten beiden Vieren. Ersetzen Sie dann die beiden Vieren durch die unten gezeigte Antwort:



4. Multiplizieren Sie die Antwort des ersten Paares (16) mit der nächsten Zahl. Multiplizieren Sie die Zahlen weiter, um Ihren Exponenten zu "wachsen". In Fortsetzung unseres Beispiels multiplizieren wir 16 mit den nächsten 4, sodass:






 .
.
5. Probieren Sie auch die folgenden Beispiele aus und überprüfen Sie Ihre Antworten mit einem Taschenrechner.




6. Verwenden Sie das `exp``x n  ` oder `^`-Taste Ihres Rechners für die Exponenten. Es ist fast unmöglich, größere Exponenten zu finden, wie z
` oder `^`-Taste Ihres Rechners für die Exponenten. Es ist fast unmöglich, größere Exponenten zu finden, wie z  von Hand, aber Taschenrechner können das problemlos handhaben. Der Button dafür ist meist deutlich genug gekennzeichnet. Der Windows-Rechner kann zu einem wissenschaftlichen Rechner erweitert werden, indem Sie auf die Registerkarte "Ansicht" des Rechners klicken und "Wissenschaftlich" auswählen. Wenn Sie den Standardrechner wiederherstellen möchten, klicken Sie erneut auf "Ansicht" und wählen Sie "Standard".
von Hand, aber Taschenrechner können das problemlos handhaben. Der Button dafür ist meist deutlich genug gekennzeichnet. Der Windows-Rechner kann zu einem wissenschaftlichen Rechner erweitert werden, indem Sie auf die Registerkarte "Ansicht" des Rechners klicken und "Wissenschaftlich" auswählen. Wenn Sie den Standardrechner wiederherstellen möchten, klicken Sie erneut auf "Ansicht" und wählen Sie "Standard".
 ` oder `^`-Taste Ihres Rechners für die Exponenten. Es ist fast unmöglich, größere Exponenten zu finden, wie z
` oder `^`-Taste Ihres Rechners für die Exponenten. Es ist fast unmöglich, größere Exponenten zu finden, wie z  von Hand, aber Taschenrechner können das problemlos handhaben. Der Button dafür ist meist deutlich genug gekennzeichnet. Der Windows-Rechner kann zu einem wissenschaftlichen Rechner erweitert werden, indem Sie auf die Registerkarte "Ansicht" des Rechners klicken und "Wissenschaftlich" auswählen. Wenn Sie den Standardrechner wiederherstellen möchten, klicken Sie erneut auf "Ansicht" und wählen Sie "Standard".
von Hand, aber Taschenrechner können das problemlos handhaben. Der Button dafür ist meist deutlich genug gekennzeichnet. Der Windows-Rechner kann zu einem wissenschaftlichen Rechner erweitert werden, indem Sie auf die Registerkarte "Ansicht" des Rechners klicken und "Wissenschaftlich" auswählen. Wenn Sie den Standardrechner wiederherstellen möchten, klicken Sie erneut auf "Ansicht" und wählen Sie "Standard".Methode 2 von 3: Exponenten addieren, subtrahieren und multiplizieren

1. Potenzzahlen können nur addiert oder subtrahiert werden, wenn sie die gleiche Basis und den gleichen Exponenten haben. Wenn Sie es mit identischen Basen und Exponenten zu tun haben, wie z  , dann kannst du die Addition der Terme zu einer Multiplikation vereinfachen. Vergiss das nicht
, dann kannst du die Addition der Terme zu einer Multiplikation vereinfachen. Vergiss das nicht  kann betrachtet werden als
kann betrachtet werden als  , so dass
, so dass  durch Hinzufügen, wobei `1 davon + 1 davon = 2 davon`, was auch immer `das` sein mag. Addiere einfach die Anzahl der gleichen Terme (die mit identischer Basis und Exponent) und multipliziere die Summe mit diesem Exponentialausdruck. Du kannst dann
durch Hinzufügen, wobei `1 davon + 1 davon = 2 davon`, was auch immer `das` sein mag. Addiere einfach die Anzahl der gleichen Terme (die mit identischer Basis und Exponent) und multipliziere die Summe mit diesem Exponentialausdruck. Du kannst dann  löse und multipliziere diese Antwort mit zwei. Denken Sie daran, dass dies möglich ist, weil eine Multiplikation nichts anderes ist, als eine Addition umzuschreiben, denn
löse und multipliziere diese Antwort mit zwei. Denken Sie daran, dass dies möglich ist, weil eine Multiplikation nichts anderes ist, als eine Addition umzuschreiben, denn  . Hier einige Beispiele:
. Hier einige Beispiele:
 , dann kannst du die Addition der Terme zu einer Multiplikation vereinfachen. Vergiss das nicht
, dann kannst du die Addition der Terme zu einer Multiplikation vereinfachen. Vergiss das nicht  kann betrachtet werden als
kann betrachtet werden als  , so dass
, so dass  durch Hinzufügen, wobei `1 davon + 1 davon = 2 davon`, was auch immer `das` sein mag. Addiere einfach die Anzahl der gleichen Terme (die mit identischer Basis und Exponent) und multipliziere die Summe mit diesem Exponentialausdruck. Du kannst dann
durch Hinzufügen, wobei `1 davon + 1 davon = 2 davon`, was auch immer `das` sein mag. Addiere einfach die Anzahl der gleichen Terme (die mit identischer Basis und Exponent) und multipliziere die Summe mit diesem Exponentialausdruck. Du kannst dann  löse und multipliziere diese Antwort mit zwei. Denken Sie daran, dass dies möglich ist, weil eine Multiplikation nichts anderes ist, als eine Addition umzuschreiben, denn
löse und multipliziere diese Antwort mit zwei. Denken Sie daran, dass dies möglich ist, weil eine Multiplikation nichts anderes ist, als eine Addition umzuschreiben, denn  . Hier einige Beispiele:
. Hier einige Beispiele: 
2. Multiplizieren Sie Zahlen mit derselben Basis, indem Sie die Exponenten zusammenzählen. Wenn Sie zwei Exponenten mit derselben Basis haben, wie z  , dann musst du nur noch die beiden Exponenten mit derselben Basis addieren. So,
, dann musst du nur noch die beiden Exponenten mit derselben Basis addieren. So, . Wenn Sie dies etwas seltsam finden, teilen Sie es in kleinere Teile auf, um zu verstehen, wie das System funktioniert:
. Wenn Sie dies etwas seltsam finden, teilen Sie es in kleinere Teile auf, um zu verstehen, wie das System funktioniert:
 , dann musst du nur noch die beiden Exponenten mit derselben Basis addieren. So,
, dann musst du nur noch die beiden Exponenten mit derselben Basis addieren. So, . Wenn Sie dies etwas seltsam finden, teilen Sie es in kleinere Teile auf, um zu verstehen, wie das System funktioniert:
. Wenn Sie dies etwas seltsam finden, teilen Sie es in kleinere Teile auf, um zu verstehen, wie das System funktioniert:






3. Multiplizieren Sie eine Exponentialzahl mit einer anderen Potenz, wie z ( x 2 ) 5  . Wenn Sie eine Zahl mit einer bestimmten Potenz erhöhen und das Ganze wird eine bestimmte Potenz, multiplizieren Sie einfach die beiden Exponenten. So,
. Wenn Sie eine Zahl mit einer bestimmten Potenz erhöhen und das Ganze wird eine bestimmte Potenz, multiplizieren Sie einfach die beiden Exponenten. So,  . Wenn Sie verwirrt sind, denken Sie noch einmal darüber nach, was diese Symbole eigentlich bedeuten.
. Wenn Sie verwirrt sind, denken Sie noch einmal darüber nach, was diese Symbole eigentlich bedeuten.  meint nur dich
meint nur dich  Multipliziert 5 mal mit sich selbst, also:
Multipliziert 5 mal mit sich selbst, also:
 . Wenn Sie eine Zahl mit einer bestimmten Potenz erhöhen und das Ganze wird eine bestimmte Potenz, multiplizieren Sie einfach die beiden Exponenten. So,
. Wenn Sie eine Zahl mit einer bestimmten Potenz erhöhen und das Ganze wird eine bestimmte Potenz, multiplizieren Sie einfach die beiden Exponenten. So,  . Wenn Sie verwirrt sind, denken Sie noch einmal darüber nach, was diese Symbole eigentlich bedeuten.
. Wenn Sie verwirrt sind, denken Sie noch einmal darüber nach, was diese Symbole eigentlich bedeuten.  meint nur dich
meint nur dich  Multipliziert 5 mal mit sich selbst, also:
Multipliziert 5 mal mit sich selbst, also:



4. Stellen Sie sich negative Exponenten als Brüche oder den Kehrwert der Zahl vor. Weiß nicht was eine Gegenseitigkeit ist, kein Problem. Wenn Sie es mit einem negativen Exponenten zu tun haben, wie z  , dann mache den Exponenten positiv und setze diesen als Nenner unter eins, was zu
, dann mache den Exponenten positiv und setze diesen als Nenner unter eins, was zu  . Hier ein paar zusätzliche Beispiele:
. Hier ein paar zusätzliche Beispiele:
 , dann mache den Exponenten positiv und setze diesen als Nenner unter eins, was zu
, dann mache den Exponenten positiv und setze diesen als Nenner unter eins, was zu  . Hier ein paar zusätzliche Beispiele:
. Hier ein paar zusätzliche Beispiele:


5. Dividiere zwei Zahlen mit gleicher Basis durch Subtraktion der Exponenten. Division ist das Gegenteil von Multiplikation, und obwohl sie nicht genau als Gegensätze gelöst werden, sind sie hier. Wenn Sie es mit der Gleichung zu tun haben  , subtrahiere einfach den oberen Exponenten vom unteren und belasse die Basis so wie sie ist. So,
, subtrahiere einfach den oberen Exponenten vom unteren und belasse die Basis so wie sie ist. So,  , oder 16.
, oder 16.
 , subtrahiere einfach den oberen Exponenten vom unteren und belasse die Basis so wie sie ist. So,
, subtrahiere einfach den oberen Exponenten vom unteren und belasse die Basis so wie sie ist. So,  , oder 16.
, oder 16. , umgeschrieben werden als
, umgeschrieben werden als  . Negative Exponenten bilden Brüche.
. Negative Exponenten bilden Brüche.
6. Probieren Sie einige Übungsübungen aus, um sich an den Umgang mit Potenzzahlen zu gewöhnen. Die folgenden Übungen üben alles bisher Besprochene. Wählen Sie für die Antwort einfach die Zeile aus, die das Problem enthält.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Denken Sie daran, dass eine Zahl ohne Potenz einen Exponenten von 1 . hat
Denken Sie daran, dass eine Zahl ohne Potenz einen Exponenten von 1 . hat =
= 
 =
= 
Methode 3 von 3: Brüche als Potenzzahlen lösen

1. Behandeln Sie Brüche in Form von Potenzzahlen, wie z x 1 2  als Quadratwurzel.
als Quadratwurzel.  ist in der Tat genau das gleiche wie
ist in der Tat genau das gleiche wie  . Dies gilt unabhängig vom Nenner des Bruchs, also
. Dies gilt unabhängig vom Nenner des Bruchs, also  wird die quadratische Wurzel von x, auch geschrieben als
wird die quadratische Wurzel von x, auch geschrieben als ![Exponenten lösen {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 als Quadratwurzel.
als Quadratwurzel.  ist in der Tat genau das gleiche wie
ist in der Tat genau das gleiche wie  . Dies gilt unabhängig vom Nenner des Bruchs, also
. Dies gilt unabhängig vom Nenner des Bruchs, also  wird die quadratische Wurzel von x, auch geschrieben als
wird die quadratische Wurzel von x, auch geschrieben als ![Exponenten lösen {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Wurzeln sind die Umkehrung der Exponenten. Zum Beispiel, wenn Sie die Antwort von
zur vierten Potenz, dann kommst du zurück zu
, und das kann auch
auch geschrieben werden als
. Ein weiteres Beispiel ist
und dann
und somit
.

2. Mache den Zähler zu einem normalen Exponenten für einen gemischten Bruch. mag unmöglich aussehen, ist aber einfach, wenn Sie sich daran erinnern, wie Exponenten multipliziert werden. Machen Sie die Basis zu einer Quadratwurzel, wie bei einem normalen Bruch, und potenzieren Sie das Ganze an der Spitze des Bruchs. Wenn es Ihnen schwerfällt, sich daran zu erinnern, gehen Sie die Theorie noch einmal durch. Das gilt letztendlich
mag unmöglich aussehen, ist aber einfach, wenn Sie sich daran erinnern, wie Exponenten multipliziert werden. Machen Sie die Basis zu einer Quadratwurzel, wie bei einem normalen Bruch, und potenzieren Sie das Ganze an der Spitze des Bruchs. Wenn es Ihnen schwerfällt, sich daran zu erinnern, gehen Sie die Theorie noch einmal durch. Das gilt letztendlich  einfach gleich
einfach gleich  Zum Beispiel:
Zum Beispiel:
 mag unmöglich aussehen, ist aber einfach, wenn Sie sich daran erinnern, wie Exponenten multipliziert werden. Machen Sie die Basis zu einer Quadratwurzel, wie bei einem normalen Bruch, und potenzieren Sie das Ganze an der Spitze des Bruchs. Wenn es Ihnen schwerfällt, sich daran zu erinnern, gehen Sie die Theorie noch einmal durch. Das gilt letztendlich
mag unmöglich aussehen, ist aber einfach, wenn Sie sich daran erinnern, wie Exponenten multipliziert werden. Machen Sie die Basis zu einer Quadratwurzel, wie bei einem normalen Bruch, und potenzieren Sie das Ganze an der Spitze des Bruchs. Wenn es Ihnen schwerfällt, sich daran zu erinnern, gehen Sie die Theorie noch einmal durch. Das gilt letztendlich  einfach gleich
einfach gleich  Zum Beispiel:
Zum Beispiel:

![Exponenten lösen x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Exponenten lösen ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Sie können Brüche in Form von Potenzzahlen addieren, subtrahieren und multiplizieren – ganz wie Sie es normalerweise tun würden. Es ist viel einfacher, die Exponenten zu addieren oder zu subtrahieren, bevor Sie sie lösen oder in Quadratwurzeln umwandeln. Wenn die Basis gleich und der Exponent gleich ist, können Sie sie einfach addieren und subtrahieren. Wenn nur die Basis gleich ist, können Sie die Exponenten wie gewohnt multiplizieren und dividieren, solange Sie berücksichtigen wie man Brüche addiert und subtrahiert. Zum Beispiel:


Tipps
- Die meisten Taschenrechner haben eine Taste für Exponenten – drücken Sie nach der Eingabe der Basis – um Probleme mit Potenzzahlen zu lösen.Normalerweise sieht das aus wie ein ^ oder x^y.
- `Vereinfachen` in der Mathematik bedeutet Nehmen Sie die erforderlichen Änderungen vor, um die einfachste Form der fraglichen Ausdrücke zu erhalten.
- 1 ist das Identitätselement von Exponenten. Das bedeutet, dass jede reelle Zahl, die mit 1 potenziert wird (erste Potenz), die Zahl selbst ist, zum Beispiel:
Außerdem ist 1 das Identitätselement der Multiplikation (1 als Multiplikator, wie
) und aus der Division (1 als Dividende, wie
.
- Die Basis null zu null (0) ist undefiniert (Englisch: dne, ist nicht vorhanden). Computer oder Taschenrechner geben dann einen `Fehler` zurück. Denken Sie daran, dass jede Zahl ungleich Null, die hoch 0 ist, immer gleich 1 . ist,
- Höhere Mathematik für imaginäre Zahlen ist beispielsweise,
, wodurch
; e ist eine irrationale, kontinuierliche Konstante von 2,71828..., und a ist eine beliebige Konstante. Der Beweis ist in den meisten höheren Mathematikbüchern zu finden.
Warnungen
- Ein exponentieller Anstieg lässt das Produkt immer schneller steigen, sodass die Antwort falsch erscheinen kann, wenn sie richtig ist. (Überprüfen Sie dies, indem Sie zum Beispiel eine Exponentialfunktion grafisch darstellen.: 2, wenn x einen Bereich verschiedener Werte hat).
Оцените, пожалуйста статью