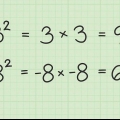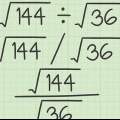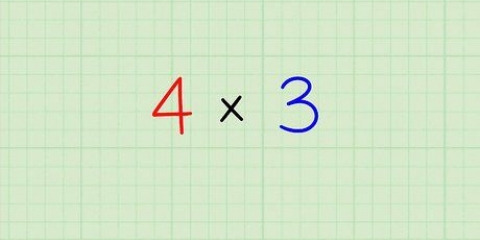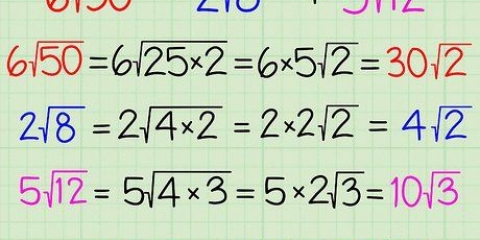Quadratwurzeln multiplizieren: 8 Schritte (mit Bildern)

Schritte
- Methode 1 von 2: Quadratwurzeln ohne Koeffizienten multiplizieren
- Methode 2 von 2: Quadratwurzeln mit Koeffizienten multiplizieren
Tipps
Notwendigkeiten

Genau wie beim Multiplizieren von ganzen Zahlen können Sie auch Quadratwurzeln (eine Quadratwurzelgleichung) miteinander multiplizieren. Manchmal haben Quadratwurzeln Koeffizienten (eine ganze Zahl vor dem Radikal), aber dies fügt der Multiplikation nur einen Schritt hinzu und ändert nichts am Prozess. Der schwierigste Teil der Quadratwurzelmultiplikation besteht darin, den Ausdruck zu vereinfachen, um die endgültige Antwort zu erhalten, aber selbst dieser Schritt ist einfach, wenn Sie Ihre perfekten Quadrate kennen.

Schritte

Methode 1 von 2: Quadratwurzeln ohne Koeffizienten multiplizieren

1. Multiplizieren Sie die Wurzeln zusammen. Ein Radicand (englisch) ist eine Zahl unter dem Radikal. Multiplizieren Sie Wurzeln wie ganze Zahlen. Stellen Sie sicher, dass das Produkt unter dem Radikalzeichen bleibt.

Wenn Sie beispielsweise berechnen $\sqrt{fünfzehn} \times \sqrt{5}$ ${sqrt{15}}times {sqrt{5}}$ , dann bekommst du $fünfzehn \times 5 = 75$ $15mal 5=75$ . Also, $\sqrt{fünfzehn} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}times {sqrt{5}}={sqrt{75}}$ .

2. Leite alle perfekten Quadrate aus der Quadratwurzel ab. Sie tun dies, indem Sie prüfen, ob ein perfektes Quadrat ein Faktor der Zahl unter dem Radikal ist. Wenn Sie kein perfektes Quadrat ableiten können, wurde Ihre Antwort bereits vereinfacht und Sie müssen nichts weiter tun.

Ein perfektes Quadrat ist das Ergebnis der Multiplikation einer Zahl (positive oder negative ganze Zahl) mit sich selbst. Zum Beispiel: 25 ist ein perfektes Quadrat, weil

5 \times 5 = 25

$5mal 5=25$ .

Zum Beispiel,

\sqrt{75}

${sqrt{75}}$ kann in das perfekte Quadrat 25 eingerechnet werden:

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25times 3}}$

3. Platziere die Quadratwurzel vor dem Radikal. Lassen Sie den anderen Faktor unter dem Radikal. Jetzt haben Sie den vereinfachten Ausdruck.

Zum Beispiel,

\sqrt{75}

${sqrt{75}}$ kann aufgelöst werden in

\sqrt{25 \times 3}

${sqrt{25times 3}}$ , für die Quadratwurzel von 25 (das ist 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25times 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

4. Berechnen Sie das Quadrat einer Quadratwurzel. In einigen Fällen müssen Sie eine Quadratwurzel mit sich selbst multiplizieren. Das Quadrieren einer Zahl und das Ziehen der Quadratwurzel einer Zahl sind entgegengesetzte Operationen; also machen sie sich gegenseitig rückgängig. Das Ergebnis des Quadrats einer Quadratwurzel ist einfach die Zahl unter dem Radikal.

Zum Beispiel,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}}times {sqrt{25}}=25$ . Sie erhalten dieses Ergebnis, weil

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}}times {sqrt{25}}=5times 5=25$ .

Methode 2 von 2: Quadratwurzeln mit Koeffizienten multiplizieren

1. Multiplizieren Sie die Koeffizienten. Ein Koeffizient ist eine Zahl für das Radikal. Ignoriere einfach den Rest und die Zahl darunter und multipliziere die beiden ganzen Zahlen miteinander. Platzieren Sie ihr Produkt vor dem ersten Radikal.

Achten Sie beim Multiplizieren von Koeffizienten auf Plus- und Minuszeichen. Denken Sie daran, dass eine negative Zahl mal eine positive Zahl ein negatives Ergebnis ergibt und eine negative Zahl mal eine negative Zahl ein positives Ergebnis ergibt.
Zum Beispiel bei der Berechnung $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}}times 2{sqrt{6}}$ , erst berechnen $3 \times 2 = 6$ $3mal 2=6$ . Die Aufgabe lautet nun wie folgt: $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}times {sqrt{6}}$ .

2. Multiplizieren Sie die Zahlen unter den Radikalen. Multiplizieren Sie dazu die Zahlen, als wären sie ganze Zahlen. Stellen Sie sicher, dass das Produkt unter dem Radikalzeichen bleibt.

Zum Beispiel für eine Aussage wie

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}times {sqrt{6}}$ , berechne das Produkt der Zahlen unter den Radikalen mit

2 \times 6 = 12

$2mal 6=12$ , so dass

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}}times {sqrt{6}}={sqrt{12}}$ . Die Aufgabe sieht nun so aus:

6 \sqrt{12}

$6{sqrt{12}}$ .

3. Ziehe, wenn möglich, alle Quadrate unter dem Wurzelzeichen heraus. Sie müssen dies tun, um Ihre Antwort zu vereinfachen. Wenn Sie ein Quadrat nicht lösen können, wurde Ihre Antwort bereits vereinfacht und Sie können diesen Schritt überspringen.

Ein Quadrat ist das Ergebnis der Multiplikation einer ganzen Zahl (positiv oder negativ) mit sich selbst. Zum Beispiel: 4 ist ein Quadrat, weil

2 \times 2 = 4

$2mal 2=4$ .

Zum Beispiel:

\sqrt{12}

${sqrt{12}}$ kann so faktorisiert werden, dass das Quadrat von 4 vor dem Radikal steht:

\sqrt{12}

${sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4times 3}}$

4. Multiplizieren Sie die Wurzel des Quadrats mit dem Koeffizienten. Lassen Sie den anderen Faktor unter dem Radikal. Dies ergibt einen vereinfachten Ausdruck.

Zum Beispiel,

6 \sqrt{12}

$6{sqrt{12}}$ kann aufgelöst werden in

6 \sqrt{4 \times 3}

$6{sqrt{4times 3}}$ , Danach können Sie die Quadratwurzel von 4 (also 2) ziehen und diese dann mit 6 multiplizieren:

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4times 3}}$
=

6 \times 2 \sqrt{3}

$6mal 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Tipps

Kenne deine Quadrate, denn das macht diesen Prozess viel einfacher!
Befolgen Sie die üblichen Regeln für das Vorzeichen einer Zahl, um zu bestimmen, ob der neue Koeffizient positiv oder negativ ist. Ein positiver Koeffizient multipliziert mit einem negativen Koeffizienten ergibt eine negative Zahl. Zwei positive Koeffizienten miteinander multipliziert oder zwei negative Koeffizienten miteinander multipliziert ergeben eine positive Zahl.
Alle Terme unter dem Radikal sind immer positiv, sodass Sie sich beim Multiplizieren von Zahlen unter einem Radikal keine Gedanken über das Vorzeichen machen müssen.