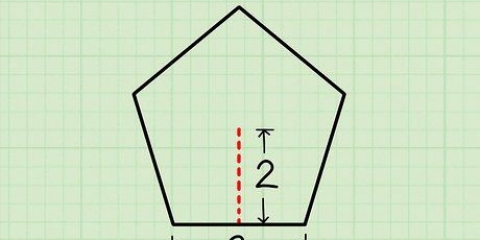
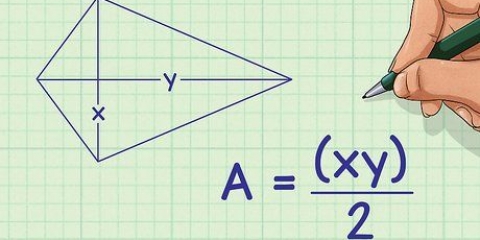Die Winkel in einem Dreieck (einem 3-seitigen Polygon) betragen 180 Grad. Die Winkel in einem Viereck (einem 4-seitigen Polygon) betragen 360 Grad. Die Winkel in einem Fünfeck (einem 5-seitigen Polygon) betragen 540 Grad. Die Winkel in einem Sechseck (einem 6-seitigen Polygon) betragen insgesamt 720 Grad. Die Winkel in einem Achteck (einem 8-seitigen Polygon) betragen insgesamt 1080 Grad. 
Wenn das Polygon ein regelmäßiges Polygon ist, teilen Sie einfach die Summe aller Winkel durch die Anzahl der Winkel. Somit ist jeder Winkel in einem gleichseitigen Dreieck 180/3=60 Grad, und jeder Winkel eines Quadrats ist 360/4=90 Grad. (Obwohl ein Rechteck per Definition kein regelmäßiges Vieleck ist, sind alle Winkel auch rechte Winkel, also 90 Grad). Wenn ein Polygon kein regelmäßiges Polygon ist, müssen Sie die Größe der anderen Winkel kennen, um die Größe des unbekannten Winkels zu berechnen. gehe zum nächsten schritt. 
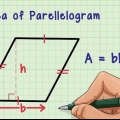
Wenn zwei der Winkel eines Dreiecks 60 und 80 Grad betragen, addieren Sie diese Winkel (60 + 80=140). Dann subtrahiere diese Summe von der Summe der Winkel eines Dreiecks, 180 Grad: 180-140=40 Grad. (Ein solches Dreieck, bei dem alle Winkel unterschiedlich sind, wird als skalenförmiges Dreieck bezeichnet). Sie können die obige Methode als Formel ausschreiben: ein=180 – (B + C), wobei ein der Winkel ist, den Sie bestimmen möchten, und B und C die Winkel, die bekannt sind. Ersetzen Sie bei Polygonen mit mehr als 3 Seiten `180` durch die Summe der Winkel, die für dieses Polygon spezifisch sind, und fügen Sie für jeden weiteren bekannten Winkel einen anderen Begriff hinzu. Für einige Polygone ist eine `schnellere Lösung` zur Bestimmung des unbekannten Winkels möglich. Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten und zwei gleich großen Winkeln. Ein Parallelogramm ist ein Viereck mit gegenüberliegenden Seiten gleicher Länge und diagonal gegenüberliegenden Winkeln gleicher Größe. 

Wenn Sie die Länge der gegenüberliegenden Seite (relativ zum Winkel) und die Länge der Hypotenuse (die dem rechten Winkel gegenüberliegende Seite) kennen, verwenden Sie die Sinusfunktion (die Länge der gegenüberliegenden Seite geteilt durch die Länge der Hypotenuse). die Seide). Wenn Sie die Länge der angrenzenden rechteckigen Seite und die Länge der Hypotenuse kennen, können Sie die Kosinusfunktion verwenden (die Länge der angrenzenden Seite geteilt durch die Länge der Hypotenuse). Wenn Sie die Längen der gegenüberliegenden Seiten und der angrenzenden Seiten kennen, können Sie die Tangentenfunktion verwenden (die Länge der gegenüberliegenden Seite geteilt durch die Länge der angrenzenden Seite). 
Dividiert man den umgekehrten Wert 5 durch die Hypotenuse (die Hypotenuse) 10, erhält man den Bruch 5 / 10=0.5. 
In den Tagen vor Taschenrechnern sollten Sie eine gedruckte Wertetabelle für Sinus, Cosinus und Tangens von Winkeln von 0 bis 90 Grad konsultieren. Folgen Sie der Sinusspalte, bis Sie den Wert `0.5` finden, und finden Sie dann den Winkel, der diesem Sinuswert entspricht. Wenn Sie einen Taschenrechner mit trigonometrischen Funktionen haben, können Sie den Sinus als Wert eingeben (wenn Sie den Taschenrechner noch nicht verwendet haben, um die gegenüberliegende Seite durch die Hypotenuse zu dividieren, um diesen Wert zu finden) und dann die entsprechende Taste oder die entsprechenden Tasten drücken. Drücken Sie je nach Taschenrechnermarke eine einzelne Taste mit der Bezeichnung `sin` oder eine Taste mit der Bezeichnung `Inv`, `2ndF` oder `Shift`, bevor Sie die `sin`-Taste drücken. Unabhängig von der Methode, mit der Sie dieses Beispiel lösen, sollten Sie in allen Fällen einen Winkel von 30 Grad finden.
Winkel berechnen
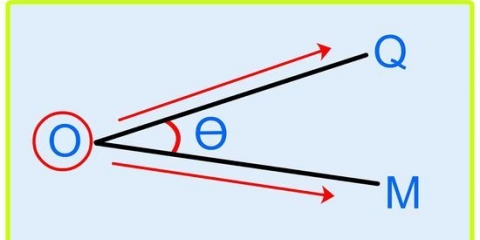
In der Geometrie ist ein Winkel der Abstand zwischen zwei Strahlen oder Liniensegmenten, die denselben Endpunkt oder Scheitelpunkt haben. Die gebräuchlichste Methode zum Messen von Winkeln ist in Grad, wobei ein Vollkreis 360 Grad beträgt. Sie können den Winkel in einem Polygon berechnen, wenn Sie die Form des Polygons und die Größe der anderen Winkel kennen, oder im Fall eines rechtwinkligen Dreiecks, wenn Sie die Größe der beiden Seiten kennen.
Schritte
Methode 1 von 2: Berechnung des Winkels in einem Polygon

1. Zählen Sie die Anzahl der Seiten des Polygons.

2. Finde die Summe aller Winkel im Polygon. Die Formel zum Ermitteln des Gesamtmaßes aller Innenwinkel in einem Polygon lautet (n – 2) x 180, wobei n ist die Anzahl der Seiten sowie die Anzahl der Winkel des Polygons. Einige gebräuchliche Summen der Winkel in einem Polygon sind:

3. Bestimmen Sie, ob das Polygon ein regelmäßiges Polygon ist. Ein regelmäßiges Vieleck ist ein Vieleck mit allen Seiten gleich lang und allen Winkeln gleich groß. Gleichseitige Dreiecke und Quadrate sind Beispiele für regelmäßige Vielecke, während das Pentagon in Washington DC ein Beispiel für ein regelmäßiges Fünfeck ist und ein Stoppschild ein Beispiel für ein regelmäßiges Achteck ist.

4. Addiere die bekannten Winkel des Polygons und subtrahiere die Summe von der Summe aller Winkelmaße des Polygons. Die meisten ähnlichen Geometrieprobleme funktionieren mit Dreiecken oder Vierecken, weil weniger Zahlen zu verarbeiten sind, und deshalb werden wir.
Methode 2 von 2: Berechnen Sie den Winkel in einem rechtwinkligen Dreieck

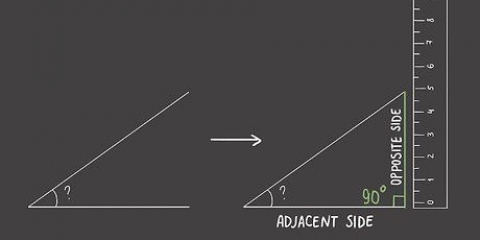
1. Finden Sie heraus, was Sie bereits wissen. Ein rechtwinkliges Dreieck wird so genannt, weil einer seiner Winkel ein rechter Winkel ist. Sie können die anderen Winkel bestimmen, wenn Sie einen der folgenden Punkte kennen:
- Die Größe des dritten Winkels. In diesem Fall können Sie die Größe des Winkels zu 90, der Gradzahl des rechten Winkels, addieren und dann die Summe von 180 . subtrahieren.
- Die Größe von zwei Seiten des Dreiecks. In diesem Fall können Sie die Größe des Winkels mithilfe der Trigonometrie bestimmen.

2. Bestimmen Sie, welche trigonometrische Funktion verwendet werden soll. Trigonometrische Funktionen sind Verhältnisse zwischen zwei der drei Seiten eines Dreiecks. Obwohl es sechs trigonometrische Funktionen gibt, werden die folgenden drei am häufigsten verwendet:

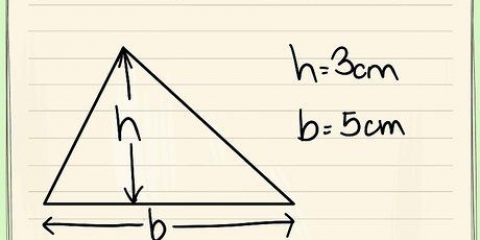
3. Finden Sie das Verhältnis der beiden bekannten Seiten. Nehmen Sie für dieses Beispiel an, dass die dem Winkel gegenüberliegende Seite eine Länge von 5 und die Hypotenuse eine Länge von 10 . hat. Da damit das Gegenteil und die Hypotenuse gegeben sind, handelt es sich hier um das Verhältnis des Sinus.

4. Finden Sie den Winkel entsprechend dem Verhältnis der trigonometrischen Funktion. Da wir den Sinus verwenden, um den Winkel zu finden, wird der gesuchte Winkel Arkussinus oder inverser Sinus genannt. Es gibt zwei Möglichkeiten, es zu finden:
Tipps
- Winkel werden durch die Gradzahl bezeichnet, die sie messen. Wie oben erwähnt, hat ein rechter Winkel 90 Grad. Ein Winkel größer als 0, aber kleiner als 90 Grad ist ein spitzer Winkel. Ein Winkel von mehr als 90, aber weniger als 180 Grad ist ein stumpfer Winkel. Ein Winkel von 180 Grad ist ein gerader Winkel, während ein Winkel von mehr als 180 Grad ein Wiedereintrittswinkel ist.
- Zwei Winkel mit insgesamt 90 Grad werden als Komplementärwinkel bezeichnet (Die beiden anderen Winkel als der rechte Winkel in einem rechtwinkligen Dreieck sind Komplementärwinkel). Zwei Winkel, deren Winkel zusammen 180 Grad ergeben, werden Ergänzungswinkel genannt.
Notwendigkeiten
- Trigonometrische Tabellen oder ein Taschenrechner mit trigonometrischen Funktionen
Оцените, пожалуйста статью