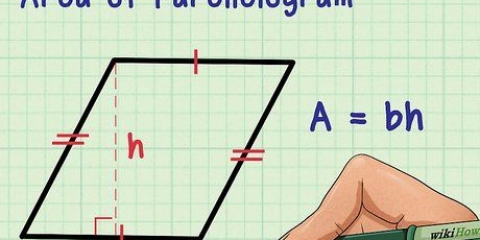Da alle vier Seiten eines Quadrats gleich sind, ist die "Länge" des Quadrats identisch mit seiner "Breite". In diesem Fall müssen Sie nur in eine Richtung messen. 
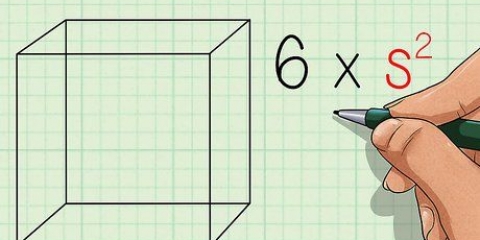
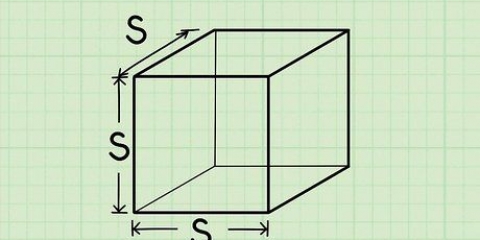
Angenommen, Sie haben einen rechteckigen Bereich mit einer Länge von 4 Zentimetern und einer Breite von 3 Zentimetern. In diesem Fall beträgt die Fläche des Rechtecks 4 × 3 =12 Quadratzentimeter. Da bei Quadraten alle vier Seiten gleich sind, können Sie einfach eine Seite messen und mit sich selbst multiplizieren (auch "Quadrieren" oder Potenzieren in die zweite Potenz genannt), um die Fläche in Quadratzentimetern zu berechnen. 

Wenn Sie also eine Basis mit einer Länge von 4 Zentimetern haben und die entsprechende Höhe 3 Zentimeter beträgt, dann ist Ihr Ergebnis 2 x 3 = 6 Quadratzentimeter. 
Wenn also die Länge einer Seite 5 Zentimeter und die Höhe 4 Zentimeter beträgt, dann ist die resultierende Fläche 5 x 4 = 20 Zentimeter. 
Wenn also die lange Seite Ihres Trapezes 6 Zentimeter beträgt, die kurze Seite 4 Zentimeter und die Höhe 5 Zentimeter beträgt, ist das Ergebnis ½ x 5 x (6 + 4) = 25 cm. 
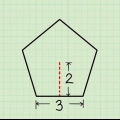
Wenn Sie also ein Sechseck mit 6 gleichen Seiten von jeweils 4 Zentimetern (also P=6 x 4=24) und ein Apothem von 3,5 Zentimetern haben, dann lautet die Rechnung ½ x 24 x 3,5=42 cm. 
Wenn Sie also ein regelmäßiges Achteck mit einer Länge von 4 Zentimetern haben, berechnen Sie (2 x 16) x (1 + 1,4) = 32 x 2,4 = 76,8 cm. 

Zum Beispiel 400 Quadratfuß = 400 x 144 = 57600 Zoll. 
Ebenso entspricht 1 Quadratmeter 10.000 Quadratzentimeter, und dieser ein Quadratkilometer entspricht 10.000.000.000 Quadratzentimeter. Also, ein Quadratkilometer = 10.000.000.000 Quadratzentimeter x 0,155 = 1.550.003.100 Zoll.
Quadratzentimeter berechnen
Die Bestimmung des Quadratzentimeters (auch als cm geschrieben) in einem zweidimensionalen Raum ist normalerweise recht einfach. In den einfachsten Fällen, wie einem Quadrat oder Rechteck, lässt sich die Fläche in Quadratzentimetern mit der Gleichung berechnen Länge × Breite. Der Bereich anderer Formen (Kreise, Dreiecke usw.).) kann über eine Reihe spezialisierter mathematischer Gleichungen berechnet werden. Außerdem können Sie bei Bedarf problemlos von Quadratfuß oder Quadratzentimeter in Quadratzoll umrechnen.
Schritte
Methode 1 von 3: Quadratzentimeter in einem Quadrat oder Rechteck bestimmen

1. Besondere Länge der zu messenden Fläche. Quadrate und Rechtecke haben vier gerade Seiten. Bei Rechtecken sind die gegenüberliegenden Seiten gleich lang, bei Quadraten sind alle vier Seiten gleich. Messen Sie eine der Seiten des Quadrats oder die längste Seite des Rechtecks für die Länge.

2. Besondere Breite der zu messenden Fläche. Dann misst du eine der Seiten, die an die gerade gemessene Seite angrenzt. Diese Seite sollte die erste Seite in einem 90-Grad-Winkel schneiden. Dieses zweite Maß ist die Breite des Quadrats oder Rechtecks.

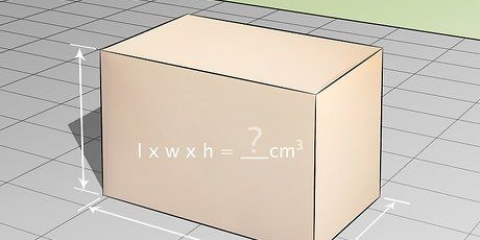
3. Länge × Breite multiplizieren. Multiplizieren Sie die Länge und Breite Ihres Quadrats oder Rechtecks, um die Fläche in Quadratzentimetern zu ermitteln.
Methode 2 von 3: Bestimmen der Fläche für andere Formen

1. Finden Sie die Fläche eines Kreises mit der Gleichung area=pi × r. Um die Fläche eines Kreises in Quadratzentimetern zu berechnen, müssen Sie nur den Abstand vom Mittelpunkt des Kreises zum Rand in Zentimetern kennen. Dieser Abstand wird als bezeichnet Strahl des Kreises. Sobald Sie diesen Wert kennen, ersetzen Sie ihn durch `r` in der obigen Gleichung. Multiplizieren Sie den Radius mit sich selbst, dann mit der mathematischen Konstante Pi (3.1415926...) um die Anzahl der Quadratzentimeter innerhalb des Kreises zu bestimmen.
- Ein Kreis mit einem Radius von 4 Zentimetern hat also eine Fläche von 50,27 Quadratzentimetern, das Produkt von 3,14 x 16.

2. Bestimmen Sie die Fläche eines Dreiecks mit der Gleichung Fläche=1/2 b × h in Quadratzentimetern. Die Fläche eines Dreiecks erhält man, indem man die Basis (`b`) mit der Höhe (`h`) multipliziert. Die Basis eines Dreiecks ist die Länge einer seiner Seiten, während seine Höhe der Abstand von der "Basis" zur gegenüberliegenden Ecke ist, gemessen in einem Winkel von 90 Grad von der "Basis". Die Fläche eines Dreiecks kann anhand seiner Basis und Höhe für jede seiner drei Seiten und den gegenüberliegenden Winkel berechnet werden.

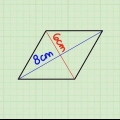
3. Finden Sie die Fläche eines Parallelogramms mit der Gleichung Area=b × h. Parallelogramme ähneln Rechtecken; der einzige Unterschied besteht darin, dass ihre Winkel nicht unbedingt 90 Grad betragen. Die Berechnung der Fläche eines Parallelogramms in Quadratzentimetern ähnelt der eines Rechtecks - multiplizieren Sie einfach die Basis eines Parallelogramms mit seiner Höhe und stellen Sie sicher, dass beide Maße in Zentimetern angegeben sind. Die Basis ist die Länge einer der Seiten, während die Höhe der im rechten Winkel gemessene Abstand von der Basis zur gegenüberliegenden Seite ist.

4. Finden Sie die Fläche eines Trapezes mit der Gleichung Fläche = 1/2 × h × (B + b). Ein Trapez ist ein Viereck mit zwei parallelen Seiten und zwei nicht parallelen Seiten. Um die Fläche in Quadratzentimetern zu berechnen, müssen Sie drei Maße (in Zentimetern) kennen: die Länge der längsten parallelen Seite (`B`), die Länge der kürzeren parallelen Seite (`b`) und die Höhe ( ` h`) des Trapezes (der Abstand zwischen den beiden parallelen Seiten, im rechten Winkel gemessen). Addiere die Längen der beiden Seiten zusammen, multipliziere das mit der Höhe und halbiere dann das Ergebnis, um die Fläche des Trapezes zu ermitteln.

5. Finden Sie die Fläche eines Sechsecks mit der Gleichung Fläche=½ × P × a. Diese Formel funktioniert für jedes regelmäßige Sechseck, d. h. es hat 6 gleiche Seiten und 6 gleiche Winkel. P stellt den Umfang oder die 6-fache Länge einer Seite (6 x s) für ein regelmäßiges Sechseck dar. ein stellt das Apothem dar – die Länge von der Mitte des Sechsecks bis zur Mitte einer Seite (d. h. auf halbem Weg zwischen zwei beliebigen Ecken). Multiplizieren Sie dies und halbieren Sie das Ergebnis, um die Fläche zu finden.

6. Finden Sie die Fläche eines Achtecks mit der Gleichung area=2a² × (1 + √2). Für ein regelmäßiges Achteck (mit 8 gleichen Seiten und 8 gleichen Winkeln) müssen Sie nur die Länge einer Seite (`a` in der Formel) kennen, um die Fläche zu berechnen. Verwenden Sie diese Messung in der Formel und Sie haben Ihr Ergebnis.
Methode 3 von 3: Umrechnung in Quadratzoll

1. Konvertieren Sie die Abmessungen in Zoll, bevor Sie Berechnungen durchführen. Um Ihre endgültige Antwort in Quadratzoll zu erhalten, ist es am besten, alle für die Formel erforderlichen Maße (wie Länge, Höhe oder Apothem) in Zoll anzugeben. Wenn also die Seiten Ihres Quadrats jeweils 1 Fuß betragen, konvertieren Sie dies in 12 Zoll, bevor Sie die Fläche berechnen. Hier sind die Umrechnungsfaktoren für häufig verwendete Maßeinheiten:
- 1 Fuß = 12 Zoll
- 1 Yard = 36 Zoll
- 1 Zentimeter = 0,3937 Zoll
- 1 Meter = 39,3701 Zoll
- 1 Millimeter = 0,0394 Zoll

2. Mit 144 multiplizieren, um von Quadratfuß in Quadratzoll umzurechnen. 1 Quadratfuß ist buchstäblich 1 Quadratfuß (oder 1 Fuß mal 1 Fuß); Dies ist das gleiche wie 12 Zoll mal 12 Zoll oder 144 Quadratzoll. Wenn Sie also eine Fläche in Quadratfuß haben, multiplizieren Sie sie mit 144, um die Fläche in Quadratzoll zu erhalten.

3. Mit 0,155 multiplizieren, um Quadratzentimeter in Quadratzoll umzurechnen. 1 Zentimeter entspricht ungefähr 0,394 Zoll und 0,394 zum Quadrat (0,394 x 0,394) i entspricht 0,155. Wenn Sie also eine Fläche von 250 cm in Zoll umrechnen müssen, multiplizieren Sie 250 mit 0,155 und Sie erhalten 38,75 Zoll.
"Quadratzentimeter berechnen"
Оцените, пожалуйста статью