Um s³ zu finden, multipliziere s dreimal mit sich selbst: s³ = s x s x s 
Wenn Sie nicht 100% sicher sind, ob Ihre Form ein Würfel ist, messen Sie alle Seiten, um zu sehen, ob sie gleich sind. Ist dies nicht der Fall, müssen Sie das Volumen eines Strahls mit der folgenden Methode berechnen. Hinweis: In den Beispielbildern sind die Maße in Zoll (in) angegeben, wir verwenden jedoch Zentimeter (cm). 




Beispiel: Die Länge dieses Balkens beträgt 4 cm, also l = 4 cm. Machen Sie sich keine Sorgen darüber, welche Seite die Länge hat usw. Solange Sie nur drei verschiedene Seiten messen, ist das Ergebnis das gleiche. 
Beispiel: Die Breite dieses Balkens beträgt 3 cm, also b = 3 cm. Wenn Sie den Balken mit einem Lineal oder Maßband messen, vergessen Sie nicht, alles in derselben Maßeinheit aufzuschreiben. 
Beispiel: Die Höhe dieses Balkens beträgt 6 cm, also h = 6 cm. 
In diesem Beispiel ist l = 4, b = 3 und h = 6. Das Ergebnis ist daher V = 4 x 3 x 6 = 72. 
Wenn die Abmessungen des Balkens beispielsweise in Metern angegeben sind, erhalten Sie l = 2 m, b = 4 m und h = 8 m. Das Volumen wäre dann 2 m x 4 m x 8 m = 64 m³. 

In den meisten Fällen reicht es aus, Pi auf 3,14 . zu runden. Frage deinen Lehrer, was er/sie will. Die Formel zum Ermitteln des Volumens eines Zylinders ist tatsächlich der des Volumens eines Balkens sehr ähnlich: Sie multiplizieren die Höhe der Form mit der Grundfläche. Bei einem Balken beträgt die Grundfläche l x b, bei einem Zylinder ist es π x r², die Fläche eines Kreises mit Radius r. 

Eine andere Möglichkeit besteht darin, den Umfang des Kreises (den Abstand um ihn herum) mit einer Schnur oder einem Maßband zu messen. Dann setze das Ergebnis in diese Formel ein: C (Umfang) ist 2 x π x r. Teilen Sie den Umfang durch 2 x π (6.28) und Sie haben den Radius. Wenn der gemessene Umfang beispielsweise 8 cm beträgt, beträgt der Radius 1,27 cm. Wenn Sie wirklich eine genaue Messung benötigen, können Sie mit beiden Methoden überprüfen, ob die Ergebnisse gleich sind. Wenn nicht, überprüfen Sie es erneut. Die Umfangsmethode liefert normalerweise ein genaueres Ergebnis. 
Wenn der Radius 4 cm beträgt, ist die Fläche des Kreises A = π x 4². 4² = 4 x 4 oder 16. 16 xπ = 16 x 3,14 = 50,24 cm². Wenn statt des Radius der Durchmesser der Basis bekannt ist, denken Sie daran, dass d = 2 x r. Dann musst du den Durchmesser durch zwei teilen, um den Radius zu finden. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


Die Formel für gerade Pyramiden, bei denen die Spitze direkt über der Mitte der Basis liegt, ist die gleiche wie bei schrägen Pyramiden, bei denen die Spitze nicht in der Mitte liegt. 
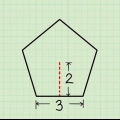
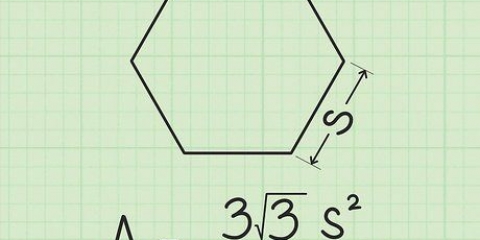
Die Formel für die Fläche eines Dreiecks lautet A = 1/2 x b x h, wobei b die Basis und h die Höhe ist. Es ist möglich, die Fläche jedes regelmäßigen Vielecks mit der Formel A = 1/2 xpxa zu berechnen, wobei A die Fläche ist, p der Umfang ist und a das Apothem ist, das der Abstand vom Mittelpunkt der Form zu . ist die Mitte einer der Seiten. Sie können es sich auch einfach machen und einen Online-Rechner für regelmäßige Polygone verwenden. 

Hätten wir eine andere Pyramide mit einer Grundfläche mit einer Fläche von 26 und einer Höhe von 8 gehabt, wäre das Ergebnis gewesen: 1/3 x 26 x 8 = 69,33. 


Der Teil π x r² bezieht sich auf die Fläche des Kreises, die die Basis des Kegels bildet. Die Formel für das Volumen des Kegels ist also 1/3 x b x h, genau wie die Formel für die Pyramide in der obigen Methode! 
In diesem Beispiel beträgt der Radius 3 cm. Setzen wir das in die Formel ein, erhalten wir: A = π x 3². 3² = 3 x3 oder 9, also A = π x 9. A = 28,27 cm². 


In unserem Beispiel ist das 141,35 x 1/3 = 47,12, das Volumen des Kegels. Nochmal: 1/3 x π x 3² x 5 = 47,12. 




Wenn Sie beispielsweise die Kugel messen und sehen, dass der Umfang 18 cm beträgt, teilen Sie dies durch 6,28, Sie wissen, dass der Radius 2,87 cm beträgt. Es kann schwierig sein, eine Kugel zu messen, daher ist es am besten, sie dreimal zu messen und sie zu mitteln (addiere die drei Messungen zusammen und dividiere durch drei), um die Messung so genau wie möglich zu erhalten. Wenn Sie beispielsweise dreimal gemessen haben und die Ergebnisse 18 cm, 17,75 cm und 18,2 cm waren, addieren Sie dies zusammen (18 + 17,5 + 18,2 = 53,95) und dividieren Sie durch 3 (53,95/3 = 17,98). Sie verwenden diesen Durchschnitt bei der Berechnung des Volumens. 


In unserem Beispiel wird es also 36 x 3,14 = 113,09. 
Volumen berechnen
- Schritte
- Methode 1 von 6: Das Volumen eines Würfels berechnen
- Methode 2 von 6:Berechnung des Strahlvolumens.
- Methode 3 von 6: Berechnung des Volumens eines Zylinders
- Methode 4 von 6: Berechnung des Volumens einer regelmäßigen Pyramide
- Methode 5 von 6: Berechnung des Volumens eines Kegels
- Methode 6 von 6: Berechnung des Volumens einer Kugel
Das Volumen einer Figur ist der dreidimensionale Raum, den die Figur einnimmt. Sie können das Volumen als die Menge an Wasser (oder Luft, Sand usw.).) das würde in die Form passen, wenn sie komplett gefüllt wäre. Gebräuchliche Maßeinheiten für Volumen sind Kubikzentimeter und Kubikmeter.In diesem Artikel erfahren Sie, wie Sie das Volumen von sechs verschiedenen dreidimensionalen Formen berechnen, die häufig bei mathematischen Tests vorkommen, einschließlich des Würfels, der Kugel und des Kegels. Sie werden sehen, dass es viele Ähnlichkeiten gibt, die es Ihnen leicht machen, sich daran zu erinnern. Sehen Sie, ob Sie diese Übereinstimmungen finden können!
Schritte
Methode 1 von 6: Das Volumen eines Würfels berechnen

1. Erkenne einen Würfel. Ein Würfel ist eine dreidimensionale Form mit sechs identischen quadratischen Flächen.Mit anderen Worten, es ist überall eine Kiste mit gleichen Seiten.
- Ein Würfel ist ein gutes Beispiel für einen Würfel, den Sie vielleicht zu Hause haben. Würfelzucker oder Kinderklötze sind oft auch Würfel.

2. Lerne die Formel um das Volumen des Würfels zu berechnen. Da alle Seitenlängen des Würfels gleich lang sind, ist die Formel zur Berechnung des Würfelvolumens sehr einfach. Die Stelle, an der sich zwei Seiten treffen, wird Rippe genannt. Wir kürzen Lautstärke auf "V". Die Rippen oder die Seitenlänge nennen wir hier "S". Die Formel lautet dann V = s³

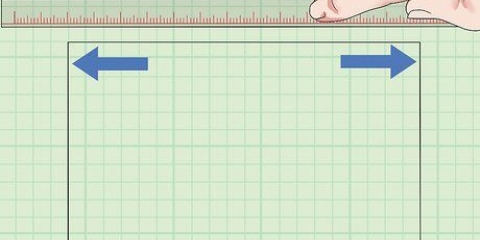
3. Finden Sie die Länge einer Seite des Würfels. Je nach Auftrag kann diese Information schon vorhanden sein, aber eventuell musst du sie auch selbst mit einem Lineal nachmessen. Denken Sie daran, da es sich um einen Würfel handelt, sollten alle Seitenlängen gleich sein, also spielt es keine Rolle, welche Sie messen.

4. Setze die Seitenlänge in die Formel V = s³ ein und berechne sie. Wenn Sie beispielsweise gemessen haben, dass die Seitenlänge Ihres Würfels 5 cm beträgt, würden Sie die Formel wie folgt schreiben: V = (5)³. 5 x 5 x 5 = 125 cm³, also das Volumen deines Würfels!

5. Achte darauf, dass du deine Antwort in Kubikzentimetern schreibst. Im obigen Beispiel wurde der Würfel in Zentimetern gemessen, die Antwort muss also in Kubikzentimetern angegeben werden. Wäre die Seitenlänge des Würfels 3 Meter gewesen, hätte das Volumen V = (3 m)³ = 27 m³ . betragen.
Methode 2 von 6:Berechnung des Strahlvolumens.

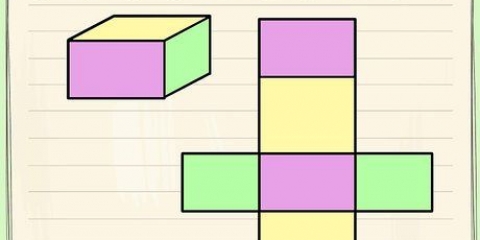
1. Erkenne einen Strahl. Ein Balken ist eine Figur, die aus sechs rechteckigen Flächen besteht. Es ist also eigentlich ein dreidimensionales Rechteck, eine Art Kiste.
- Eigentlich ist ein Würfel nur ein spezieller Balken, bei dem alle Seiten gleich sind.

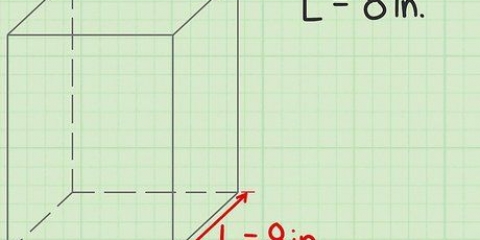
2. Lernen Sie die Formel zur Berechnung des Volumens eines Balkens. Die Formel für das Volumen eines Balkens lautet V = Länge (l) x Breite (b) x Höhe (h) oder V = l x b x h. Hinweis: Die Bilder zu diesen Beispielen zeigen "w" für Breite.

3. Finden Sie die Länge des Balkens. Die Länge ist die längste Seite des Balkens, die parallel zum Boden oder der Oberfläche ist, auf der er ruht. Die Länge ist möglicherweise bereits auf dem Bild angegeben oder muss mit einem Lineal gemessen werden.

4. Finden Sie die Breite des Balkens. Die Breite des Balkens kann durch Messen der kurzen Seite, die parallel zum Boden oder der Oberfläche ist, auf der er ruht, ermittelt werden. Überprüfe auch hier zuerst, ob es bereits auf dem Bild angegeben ist, und messe es ansonsten mit deinem Lineal aus.

5. Finden Sie die Höhe des Balkens. Höhe ist der Abstand vom Boden oder der Oberfläche, auf der der Balken auf der Oberseite des Balkens ruht. Sehen Sie, ob es auf dem Bild bereits angezeigt ist und messen Sie es anders mit Ihrem Lineal oder Maßband.

6. Gib die Maße in die Formel ein und berechne sie. Denken Sie daran, dass V = l x w x h.

7. Schreiben Sie Ihre Antwort unbedingt in Kubikzentimetern. Das Ergebnis sind also 72 Kubikzentimeter oder 72 cm³.
Methode 3 von 6: Berechnung des Volumens eines Zylinders

1. Erfahren Sie, wie Sie einen Zylinder identifizieren. Ein Zylinder ist eine dreidimensionale Form mit zwei identischen runden Enden, die durch eine einzige gekrümmte Seite verbunden sind. Es ist eigentlich ein gerader, runder Stab.
- Eine Dose ist ein gutes Beispiel für einen Zylinder oder eine AA-Batterie.

2. Merken Sie sich die Formel für das Volumen eines Zylinders. Um das Volumen eines Zylinders zu berechnen, müssen Sie seine Höhe und den Radius seiner kreisförmigen Grundfläche kennen.Der Radius ist der Abstand vom Mittelpunkt des Kreises zum Rand. Die Formel lautet V =π x r² x h, wobei V das Volumen, r der Radius, h die Höhe und π die Konstante pi . ist.

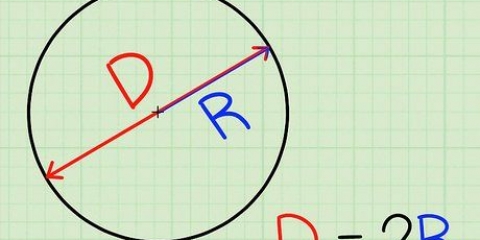
3. Finden Sie den Radius der Basis. Wenn es bereits auf dem Bild angegeben ist, einfach ausfüllen. Wenn Sie den Durchmesser anstelle des Radius erhalten, teilen Sie ihn einfach durch 2, um den Radius zu finden (d = 2 x r).

4. Messen Sie die Form, wenn der Radius nicht angegeben ist. Beachten Sie, dass es schwierig sein kann, den genauen Radius eines Kreises zu messen. Eine Möglichkeit besteht darin, den Kreis an seiner breitesten Stelle mit dem Lineal von oben nach unten zu messen und durch zwei zu teilen.

5. Berechnen Sie die Fläche des Kreises an der Basis. Setzen Sie den Radius in die Formel π x r² . ein. Multiplizieren Sie den Radius mit sich selbst und multiplizieren Sie das Ergebnis mit π. Zum Beispiel:

6. Finden Sie die Höhe des Zylinders. Dies ist einfach der Abstand zwischen den beiden kreisförmigen Basen oder der Abstand von der Oberfläche, auf der der Zylinder aufliegt, bis zur Oberseite des Zylinders. Sehen Sie, ob die Länge bereits auf dem Bild angegeben ist, oder messen Sie sie anders mit Ihrem Lineal oder Maßband.

7. Multiplizieren Sie die Fläche der Basis mit der Höhe des Zylinders, um das Volumen zu finden. Setze die Werte in die Formel V =π x r² x h. In unserem Beispiel mit einem Radius von 4 cm und einer Höhe von 10 cm:

8. Denken Sie daran, Ihre Antwort in Kubikzentimetern zu schreiben. In diesem Beispiel wurde der Zylinder in Zentimetern gemessen, daher muss die Antwort in Kubikzentimetern geschrieben werden: V = 502,4 cm³. Wenn der Zylinder in Metern gemessen würde, müsste das Volumen in Quadratmetern (m³) geschrieben werden.
Methode 4 von 6: Berechnung des Volumens einer regelmäßigen Pyramide

1. Wissen, was eine regelmäßige Pyramide ist. Eine Pyramide ist eine dreidimensionale Form mit einem Polygon an der Basis und Seiten, die sich nach oben verjüngen (die Spitze der Pyramide).Eine regelmäßige Pyramide ist eine Pyramide, deren Grundfläche ein regelmäßiges Vieleck ist, was bedeutet, dass alle Seiten und Winkel dieses Vielecks gleich sind.
- Normalerweise wird eine Pyramide mit einer quadratischen Grundfläche und spitz zulaufenden Seiten dargestellt, aber die Grundfläche einer Pyramide kann tatsächlich 5, 6 oder 100 Seiten haben!
- Eine Pyramide mit einem Kreis als Basis wird Kegel genannt, was wir in der nächsten Methode besprechen werden.

2. Lerne die Formel zur Berechnung des Volumens der regelmäßigen Pyramide. Die Formel für das Volumen einer regelmäßigen Pyramide lautet V = 1/3 x b x h, wobei b die Fläche der Basis und h die Höhe der Pyramide oder der vertikale Abstand von der Basis zur Spitze ist.

3. Berechnen Sie die Fläche der Basis. Die Formel dafür hängt von der Seitenzahl der Basis ab. In unserem Beispiel ist die Basis ein Quadrat mit einer Seitenlänge von 6 cm. Denken Sie daran, dass die Formel zur Berechnung der Fläche eines Quadrats A = s² . ist. Bei unserer Pyramide also 6 x 6 = 36 cm².

4. Finden Sie die Höhe der Pyramide. In den meisten Fällen wird es auf dem Bild angezeigt. In unserem Beispiel beträgt die Höhe der Pyramide 10 cm.

5. Multiplizieren Sie die Fläche der Basis der Pyramide mit der Höhe und dividieren Sie durch 3, um das Volumen zu ermitteln. Denken Sie daran, dass die Formel V = 1/3 x b x h . lautet. In unserem Beispiel hat die Pyramide eine Grundfläche mit einer Fläche von 36 und einer Höhe von 10, das Volumen beträgt also 36 x 10 x 1/3 = 120.

6. Denken Sie daran, das Ergebnis in Kubikeinheiten zu schreiben. Die Maße der Pyramide im Beispiel wurden in Zentimetern angegeben, das Ergebnis muss also in Kubikzentimetern geschrieben werden, 120 cm³. Wenn die Maße in Metern angegeben wurden, schreiben Sie die Antwort in Kubikmeter (m³).
Methode 5 von 6: Berechnung des Volumens eines Kegels

1. Erfahren Sie, was die Eigenschaften eines Kegels sind. Ein Kegel ist eine dreidimensionale Form mit einer kreisförmigen Basis und einem einzelnen Punkt auf der gegenüberliegenden Seite. Eine andere Möglichkeit, einen Kegel zu sehen, ist, dass es sich um eine besondere Art von Pyramide mit kreisförmiger Basis handelt.
- Befindet sich die Spitze des Kegels direkt über der Mitte der Basis, spricht man von einem geraden Kegel. Liegt er nicht direkt über dem Zentrum, wird er als schräger Kegel bezeichnet. Glücklicherweise ist die Formel zur Berechnung des Volumens für beide Kegeltypen gleich.

2. Kennen Sie die Formel zur Berechnung des Volumens des Kegels. Diese Formel lautet V = 1/3 x π x r² x h, wobei r der Radius des Kreises an der Basis ist, h die Höhe des Kegels und π die Konstante pi ist, die auf 3,14 . gerundet werden kann.

3. Berechnen Sie die Fläche der kreisförmigen Basis des Kegels. Dazu müssen Sie den Radius der Basis kennen, der auf Ihrem Bild angegeben sein sollte. Wenn Sie den Durchmesser anstelle des Radius erhalten, teilen Sie diese Zahl einfach durch 2, da der Durchmesser das 2-fache des Radius ist (d = 2 x r). Setzen Sie dann den Radius in die Formel A = π x r² ein, um die Fläche zu berechnen.

4. Finden Sie die Höhe des Kegels. Dies ist der vertikale Abstand von der Basis des Kegels nach oben. In unserem Beispiel beträgt die Höhe des Kegels 5 cm.

5. Multiplizieren Sie die Höhe des Kegels mit der Fläche der Basis. In unserem Beispiel beträgt die Grundfläche 28,27 cm² und die Höhe 5 cm, also B x H = 28,27 x 5 = 141,35.

6. Jetzt multiplizieren Sie dieses Ergebnis mit 1/3 (oder dividieren durch 3), um das Volumen des Kegels zu erhalten. Im obigen Schritt haben wir tatsächlich das Volumen eines Zylinders berechnet, dh eines Kegels, bei dem die Wände aufrecht stehen und in einem anderen Kreis enden würden. Wenn du es durch 3 teilst, erhältst du das Volumen des Kegels.

7. Denken Sie daran, das Ergebnis in Kubikeinheiten zu schreiben. Unser Kegel wurde in Zentimetern gemessen, daher sollte das Volumen in Kubikzentimetern ausgedrückt werden: 47,12 cm³.
Methode 6 von 6: Berechnung des Volumens einer Kugel

1. Erkenne eine Kugel. Eine Kugel ist eine perfekt runde dreidimensionale Form, bei der jeder Punkt auf ihrer Oberfläche gleich weit vom Zentrum entfernt ist. Mit anderen Worten, es ist ein Ball.

2. Lernen Sie die Formel zur Berechnung des Volumens einer Kugel. Die Formel lautet V = 4/3 x π x r³ (dh: "vier Drittel pi mal kubischer r"), wobei r der Radius der Kugel ist und π die Konstante pi ist (3.14).

3. Finden Sie den Radius der Kugel. Wenn der Radius bereits im Bild angegeben ist, ist es einfach. Bei gegebenem Durchmesser dividiere diese Zahl durch 2, um den Radius zu erhalten. Der Radius der Kugel beträgt in diesem Beispiel 3 Zentimeter.

4. Messen Sie die Kugel, wenn der Radius nicht angegeben ist. Wenn Sie eine Kugel (z. B. einen Tennisball) messen müssen, um den Radius zu bestimmen, finden Sie eine Schnur, die lang genug ist, um sie vollständig zu umwickeln. Wickeln Sie es dann an der breitesten Stelle um das Objekt und markieren Sie die Stelle, an der die Saite wieder zusammenkommt. Messen Sie dann diesen Teil der Schnur mit einem Lineal, um den Umfang der Kugel zu ermitteln. Teilen Sie das durch 2 x π oder 6,28, dann kennen Sie den Radius.

5. Erhöhe den Radius in die dritte Potenz, um r³ . zu finden. Die dritte Potenz bedeutet einfach, die Zahl dreimal mit sich selbst zu multiplizieren, also r³ = r x r x r. In unserem Beispiel r=3 wird daraus 3 x 3 x 3 = 27.

6. Multiplizieren Sie Ihre Antwort mit 4/3. Du kannst es mit einem Taschenrechner machen oder einfach selbst machen und den Bruch vereinfachen. In unserem Beispiel ist es 27 x 4/3 = 180/3 oder 36.

7. Multiplizieren Sie das Ergebnis mit π, um das Volumen der Kugel zu finden. Der letzte Schritt bei der Berechnung des Volumens besteht darin, das bisherige Ergebnis mit π . zu multiplizieren. Runden Sie π auf zwei Dezimalstellen, das reicht für die meisten Matheaufgaben (es sei denn, Ihr Lehrer sagt etwas anderes), also multiplizieren Sie es mit 3,14 und Sie haben Ihre Antwort.

8. Schreiben Sie Ihre Antwort in Kubikeinheiten. In unserem Beispiel haben wir in Zentimetern gemessen, also lautet die Antwort V = 113,09 cm³.
Оцените, пожалуйста статью