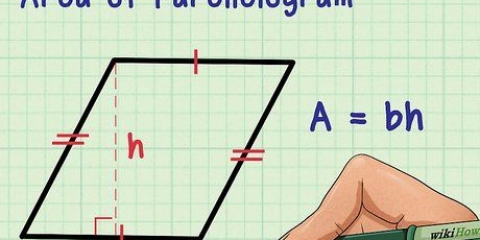Die Fläche eines Vierecks berechnen

Schritte

Für deine Hausaufgaben musst du also die Fläche eines Vierecks berechnen...Aber du hast nicht einmal eine Ahnung, was ein Viereck ist. Keine Panik – die Rettung ist nah! Ein Viereck ist jede Figur, die aus 4 Seiten/Winkeln besteht. Sie müssen lediglich den Vierecktyp des Problems bestimmen und die entsprechende Formel verwenden, um die Fläche zu berechnen.

Schritte

Methode 1 von 4: Quadrate, Rechtecke und andere Parallelogramme

1. Erfahren Sie, wie Sie bestimmen, was ein Parallelogramm ist. Ein Parallelogramm ist ein Viereck mit 2 Paaren paralleler Seiten, wobei die parallelen Seiten gleich lang sind. Quadrate, Rechtecke und Rauten sind alle Parallelogramme.

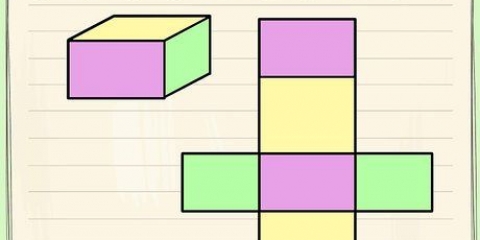
2. Finden Sie die Fläche eines Quadrats. Da jede Seite eines Quadrats gleich lang ist, müssen Sie nur die Länge einer Seite messen (nennen Sie es "T"), um die Fläche eines Quadrats zu finden. Dies entspricht der Multiplikation der Grundfläche des Quadrats mit seiner Höhe; die basis und die höhe sind immer gleich. Verwenden Sie die folgende Formel:

K = t

Dies ist dasselbe wie K = t * t

Wenn eine Seite eines Quadrats eine Länge von 4 hat (t = 4), dann ist die Fläche t oder 4 x 4 = 16.

3. Finden Sie die Fläche eines Rechtecks. Um die Fläche eines Rechtecks zu finden, muss man die Länge und Breite des Rechtecks kennen. Die Formel lautet wie folgt:

K = b*h

Wenn die Länge 10 und die Breite 5 beträgt, beträgt die Fläche des Rechtecks 10 x 5 (l * b) = 50.

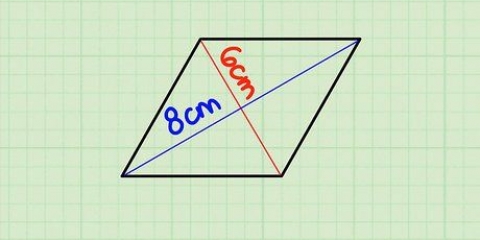
4. Finden Sie die Fläche eines Quadrats. Das kann knifflig sein – man kann hier nicht einfach eine Seite mit der anderen multiplizieren. Sie müssen nun von jedem Punkt Linien ziehen und die Diagonalen der Form messen, falls nicht angegeben. Dann multiplizieren Sie die Diagonalen wie folgt:

K = (b*h)/2, für die b = Diagonale 1 und h = Diagonale 2

Wenn ein Quadrat Diagonalen der Länge 6 dann 8 hat, dann ist die Fläche (6 x 8)/2 = 48/2 = 24

Methode 2 von 4: Die Fläche eines Trapezes

1. Bestimmen Sie, ob es ein Trapez ist. Ein Trapez ist ein Viereck mit mindestens 2 parallelen Seiten. Jede der vier Seiten eines Trapezes kann eine andere Länge haben. Es gibt zwei verschiedene Möglichkeiten, die Fläche eines Trapezes zu finden, abhängig von den gemachten Angaben.

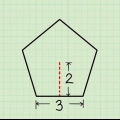
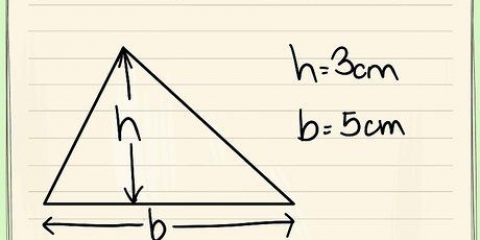
2. Bestimmen Sie die Höhe des Trapezes. Die Höhe eines Trapezes ist die senkrechte Linie, die die obere Grundlinie und die untere Grundlinie verbindet, und Sie benötigen beide, um die Fläche zu berechnen. Das ist nicht gleich lang wie eine der Seiten, da jede Seite diagonal ist. So finden Sie die Höhe:

Bestimmen Sie, was die kürzeste Basis ist. Platzieren Sie Ihren Bleistift in der Ecke zwischen der Grundlinie und ziehen Sie eine Linie gerade nach oben oder unten zur anderen Grundlinie. Sie sollten jetzt ein Dreieck mit einem Winkel von 90 Grad gezeichnet haben.

Verwenden Sie Trigonometrie, um die Höhe zu bestimmen. Wenn Sie beispielsweise die Länge einer Seite und den angrenzenden Winkel kennen und das Dreieck einen 90-Grad-Winkel hat, dann ist die Höhe die Länge der Seite mal dem Sinus des Winkels.

Angenommen, die Höhe des Trapezes beträgt 10.

3. Bestimmen Sie die Fläche des Trapezes anhand der Höhe und Länge der Basis. Wenn Sie die Höhe des Trapezes und die Länge der beiden Grundseiten kennen, verwenden Sie die folgende Formel:

K = (a+b)/2 * h

Wenn die Höhe 10 ist und die Basis eine Länge von 7 und 9 hat, können Sie die Fläche durch folgende Berechnung ermitteln: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Finden Sie die Fläche eines Trapezes mit dem Mittelsegment. Dieses Mittelsegment ist eine Linie, die parallel zur unteren und oberen Linie des Trapezes verläuft und eine Länge genau dazwischen hat. So arbeiten Sie:

Bestimmen Sie das mittlere Segment. Um die Länge des Mittelsegments zu bestimmen m, wir nehmen den Durchschnitt der Seitenlängen ein und B (oder die untere und obere Linie des Trapezes).Verwenden Sie die Formel: m = (a+b)/2.Da Sie nun die Länge des Mittelsegments kennen, können Sie es mit der Höhe multiplizieren, um die Fläche zu ermitteln. Verwenden Sie die folgende Formel:

K = m*h

Dies ist im Wesentlichen die gleiche Formel wie das Original, ersetzt aber jetzt "m" der Term (a + b)/2.

Angenommen, Sie kennen das mittlere Segment dieses Trapezes. Angenommen, dies ist 8, dann ist die Fläche des Trapezes 8 x 10 = 80, genau wie bei der vorherigen Methode.

Methode 3 von 4: Bestimmung der Oberfläche eines Drachens

1. Was ist ein Drachen?. Ein Drachen ist definiert als eine geometrische Form, bei der 2 Paare gleichlanger Seiten miteinander verbunden sind, was einem normalen Drachen ähnelt. Es gibt zwei verschiedene Möglichkeiten, die Fläche dieser Figur zu finden, abhängig von den gemachten Angaben.

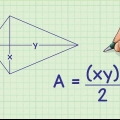
2. Ermitteln Sie die Fläche eines Drachens anhand der Länge seiner Seiten. Wenn Sie die Länge von zwei verschiedenen Seiten eines Drachens kennen und den Winkel zwischen diesen Seiten kennen, verwenden Sie die folgende Formel, wobei der Winkel gleich Theta (θ) ist:

K =(a*b) * sin θ

3. Finden Sie die Fläche eines Drachens mithilfe der Diagonalen. Eine Diagonale ist die gerade Linie zwischen zwei gegenüberliegenden Ecken des Drachens. Jeder Drachen hat 2 Diagonalen.

Bestimmen Sie die Länge jeder Diagonale. Zeichne eine Linie von einer Ecke eines Drachens zur gegenüberliegenden. Sie sollten jetzt 2 Dreiecke haben. Bestimmen mit Dieser Beitrag, Wie lang ist die Diagonale (die drei Winkel eines Dreiecks ergeben zusammen 180 Grad).

Nachdem Sie die erste Diagonale bestimmt haben, verwenden Sie die gleichen Prinzipien, um die Länge der anderen zu bestimmen. Verwenden Sie dann diese Formel, um die Fläche zu bestimmen, in der P und Q stellen die Länge der Diagonalen dar:

K = (p*q)/2

Wenn die Diagonalen die Längen 4 und 6 haben, dann ermittelst du die Fläche des Drachens wie folgt: (4 x 6)/2 = 24/2 = 12

Beachten Sie, dass diese Formel auch für die Fläche einer Raute funktioniert, da dies eine spezielle Art von Drachen ist, bei der alle Seiten gleich lang sind.

Methode 4 von 4: Eine allgemeine Formel

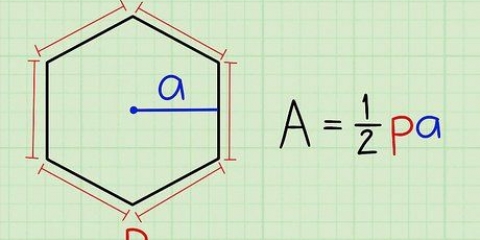
1. Die allgemeine Formel zur Bestimmung der Fläche eines Vierecks. Es gibt Formeln, um die Fläche jedes Vierecks zu bestimmen, unabhängig von seiner Form. Hier ist die allgemeinste Form nach trigonometrischen Prinzipien:

wenn k ist die Gesamtfläche des Vierecks, ein, B, C und D repräsentieren die Längen der 4 Seiten, ein ist der Winkel (in Grad) zwischen den Seiten ein und D und C ist der Winkel (in Grad) zwischen den Seiten B und C, dann:
K = 0.5*a*d * sin A + 0.5*b*c * sin C
Wenn Sie versuchen, die Fläche eines Parallelogramms zu finden, in der die entgegengesetzten Winkel gleich sind, wird die Formel einfacher: K = 0.5*(ad + bc) * sin A.