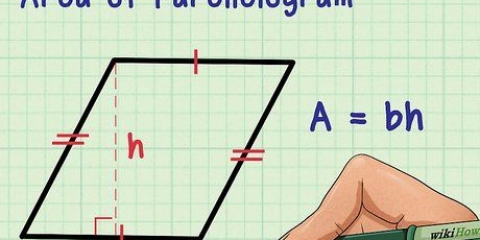Fläche berechnen

Schritte
Notwendigkeiten

Fläche ist die Gesamtfläche, die von allen Flächen eines Objekts eingenommen wird. Es ist die Summe aller Bereiche dieses Objekts. Die Bestimmung der Fläche einer dreidimensionalen Form ist ziemlich einfach, solange Sie die richtige Formel verwenden. Jede Form hat ihre eigene separate Formel, daher müssen Sie zuerst überprüfen, um welche Form es sich handelt. Die Berechnung der Flächenformel für verschiedene Objekte kann die Berechnungen in Zukunft erleichtern. Hier besprechen wir einige der gängigsten Formen, denen Sie begegnen können.

Schritte

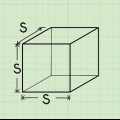
Methode 1 von 7: Würfel

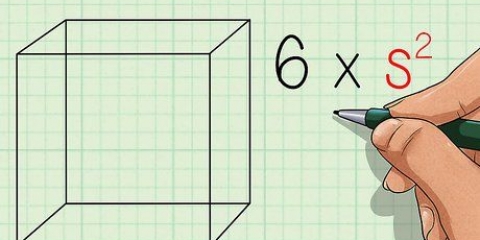
1. Definiere die Formel für die Fläche eines Würfels. Ein Würfel hat sechs identische Seiten. Da sowohl die Länge als auch die Breite eines Quadrats gleich sind, ist die Fläche eines Quadrats ein, wodurch ein die länge ist eine seite. Da ein Würfel sechs gleiche Flächen hat, können Sie seine Fläche berechnen, indem Sie die Fläche einer seiner Flächen mit sechs multiplizieren. Die Formel für die Fläche eines Würfels O lautet O = 6a, wodurch ein die länge ist eine seite.

Die Einheit der Fläche ist eine bestimmte Länge zum Quadrat: cm, dm, m, etc.

2. Messen Sie die Länge einer Seite. Per Definition sollte jede Seite oder Kante (Kante) eines Würfels gleich der anderen sein, sodass Sie nur eine Seite messen müssen. Messen Sie die Länge der Seite mit einem Lineal. Achten Sie auf die von Ihnen verwendeten Einheiten.

Notieren Sie diese Messung als ein.

Beispiel: a = 2 cm

3. Quadrieren Sie Ihre Messung für ein. Quadrieren Sie das Maß, um die Länge der Rippe zu berechnen. Einen Wert quadrieren bedeutet, ihn mit sich selbst zu multiplizieren. Wenn Sie dies zum ersten Mal lernen, kann es nützlich sein, sich daran zu erinnern, da NT= 6*a*a.

Beachten Sie, dass dieser Schritt die Fläche einer Fläche des Würfels berechnet.

Beispiel: a = 2 cm

a = 2 x 2 = 4 cm

4. Multiplizieren Sie dieses Produkt mit sechs. Denken Sie daran, dass ein Würfel sechs identische Flächen hat. Jetzt, da Sie die Fläche eines der Gesichter kennen, multiplizieren Sie ihn mit sechs (wegen aller sechs Gesichter).

Dieser Schritt schließt die Berechnung der Fläche des Würfels ab.

Beispiel: a = 4 cm

Fläche = 6 x a = 6 x 4 = 24 cm

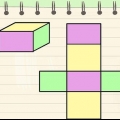
Methode 2 von 7: Rechteckiges Prisma

1. Definieren Sie die Formel für die Fläche eines rechteckigen Prismas. Wie ein Würfel hat ein rechteckiges Prisma sechs Flächen, aber im Gegensatz zu einem Würfel sind diese Flächen nicht gleich. In einem rechteckigen Prisma sind nur die gegenüberliegenden Seiten gleich. Daher müssen bei der Berechnung der Fläche eines rechteckigen Prismas die verschiedenen Längen der Rippen wie in der Formel berücksichtigt werden SA = 2ab + 2bc + 2ac.

Für diese Formel gilt ein gleich der Breite des Prismas, B gleich der Höhe und C gleich der Länge.
Wenn wir uns die Formel genauer ansehen, werden Sie feststellen, dass wir einfach alle Flächen jeder Fläche des Objekts addieren.
Die Flächeneinheit ist eine bestimmte Länge zum Quadrat: cm, dm, m usw.

2. Messen Sie die Länge, Höhe und Breite jeder Seite. Alle drei Messwerte können unterschiedlich sein, daher muss jeder separat gemessen werden. Messen Sie jede Seite mit einem Lineal und notieren Sie den Wert. Verwenden Sie für jede Messung die gleichen Einheiten.

Messen Sie die Länge der Basis, um die Länge des Prismas zu bestimmen, und weisen Sie es zu C.

Beispiel: c = 5 cm

Messen Sie die Breite der Basis, um die Breite des Prismas zu bestimmen, und nennen Sie es ein.

Beispiel: a = 2 cm

Messen Sie die Höhe der Seite, um die Höhe des Prismas zu bestimmen, und nennen Sie es B.

Beispiel: b = 3 cm

3. Berechnen Sie die Fläche einer der Flächen des Prismas und multiplizieren Sie sie mit zwei. Denken Sie daran, dass ein rechteckiges Prisma sechs Flächen hat und die gegenüberliegenden Flächen einander gleich sind. Länge und Höhe multiplizieren, oder C und ein, um die Fläche eines Flugzeugs zu finden. Nehmen Sie diese Messung vor und multiplizieren Sie sie mit zwei, um die gegenüberliegende identische Ebene zu berücksichtigen.

Beispiel: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm

4. Finden Sie die Fläche der anderen Seite des Prismas und multiplizieren Sie sie mit zwei. Multiplizieren Sie wie beim ersten Satz von Flächen die Breite und Höhe, oder ein und B zur Bestimmung der Fläche einer anderen Fläche des Prismas. Multiplizieren Sie diese Messung mit zwei, um die gegenüberliegenden identischen Seiten zu berücksichtigen.

Beispiel: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm

5. Berechnen Sie die Fläche der Enden des Prismas und multiplizieren Sie sie mit zwei. Die anderen beiden Seiten des Prismas sind die Enden. Länge und Breite multiplizieren (C und B) um ihre Oberfläche zu finden. Multiplizieren Sie diesen Bereich mit zwei, um beide Seiten zu berücksichtigen.

Beispiel: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm

6. Füge die drei separaten Bereiche zusammen. Da die Fläche des Prismas die Gesamtfläche aller Flächen eines Objekts ist, besteht der letzte Schritt darin, alle individuell berechneten Flächen zu addieren. Addiere die Flächen aller Seiten zusammen, um die Gesamtfläche zu erhalten.

Beispiel: Fläche = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm.

Methode 3 von 7: Dreiecksprisma

1. Definieren Sie die Flächenformel für ein Dreiecksprisma. Ein dreieckiges Prisma hat zwei identische dreieckige Flächen und drei rechteckige Flächen. Um die Fläche zu finden, musst du die Fläche aller Gesichter berechnen und sie zusammenzählen. Die Fläche eines dreieckigen Prismas ist SA = 2A + PH, wobei A die Fläche der dreieckigen Basis ist, P der Umfang der dreieckigen Basis ist und h die Höhe des Prismas ist.

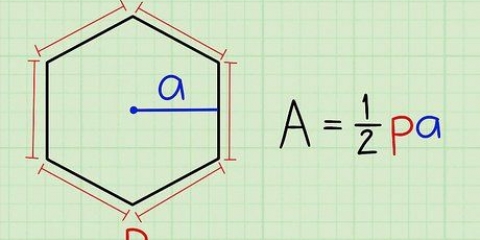
Für diese Formel gilt, dass ein das Fläche eines Dreiecks und somit A = 1/2bh, wodurch B ist die Basis des Dreiecks und h die Höhe.
P ist der Umfang des Dreiecks, der durch Addition aller drei Kanten des Dreiecks berechnet wird.
Die Flächeneinheit ist eine Längeneinheit zum Quadrat: cm, dm, m usw.

2. Berechnen Sie die Fläche der dreieckigen Ebene und multiplizieren Sie sie mit zwei. Die Fläche eines Dreiecks ist /₂b*h wobei b die Basis des Dreiecks und h die Höhe ist. Da es also zwei identische Dreiecke als Flächen gibt, multiplizieren wir die Formel mit zwei. Dies macht die Berechnung für beide Ebenen einfach (b*h).

Die Basis B, ist gleich der Länge der Unterseite des Dreiecks.

Beispiel: b = 4 cm

Die Höhe h der dreieckigen Basis ist gleich dem Abstand zwischen Unterkante und Spitze.

Beispiel: h = 3 cm²

Die Fläche eines Dreiecks multipliziert mit 2 = 2(1/2)b*h = b*h = 4*3 = 12 cm

3. Messen Sie jede Seite des Dreiecks und die Höhe des Prismas. Um die Flächenberechnung abzuschließen, müssen Sie die Länge jeder Seite des Dreiecks und die Höhe des Prismas kennen. Die Höhe ist der Abstand zwischen den beiden Dreiecksflächen.

Beispiel: H = 5 cm²

Die drei Seiten beziehen sich auf die drei Seiten der dreieckigen Basis.

Beispiel: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm

4. Finden Sie den Umfang des Dreiecks. Der Umfang des Dreiecks kann berechnet werden, indem alle gemessenen Seiten zusammengezählt werden: S1 + S2 + S3.

Beispiel: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm

5. Multiplizieren Sie den Umfang der Basis mit der Höhe des Prismas. Denken Sie daran, dass die Höhe des Prismas der Abstand zwischen den beiden Dreiecksflächen ist. Mit anderen Worten, multiplizieren Sie P von huh.

Beispiel: P x H = 12 x 5 = 60 cm²

6. Addieren Sie die beiden separaten Messwerte zusammen. Sie müssen die beiden Messungen aus den vorherigen beiden Schritten addieren, um die Fläche des Dreiecksprismas zu erhalten.

Beispiel: 2A + PH = 12 + 60 = 72 cm.

Methode 4 von 7: Bol

1. Definieren Sie die Flächenformel für eine Kugel. Eine Kugel hat eine gekrümmte Oberfläche, daher ist die Oberfläche ein Wert multipliziert mit der Konstanten pi. Die Fläche einer Kugel wird mit der Gleichung berechnet NT = 4π*r.

Für diese Formel gilt R gleich dem Radius der Kugel. Pi (oder π) kann auf 3,14 . gerundet werden.
Die Einheiten der Fläche sind eine Längeneinheit im Quadrat: cm, dm, m usw.

2.Messen Sie den Radius der Glühbirne. Der Radius der Kugel ist der halbe Durchmesser bzw. der Abstand vom Kugelmittelpunkt zum Rand.

Beispiel: r = 3 cm

3. Den Radius quadrieren. Um eine Zahl zu quadrieren, multipliziere sie mit sich selbst. Multiplizieren Sie die Messung mit R mit sich selbst. Denken Sie daran, dass diese Formel umgeschrieben werden kann als SA = 4π*r*r.

Beispiel: r = r x r = 3 x 3 = 9 cm

4. Multiplizieren Sie den quadrierten Radius mit einer Rundung von Pi. Pi ist eine Konstante, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser darstellt. Es ist eine irrationale Zahl mit vielen Nachkommastellen. Es wird oft auf 3,14 . gerundet. Multiplizieren Sie den quadrierten Radius mit π oder 3,14 für die Fläche eines kreisförmigen Querschnitts der Kugel.

Beispiel: π*r = 3,14 x 9 = 28,26 cm

5. Multiplizieren Sie dieses Produkt mit vier. Um die Berechnung abzuschließen, multiplizieren Sie sie mit vier. Finden Sie die Fläche der Kugel, indem Sie die flache Kreisfläche mit vier multiplizieren.

Beispiel: 4π*r = 4 x 28,26 = 113,04 cm

Methode 5 von 7: Zylinder

1. Definieren Sie die Flächenformel für einen Zylinder. Ein Zylinder hat zwei kreisförmige Enden, die eine röhrenförmige Oberfläche schließen. Die Formel für die Fläche eines Zylinders lautet NT = 2π*r + 2π*rh, wodurch R gleich dem Radius der kreisförmigen Basis und h entspricht der Höhe des Zylinders. runden Pi (oder π) sinkt auf 3,14.

Die Formel 2π*r berechnet die Fläche der beiden kreisförmigen Enden, während 2πrh die Fläche der Säule zwischen den beiden Enden ist.
Die Flächeneinheiten sind eine Längeneinheit zum Quadrat: cm, dm, m usw.

2. Messen Sie den Radius und die Höhe des Zylinders. Der Radius eines Kreises ist der halbe Durchmesser oder der Abstand vom Kreismittelpunkt zum Rand. Die Höhe ist der Gesamtabstand des Zylinders von einem Ende zum anderen. Zeichne diese Maße mit einem Lineal und schreibe sie auf.

Beispiel: r = 3 cm

Beispiel: h = 5 cm

3. Finden Sie die Fläche der Basis und multiplizieren Sie sie mit zwei. Um die Fläche der Basis zu finden, verwenden Sie die Flächenformel oder einen Kreis (π*r). Um die Berechnung abzuschließen, quadrieren Sie den Radius und multiplizieren Sie ihn mit Pi. Dann mit zwei multiplizieren wegen des zweiten identischen Kreises am anderen Ende des Zylinders.

Beispiel: Grundfläche = π*r = 3,14 x 3 x 3 = 28,26 cm

Beispiel: 2π*r = 2 x 28,26 = 56,52 cm

4. Berechnen Sie die Oberfläche des Zylinders selbst mit 2π*rh. Dies ist die Formel zur Berechnung der Fläche einer Röhre. Das Rohr ist der Raum zwischen den beiden kreisförmigen Enden des Zylinders. Multiplizieren Sie den Radius mit zwei, Pi und die Höhe.

Beispiel: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm

5. Addieren Sie die beiden separaten Messwerte zusammen. Addiere die Fläche der beiden Kreise zur Fläche des Raums zwischen den beiden Kreisen, um die Gesamtfläche des Zylinders zu berechnen. Hinweis: Beim Hinzufügen dieser beiden Teile erkennen Sie die Originalformel: NT = 2π*r + 2π*rh.

Beispiel: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm

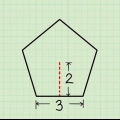
Methode 6 von 7: Quadratische Pyramide

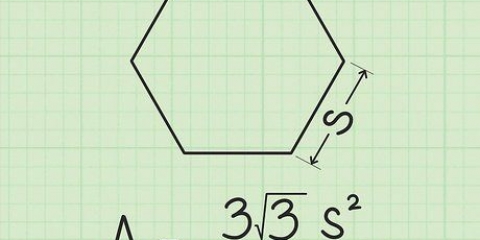
1. Definiere die Flächenformel für eine quadratische Pyramide. Eine quadratische Pyramide hat eine quadratische Grundfläche und vier dreieckige Seiten. Wie bereits erwähnt, ist die Fläche eines Quadrats die Länge einer Seite zum Quadrat. Die Fläche eines Dreiecks beträgt 1/2sl (die Seite des Dreiecks mal die Länge oder Höhe des Dreiecks). Da es vier Dreiecke gibt, berechnen Sie die Gesamtfläche, indem Sie diese mit vier multiplizieren. Die Addition all dieser Flächen ergibt die Flächengleichung für eine quadratische Pyramide: NT = s + 2ch.

In dieser Gleichung S die Länge jeder Seite der quadratischen Basis und l die schräge Höhe jeder dreieckigen Seite.
Die Flächeneinheit ist eine bestimmte Längeneinheit zum Quadrat: cm, dm, m usw.

2. Messen Sie die geneigte Höhe und die Basisseite. Die schräge Höhe l, ist die Höhe einer der dreieckigen Seiten. Es ist der Abstand von der Basis zur Spitze der Pyramide, gemessen entlang einer flachen Seite. Die grundlegende Seite S, ist die Länge einer Seite der quadratischen Grundfläche. Da die Grundfläche quadratisch ist, ist dieses Maß für alle Seiten gleich. Verwenden Sie für jede Messung ein Lineal.

Beispiel: l = 3 cm²

Beispiel: s = 1 cm

3. Finden Sie die Fläche der quadratischen Grundfläche. Die Fläche einer quadratischen Grundfläche kann berechnet werden, indem man die Länge einer Seite quadriert (S mit sich selbst multiplizieren).

Beispiel: s = s x s = 1 x 1 = 1 cm

4. Berechnen Sie die Gesamtfläche der vier Dreiecksflächen. Der zweite Teil der Gleichung ist die Fläche der verbleibenden vier Dreiecksflächen. Mit der Formel 2ls multiplizieren wir S von l und zwei. Finden Sie den Bereich jedes Gesichts.

Beispiel: 2 x s x l = 2 x 1 x 3 = 6 cm

5. Füge die beiden getrennten Bereiche zusammen. Addiere die Gesamtfläche der Gesichter zur Fläche der Basis, um die Gesamtfläche zu berechnen.

Beispiel: s + 2 Kanäle = 1 + 6 = 7 cm

Methode 7 von 7: Kegel

1. Definiere die Flächenformel für einen Kegel. Ein Kegel hat eine runde Basis und eine runde Oberfläche, die sich spitz zuläuft. Um die Fläche zu finden, nimm die Fläche der kreisförmigen Basis und die Fläche des Kegels und addiere die beiden zusammen. Die Formel für die Fläche eines Kegels lautet: SA = *r + π*rl, wodurch R der Radius ist von der kreisförmigen Basis, l die schräge Höhe des Kegels und π die Konstante pi (3.14).

Die Flächeneinheit ist eine bestimmte Längeneinheit zum Quadrat: cm, dm, m usw.

2. Messen Sie den Radius und die Höhe des Kegels. Der Radius ist der Abstand von der Mitte der kreisförmigen Grundfläche zum Rand der Grundfläche. Höhe ist der Abstand von der Mitte der Basis bis zur Spitze des Kegels, gemessen durch die Mitte des Kegels.

Beispiel: r = 2 cm

Beispiel: h = 4 cm

3. Berechnen Sie die Hanghöhe (l) des Kegels. Da die schräge Höhe die tatsächliche Hypotenuse eines Dreiecks ist, müssen Sie die mit dem Satz des Pythagoras um es zu berechnen. Verwenden Sie die neu angeordnete Form, l = √ (r + h), wodurch R der Radius ist und h die Höhe des Kegels.

Beispiel: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm

4. Finden Sie die Fläche der kreisförmigen Basis. Die Fläche der Basis wird mit der Formel π*r . berechnet. Nachdem Sie den Radius gemessen haben, quadrieren Sie ihn (also multiplizieren Sie ihn mit sich selbst) und dann multiplizieren Sie dieses Produkt mit pi.

Beispiel: π*r = 3,14 x 2 x 2 = 12,56 cm

5. Berechnen Sie die Fläche der Spitze des Kegels. Verwenden Sie die Formel π*rl, wobei R der Radius ist vom Kreis und l die oben berechnete Neigung, um die Fläche der Spitze des Kegels zu bestimmen.

Beispiel: π*rl = 3,14 x 2 x 4,47 = 28,07 cm

6. Addiere die beiden Bereiche zusammen, um die Gesamtfläche des Kegels zu erhalten. Berechnen Sie die endgültige Fläche des Kegels, indem Sie bei der Berechnung des vorherigen Schritts die Fläche der kreisförmigen Basis addieren.

Beispiel: *r + π*rl = 12,56 + 28,07 = 40,63 cm