Die Fläche eines gleichschenkligen Dreiecks berechnen (mit Bildern)

Schritte
- Methode 1 von 2: Bestimmen der Fläche anhand der Längen jeder Seite
- Methode 2 von 2: Verwenden von Trigonometrie
Tipps

Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten. Diese beiden gleichen Seiten haben immer den gleichen Winkel zur Basis (der dritten Seite) und treffen sich direkt über der Mitte der Basis. Mit einem Lineal und zwei gleichlangen Bleistiften können Sie das selbst testen: Wenn Sie versuchen, das Dreieck in eine Richtung zu neigen, treffen sich die Enden der Bleistifte nicht. Mit diesen besonderen Eigenschaften des gleichschenkligen Dreiecks lässt sich die Fläche mit wenigen Daten berechnen.

Schritte

Methode 1 von 2: Bestimmen der Fläche anhand der Längen jeder Seite

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 1

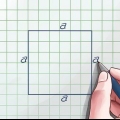
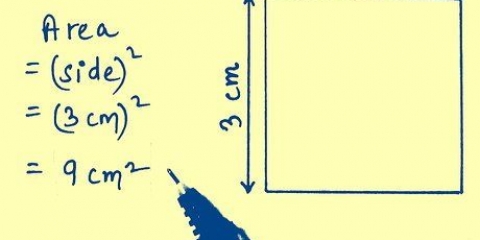
1. Nehmen Sie die Fläche eines Parallelogramms. Quadrate und Rechtecke sind Parallelogramme, wie jede vierseitige Form, bei der zwei Seitenpaare parallel zueinander sind. Alle Parallelogramme haben eine einfache Flächenformel: Fläche ist gleich Basis multipliziert mit Höhe, oder A = bh. Wenn Sie ein imaginäres Parallelogramm aufrecht auf einer horizontalen Fläche platzieren, ist die Basis die Länge der Seite, auf der sich die Figur befindet. Die Höhe ist der Abstand von der Basis zum höchsten Punkt (wie zu erwarten); d.h. der Abstand von der Basis zur gegenüberliegenden Seite. Messen Sie die Höhe immer im rechten Winkel (90 Grad) zur Basis.

Bei Quadraten und Rechtecken entspricht die Höhe der Länge einer vertikalen Seite, da diese Seiten im rechten Winkel zum Boden stehen.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 2

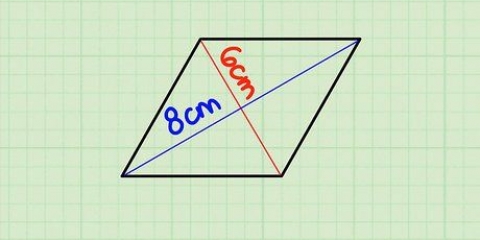
2. Vergleiche Dreiecke und Parallelogramme. Zwischen diesen beiden Formen besteht eine einfache Beziehung. Das Halbieren eines Parallelogramms entlang der Diagonalen teilt es in zwei gleiche Dreiecke. Ebenso können Sie zwei identische Dreiecke zu einem Parallelogramm zusammenfügen. Dies bedeutet, dass die Fläche eines Dreiecks geschrieben werden kann als A = bh, genau halb so groß wie ein entsprechendes Parallelogramm.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 3

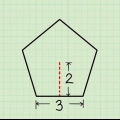
3. Finden Sie die Basis des gleichschenkligen Dreiecks. Jetzt haben Sie die Formel, aber was genau sind die "Basis" und die "Höhe" eines gleichschenkligen Dreiecks?? Die Basis ist der einfache Teil: Nimm einfach die dritte, ungleiche Seite des gleichschenkligen Dreiecks.

Wenn beispielsweise ein gleichschenkliges Dreieck Seiten von 5 cm, 5 cm und 6 cm hat, dann ist die Seite von 6 cm die Basis.

Wenn ein Dreieck drei gleiche Seiten hat (also gleichseitig ist), können Sie eine beliebige Seite als Basis wählen. Ein gleichseitiges Dreieck ist eine besondere Art von gleichschenkligen Dreiecken, aber Sie können seinen Flächeninhalt auf die gleiche Weise ermitteln.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 4

4. Zeichnen Sie eine Linie zwischen der Basis und dem gegenüberliegenden Scheitelpunkt. Stellen Sie sicher, dass die Linie die Basis im rechten Winkel berührt. Die Länge dieser Linie ist die Höhe des Dreiecks und wird daher mit bezeichnet h. Sobald Sie den Wert von erhalten haben h berechnet, können Sie die Fläche bestimmen.

In einem gleichschenkligen Dreieck berührt diese Linie die Basis immer genau in ihrer Mitte.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 5

5. Sehen Sie sich eine Hälfte des gleichschenkligen Dreiecks an. Beachten Sie, dass die Höhe das gleichschenklige Dreieck in zwei identische rechtwinklige Dreiecke teilt. Sehen Sie sich eine davon an und zeigen Sie auf die drei Seiten:

Eine der kurzen Seiten entspricht der Hälfte der Basis:

\frac{B}{2}

${frac{b}{2}}$ .

Die andere kurze Seite ist die Höhe h.

Die Hypotenuse (Hypotenuse) des rechtwinkligen Dreiecks ist eine der beiden gleichen Seiten des gleichschenkligen Dreiecks. Holen wir uns das S zu erwähnen.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 6

6.Verwenden Sie den Satz des Pythagoras. Wenn Sie zwei Seiten eines rechtwinkligen Dreiecks kennen und die dritte finden möchten, können Sie den Satz des Pythagoras verwenden: (Seite 1) + (Seite 2) = (Hypotenuse) Ersetzen Sie die Variablen, die wir in diesem Problem verwenden, und Sie erhalten

(\frac{B}{2})^{2} + h^{2} = S^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$ .

Sie haben wahrscheinlich den Satz des Pythagoras gelernt, wenn

ein 2 + B^{2} = C^{2}

$a^{2}+b^{2}=c^{2}$ . Das Schreiben als `Seiten` und `Hypotenuse` verhindert, dass Sie diese mit den Variablen des Dreiecks verwechseln.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 7

7. Lösen für h. Denken Sie daran, dass Sie die Flächenformel haben B und h verwendet, aber Sie kennen den Wert von nicht h weiß noch nicht. Schreibe die Formel um h lösen:

(\frac{B}{2})^{2} + h^{2} = S^{2}

$({frac{b}{2}})^{2}+h^{2}=s^{2}$

h 2 = S^{2} - (\frac{B}{2})^{2}

$h^{2}=s^{2}-({frac{b}{2}})^{2}$

h = \sqrt{(} S^{2} - (\frac{B}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$ .

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 8

8. Ersetzen Sie die Werte Ihres Dreiecks durch h Da Sie diese Formel jetzt kennen, können Sie sie für ein gleichschenkliges Dreieck verwenden, dessen Seiten Sie kennen. Geben Sie einfach die Länge der Basis für ein B und die Länge einer der gleichen Seiten für S, und danach berechnen h.

Sie haben zum Beispiel ein gleichschenkliges Dreieck mit den Seitenlängen 5 cm, 5 cm und 6 cm. B = 6 und S = 5.

Verwenden Sie diese Werte in Ihrer Formel:

h = \sqrt{(} S^{2} - (\frac{B}{2})^{2})

$h={sqrt(}s^{2}-({frac{b}{2}})^{2})$

h = \sqrt{(} 5^{2} - (\frac{6}{2})^{2})

$h={sqrt(}5^{2}-({frac{6}{2}})^{2})$

h = \sqrt{(} 25 - 3^{2})

$h={sqrt(}25-3^{2})$

h = \sqrt{(} 25 - 9)

$h={sqrt(}25-9)$

h = \sqrt{(} 16)

$h={sqrt(}16)$

h = 4

$h=4$ cm.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 9

9. Verwenden Sie die Basis- und Höhenwerte in der Flächenformel. Jetzt haben Sie, was Sie brauchen, um die Formel vom Anfang dieses Abschnitts zu verwenden: Fläche = ½bh. Ersetzen Sie die Werte für b und h in dieser Formel und berechnen Sie die Antwort. Vergiss nicht, deine Antwort in Quadrateinheiten zu schreiben.

Um mit dem Beispiel fortzufahren: Das 5-5-6-Dreieck hat eine Basis von 6 cm und eine Höhe von 4 cm.

A = bh
A = ½(6cm)(4cm)
A = 12cm.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 10

10. Versuchen Sie es mit einem schwierigeren Beispiel. Die meisten gleichschenkligen Dreiecke sind schwieriger zu bearbeiten als im vorherigen Beispiel. Höhe enthält oft eine Quadratwurzel, die nicht zu einer ganzen Zahl vereinfacht werden kann. Belassen Sie in diesem Fall die Höhe als Quadratwurzel im Einfachste Form stehen. Hier ist ein Beispiel:

Wie groß ist die Fläche eines Dreiecks mit den Seiten 8 cm, 8 cm und 4 cm?

Die unebene Seite beträgt 4 cm und die Basis B.

Die Höhe

h = \sqrt{8} 2 - (\frac{4}{2})^{2}

$h={sqrt{8^{2}-({frac{4}{2}})^{2}}}$

= \sqrt{64 - 4}

$={sqrt{64-4}}$

= \sqrt{60}

$={sqrt{60}}$

Vereinfachen Sie die Quadratwurzel durch Faktorisieren:

h = \sqrt{60} = \sqrt{4 * fünfzehn} = \sqrt{4} \sqrt{fünfzehn} = 2 \sqrt{fünfzehn} .

$h={sqrt{60}}={sqrt{4*15}}={sqrt{4}}{sqrt{15}}=2{sqrt{15}}$

Oberfläche

= \frac{1}{2} B h

$={frac{1}{2}}bh$

= \frac{1}{2} (4) (2 \sqrt{fünfzehn})

$={frac{1}{2}}(4)(2{sqrt{15}})$

= 4 \sqrt{fünfzehn}

$=4{sqrt{15}}$

Lassen Sie diese Antwort wie notiert oder verwenden Sie einen Taschenrechner für eine Dezimalschätzung (ca. 15,49 cm2).

Methode 2 von 2: Verwenden von Trigonometrie

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 11

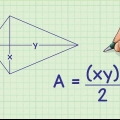
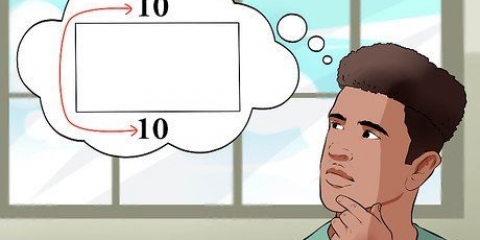
1. Beginnen Sie mit einer Seite und einer Ecke. Wenn Sie sich mit Trigonometrie auskennen, können Sie den Flächeninhalt eines gleichschenkligen Dreiecks auch dann ermitteln, wenn keine seiner Seitenlängen bekannt ist. Hier ist ein Beispielproblem, bei dem nur Folgendes bekannt ist:

Die Länge S der beiden gleichen Seiten beträgt 10 cm.
Der Winkel θ zwischen den beiden gleichen Seiten beträgt 120 Grad.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 12

2. Teilen Sie das gleichschenklige Dreieck in zwei rechtwinklige Dreiecke. Zeichnen Sie eine Linie vom Scheitelpunkt zwischen den beiden gleichen Seiten nach unten, die die Basis im rechten Winkel schneidet. Sie haben jetzt zwei gleiche rechtwinklige Dreiecke.

Diese Linie teilt θ perfekt in zwei Hälften. Jedes rechtwinklige Dreieck hat einen Winkel von ½θ, oder in diesem Fall (½)(120) = 60 Grad.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 13

3. Verwenden Sie Trigonometrie, um den Wert von zu bestimmen h. Nachdem Sie nun ein rechtwinkliges Dreieck haben, können Sie die trigonometrischen Funktionen (Sinus, Kosinus und Tangens) anwenden. In der Beispielaufgabe kennen Sie die Hypotenuse und möchten den Wert von h wissen, die Seite neben dem bekannten Winkel. Verwenden Sie die Tatsache, dass Kosinus = benachbart / Hypotenuse zu h lösen:

cos(θ/2) = h / s

cos(60º) = h / 10

h = 10cos(60º)

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 14

4. Bestimmen Sie den Wert der verbleibenden Seite. Es gibt eine noch unbekannte Seite des rechtwinkligen Dreiecks, die du x kann benennen. Lösen Sie dies mit der Definition Sinus = Gegenteil / Hypotenuse:

sin(θ/2) = x / s

sin(60º) = x / 10

x = 10sin(60º)

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 15

5. Verwenden Sie die Beziehung von x zur Basis des gleichschenkligen Dreiecks. Sie können jetzt auf das fragliche gleichschenklige Dreieck „herauszoomen“. Die Basis B dieses Winkels ist gleich 2x, da es in zwei Segmente mit jeweils einer Länge unterteilt war x.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 16

6. Verwenden Sie die Werte h und B in der Flächenformel für das Dreieck. Da Sie nun Basis und Höhe kennen, können Sie die Standardformel A = ½bh anwenden:

ein = \frac{1}{2} B h

$A={frac{1}{2}}bh$

= \frac{1}{2} (2 x) (10 C Ö S 60)

$={frac{1}{2}}(2x)(10cos60)$

= (10 S ich n 60) (10 C Ö S 60)

$=(10sin60)(10cos60)$

= 100 S ich n (60) C Ö S (60)

$=100sin(60)cos(60)$

Mit einem Taschenrechner (auf Grad eingestellt) erhalten Sie als Antwort etwa 43,3 cm2. Alternativ können Sie die Eigenschaften der Trigonometrie verwenden, um sie auf A = 50sin(1200) zu vereinfachen.

Finden Sie die Fläche eines gleichschenkligen Dreiecks Schritt 17

7. Schreiben Sie dies als universelle Formel um. Nachdem Sie nun wissen, wie Sie dies beheben können, können Sie die allgemeine Formel anwenden, ohne jedes Mal den gesamten Prozess durchlaufen zu müssen. Folgendes erhalten Sie, wenn Sie diesen Vorgang wiederholen, ohne bestimmte Werte zu verwenden (und mit den trigonometrischen Eigenschaften zu vereinfachen):

ein = \frac{1}{2} S^{2} S ich n θ

$A={frac{1}{2}}s^{2}sintheta$

s ist die Länge einer der beiden gleichen Seiten.

Θ ist der Winkel zwischen den beiden gleichen Seiten.

Tipps

Wenn Sie es mit einem gleichschenkligen rechtwinkligen Dreieck (zwei gleiche Seiten und einem Winkel von 90 Grad) zu tun haben, ist es viel einfacher, den Bereich zu finden. Wenn Sie eine der kurzen Seiten als Basis verwenden, ist die andere kurze Seite die Höhe. Nun kann die Formel A = ½ b * h auf ½s vereinfacht werden, wobei s die Länge einer kurzen Seite ist.
Quadratwurzeln haben zwei Lösungen, eine positive und eine negative, aber Sie können die negative in der Geometrie ignorieren. Sie können beispielsweise kein Dreieck mit einer `negativen Höhe` haben.
Einige trigonometrische Probleme geben Ihnen zunächst andere Informationen, wie die Länge der Basis und einen Winkel (und die Tatsache, dass das Dreieck gleichschenklig ist). Die Grundstrategie bleibt dieselbe: Das gleichschenklige Dreieck in rechtwinklige Dreiecke aufteilen und die Höhe mit trigonometrischen Funktionen berechnen.