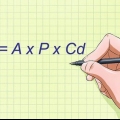Varianz berechnen: 8 Schritte (mit Bildern)

Schritte
Tipps

Durch die Berechnung der Varianz können Sie die Streuung einer Reihe von Werten messen – den Grad, in dem sich eine Reihe von Werten voneinander unterscheiden. Die Varianz ist eine der Komponenten der Wahrscheinlichkeitsverteilung und gibt an, inwieweit die Werte vom Mittelwert abweichen. Varianz wird oft zusammen mit der Standardabweichung (der Quadratwurzel der Varianz) verwendet. Wenn Sie wissen möchten, wie Sie die Varianz einer Reihe von Werten berechnen, führen Sie die folgenden Schritte aus.

Schritte

1. Schreiben Sie die Formel zur Berechnung der Varianz. Die Schätzung zur Berechnung einer zufälligen Schätzung der Populationsvarianz aus einer festen Stichprobe von n Beobachtungen ist die folgende Definition:(s) = Σ [(x_ich - x̅)]/n - 1. Die Formel zur Berechnung der Varianz in einer ganzen Grundgesamtheit ist dieselbe wie die vorherige, außer dass der Nenner nicht gleich n – 1, sondern n . ist. Solange Sie es mit einer endlichen Menge von Beobachtungen zu tun haben, ist es besser, die erste Formel zu verwenden. Hier ist eine Erklärung der Variablen der Formel:

s = Varianz
Σ = Summe, die Summe aller Terme in der Gleichung nach dem Summenzeichen.
x_ich = Die Beispielwerte.
x̅ = Der Mittelwert der Werte in der Reihe.
n = Die Stichprobengröße. Die Anzahl der Werte in der Reihe.

2. Berechnen Sie die Summe der Werte in der Reihe. Erstellen Sie zuerst eine Tabelle mit einer Spalte für die Werte, den Wert minus dem Mittelwert (x_ich - x̅) und dann das Quadrat dieser Terme [(x_ich - X))]. Nachdem Sie mit der Tabelle fertig sind und die erste Spalte ausgefüllt haben, addieren Sie alle Werte in der Reihe. Angenommen, Sie haben es mit folgender Zahlenfolge zu tun: 17, 15, 23, 7, 9, 13. Zusammengerechnet ergibt das: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Berechnen Sie den Durchschnitt. Dividiere die Summe der Zahlen in der Reihe durch die Anzahl der Elemente in der Reihe, um den Mittelwert zu berechnen. Also in diesem Fall die Summe 84 geteilt durch die Anzahl der Zahlen, 6. 84/6 = 14. schreiben "14" ganz unten in der Spalte als Durchschnitt.

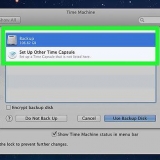
4. Subtrahiere den Mittelwert jedes Wertes der Reihe. Subtrahiere 14 von jedem Wert in der Reihe und fülle die dritte Spalte (den Stichprobenmittelwert) aus. Sie können Ihre Arbeit überprüfen, indem Sie prüfen, ob die Summe aller Ergebnisse Null ist. So berechnen Sie die Abweichung vom Mittelwert für jeden Wert in der Reihe:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Jedes Ergebnis quadrieren. Nachdem Sie die Abweichung vom Mittelwert berechnet haben, quadrieren Sie diese und schreiben Sie die Antwort in die vierte Spalte. Also alle Antworten sind positiv. So hat es geklappt:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Berechnen Sie die Summe der Quadrate. Füge die Ergebnisse zusammen. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Ersetzen Sie die Werte in der Gleichung. Tragen Sie die Werte in die Gleichung ein. Erinnere dich daran "n" repräsentiert die Anzahl der Elemente in der Sequenz.

s = 166/(6-1)

8. Lösen. Teile jetzt 166 durch 5. Das Ergebnis ist 33,2. Wenn Sie auch die Standardabweichung wissen möchten, finden Sie die Quadratwurzel von 33,2. √33,2 = 5,76. Jetzt können Sie beginnen, diese Daten in Bezug auf das große Ganze zu interpretieren. Normalerweise wird die Varianz zweier Reihen verglichen. Der niedrigste Wert bedeutet, dass in dieser Reihe die Varianz weniger groß ist.

Tipps

Da es schwierig sein kann, die Varianz zu interpretieren, wird dieser Wert normalerweise nur zu Beginn der Berechnung der Standardabweichung berechnet.