Kovarianz berechnen

Schritte
Warnungen

Kovarianz ist eine statistische Berechnung, um die Beziehung zwischen zwei Datensätzen transparenter zu machen. Nehmen wir zum Beispiel an, Anthropologen untersuchen die Größe und das Gewicht einer Bevölkerung innerhalb einer bestimmten Kultur. Für jede Person in der Studie können Größe und Gewicht mit einem Datenpaar (x, y) dargestellt werden. Diese Werte können in einer Standardformel zur Berechnung der Kovarianzrelation verwendet werden. In diesem Artikel werden zunächst die Berechnungen zur Bestimmung der Kovarianz eines Datensatzes erläutert. Als nächstes werden zwei weitere automatisierte Methoden zur Ermittlung des Ergebnisses diskutiert.

Schritte

Methode 1 von 4: Berechnung der Kovarianz von Hand mit der Standardformel

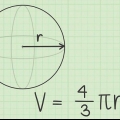
1. Lernen Sie die Standard-Kovarianzformel und ihre Teile. Die Standardformel zur Berechnung der Kovarianz ist

Σ (x ich - x_{durchschnittlich}) ({ja}_{ich} - {ja}_{durchschnittlich}) / (n - 1)

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})/(n-1)$ . Um diese Formel zu verwenden, müssen Sie die Bedeutung der Variablen und Symbole kennen:

$Σ$ $Sigma$ - Dieses Symbol ist der griechische Buchstabe `Sigma`. In mathematischen Funktionen bedeutet dies, eine Reihe von Folgendem hinzuzufügen:. In dieser Formel bedeutet das Σ-Zeichen, dass Sie die Werte im Zähler des Bruchs berechnen, dann alle addieren und dann die Summe durch den Nenner dividieren.
$x ich$ $x_{i}$ - Sie können diese Variable als `x sub i` lesen. Das tiefgestellte i steht für einen Zähler. Das bedeutet, dass Sie für jeden Wert von x in Ihrem Datensatz eine Berechnung durchführen werden.
$x ein v g$ $x_{{avg}}$ - Der `avg` gibt an, dass x(avg) der Mittelwert aller x Datenpunkte ist. Der Mittelwert wird manchmal als x mit einer kurzen horizontalen Linie darüber geschrieben. In diesem Stil lesen Sie die Variable als `x-bar`, aber es bedeutet immer noch den Mittelwert des Datensatzes.
$ja ich$ $y_{i}$ - Sie können diese Variable als `y sub i` lesen. Das tiefgestellte i ist der Zähler. Das bedeutet, dass Sie für jeden Wert von y in Ihrem Datensatz eine Berechnung durchführen werden.
$ja ein v g$ $j_{{avg}}$ - Der `avg` gibt an, dass y(avg) der Mittelwert aller x Datenpunkte ist. Der Mittelwert wird manchmal als y mit einer kurzen horizontalen Linie darüber geschrieben. In diesem Stil liest du die Variable als `y-bar`, aber es bedeutet immer noch den Mittelwert des Datensatzes.
$n$ $n$ - Diese Variable ist die Anzahl der Elemente in Ihrem Datensatz. Denken Sie daran, dass in einem Kovarianzproblem ein einzelnes `Element` sowohl aus einem x-Wert als auch einem y-Wert besteht. Der Wert `n` ist die Anzahl der Paare von Datenpunkten, nicht einzelne Zahlen.

2. Erstellen Sie Ihre Datentabelle. Bevor Sie beginnen, ist es sinnvoll, Ihre Daten zu sammeln. Erstellen Sie eine Tabelle mit fünf Spalten. Sie müssen jede Spalte wie folgt deklarieren:

x

$x$ - Füllen Sie diese Spalte mit den Werten der Punkte der x-Daten.

ja

$ja$ - Füllen Sie diese Spalte mit den Werten der y-Daten. Stellen Sie sicher, dass die y-Werte mit den entsprechenden x-Werten ausgerichtet sind. Bei einem Kovarianzproblem sind die Reihenfolge der Datenpunkte und die Kopplung von x und y wichtig.

(x ich - x_{durchschnittlich})

$(x_{i}-x_{{text{avg}}})$ - Lassen Sie diese Spalte am Anfang leer. Sie werden es mit Daten füllen, nachdem Sie die x-Daten gemittelt haben.

(ja ich - {ja}_{durchschnittlich})

$(y_{i}-y_{{text{avg}}})$ - Lassen Sie diese Spalte am Anfang leer. Sie werden es mit Daten füllen, nachdem Sie die y-Daten gemittelt haben.

Produkt

${text{Produkt}}$ - Lassen Sie auch die letzte Spalte leer. Dieser wird während der Bearbeitung des Auftrags ausgefüllt.

3. Berechnen Sie den Mittelwert der x Datenpunkte. Diese Beispieldatensammlung enthält 9 Zahlen. Um den Durchschnitt zu ermitteln, addieren Sie sie und teilen Sie die Summe durch 9. Dies ergibt das Ergebnis 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Wenn Sie dies durch 9 teilen, erhalten Sie den Mittelwert 4,89. Dies ist der Wert, den Sie als x(avg) für die nächsten Berechnungen verwenden werden.

4. Berechnen Sie den Mittelwert der y Datenpunkte. Diese y-Spalte muss auch aus 9 Datenpunkten bestehen, die mit den x-Datenpunkten übereinstimmen. Bestimmen Sie den Durchschnitt davon. Für diesen Beispieldatensatz wird es zu 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Teilen Sie diese Summe durch 9, um einen Durchschnitt von 5,44 . zu erhalten. Sie werden 5,44 als Wert von y(avg) für die kommenden Berechnungen verwenden.

5. Berechnen Sie die Werte (xich-xdurchschnittlich){displaystyle (x_{i}-x_{text{avg}})} $(x_{i}-x_{{text{avg}}})$ . Berechnen Sie für jedes Element in der x-Spalte die Differenz zwischen dieser Zahl und dem Mittelwert. Für dieses Beispielproblem bedeutet dies, dass von jedem x-Wert 4,89 abgezogen werden. Wenn der ursprüngliche Datenpunkt kleiner als der Mittelwert ist, ist Ihr Ergebnis negativ. Wenn der ursprüngliche Datenpunkt größer als der Mittelwert ist, ist das Ergebnis positiv. Achte darauf, welche Werte negativ sind.

Der erste Datenpunkt in der x-Spalte ist beispielsweise 1. Der in die erste Zeile der Spalte einzugebende Wert

(x ich - x_{durchschnittlich})

$(x_{i}-x_{{text{avg}}})$ ist: 1 – 4,89 = -3,89.

Wiederholen Sie diesen Vorgang für jeden Datenpunkt. Die zweite Zeile wird also: 3 - 4,89 = -1.89. Die dritte Zeile wird: 2 - 4,89 = -2,89. Setzen Sie diesen Vorgang für alle Datenpunkte fort. Die neun Zahlen in dieser Spalte werden zu: -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7,11, -2,89, -0,89.

6. Berechnen Sie die Werte (jaich-jadurchschnittlich){displaystyle (y_{i}-y_{text{avg}})} $(y_{i}-y_{{text{avg}}})$ . In dieser Spalte werden Sie ähnliche Subtraktionen durchführen, indem Sie die y-Datenpunkte und den y-Mittelwert verwenden. Wenn der ursprüngliche Datenpunkt kleiner als der Mittelwert ist, ist das Ergebnis negativ. Wenn der ursprüngliche Datenpunkt größer als der Mittelwert ist, ist Ihr Ergebnis positiv. Achte darauf, welche Werte negativ sind.

Für die erste Zeile lautet Ihre Berechnung also: 8 -5,44, = 2,56.

Die zweite Zeile wird: 6 – 5,44 = 0,56.

Ziehe die Werte weiter bis zum Ende der Datenliste ab. Wenn Sie fertig sind, sollten Sie die folgenden neun Werte in dieser Spalte haben: 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44 , 1,56, 1,56.

7. Berechnen Sie die Produkte für jede Datenzeile. Sie füllen die Zeilen der letzten Spalte aus, indem Sie die Zahlen multiplizieren, die Sie in den beiden vorherigen Spalten von berechnet haben

(x ich - x_{durchschnittlich})

$(x_{i}-x_{{text{avg}}})$ und

(ja ich - {ja}_{durchschnittlich})

$(y_{i}-y_{{text{avg}}})$ . Arbeiten Sie sich Zeile für Zeile vor und multiplizieren Sie die beiden Zahlen mit den entsprechenden Datenpunkten. Achten Sie auf negative Werte auf dem Weg.

In der ersten Zeile dieser Beispieldaten steht das

(x ich - x_{durchschnittlich})

$(x_{i}-x_{{text{avg}}})$ Sie haben -3,89 berechnet, und die

(ja ich - {ja}_{durchschnittlich})

$(y_{i}-y_{{text{avg}}})$ Wert 2,56. Das Produkt dieser beiden Zahlen ist: -3,89 x 2,56 = -9,96.

Für die zweite Reihe multiplizieren Sie die beiden Zahlen: -1,88 x 0,56 = -1,06.

Multiplizieren Sie Zeile für Zeile bis zum Ende des Datensatzes. Wenn Sie fertig sind, sollten die neun Werte in dieser Spalte lauten: -9,96, -1,06, -10,29, -0,16, -7,59, -5,15, -24,46 , -4,51, -1,39.

8. Finden Sie die Summe der Werte in der letzten Spalte. Hier kommt das Σ-Symbol ins Spiel. Nachdem Sie alle bisherigen Berechnungen durchgeführt haben, addieren Sie die Ergebnisse zusammen. Für diesen Beispieldatensatz sollten Sie nun in der letzten Spalte neun Werte haben. Addiere diese neun Zahlen zusammen. Achte genau darauf, ob eine Zahl positiv oder negativ ist.

Die Summe dieses Beispieldatensatzes sollte -64,57 . ergeben. Schreiben Sie diese Summe in das Feld am unteren Rand der Spalte. Dies ist der Wert des Zählers der Standardkovarianzformel.

9. Berechnen Sie den Nenner der Kovarianzformel. Der Zähler der Standard-Kovarianzformel ist der gerade berechnete Wert. Der Nenner wird durch (n-1) dargestellt und ist eins weniger als die Anzahl der Datenpaare in Ihrem Datensatz.

In diesem Beispielproblem gibt es neun Datenpaare, also ist n 9. Daher ist der Wert von (n-1) gleich 8.

10. Dividiere den Zähler durch den Nenner. Der letzte Schritt bei der Berechnung der Kovarianz besteht darin, den Zähler zu dividieren,

Σ (x ich - x_{durchschnittlich}) ({ja}_{ich} - {ja}_{durchschnittlich})

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})$ nach dem Nenner,

(n - 1)

$(n-1)$ . Der Quotient ist die Kovarianz Ihrer Daten.

Für diesen Beispieldatensatz lautet diese Berechnung: -64,57/8 = -8,07.

Methode 2 von 4: Berechnen Sie die Kovarianz mit einem Excel-Arbeitsblatt

1. Beachten Sie die sich wiederholenden Berechnungen. Kovarianz ist eine Berechnung, die Sie einige Male von Hand durchführen müssen, damit Sie die Bedeutung des Ergebnisses verstehen. Wenn Sie jedoch routinemäßig die Kovarianz zur Interpretation von Daten verwenden, benötigen Sie einen schnelleren und automatisierten Weg, um die Ergebnisse zu erhalten. Sie haben vielleicht schon bemerkt, dass bei unserem relativ kleinen Datensatz von nur neun Datenpaaren die Berechnungen aus zwei Mittelwerten, achtzehn separaten Subtraktionen, neun Multiplikationen, einer Addition und schließlich einer weiteren Division bestanden. Das sind 31 relativ kleine Berechnungen, um die Lösung zu finden. Unterwegs laufen Sie Gefahr, negative Vorzeichen zu übersehen oder die Ergebnisse falsch zu kopieren, wodurch die Antwort falsch ist.

2. Erstellen Sie ein Arbeitsblatt zur Berechnung der Kovarianz. Wenn Sie mit Excel (oder einem anderen Berechnungsprogramm) vertraut sind, können Sie ganz einfach eine Tabelle zur Bestimmung der Kovarianz erstellen. Beschriften Sie die Überschriften der fünf Spalten wie in den manuellen Berechnungen: x, y, (x(i)-x(avg)), (y(i)-y(avg)) und Product.

Um die Benennung zu vereinfachen, benennen Sie die dritte Spalte etwa "x-Differenz" und die vierte Spalte "y-Differenz", solange Sie sich an die Bedeutung der Daten erinnern.

Wenn die Tabelle in der oberen linken Ecke des Arbeitsblatts beginnt, wird Zelle A1 mit x beschriftet, während die anderen Beschriftungen mit Zelle E1 fortfahren.

3. Füllen Sie die Datenpunkte aus. Geben Sie die Datenwerte in die beiden Spalten x und y ein. Denken Sie daran, dass die Reihenfolge der Datenpunkte wichtig ist, daher müssen Sie jedes y mit dem entsprechenden Wert von x . abgleichen.

Die x-Werte beginnen in Zelle A2 und werden bis zur Anzahl der benötigten Datenpunkte fortgesetzt.

Die y-Werte beginnen in Zelle B2 und werden bis zur Anzahl der benötigten Datenpunkte fortgesetzt.

4. Bestimmen Sie die Mittelwerte der x- und y-Werte. Excel berechnet die Durchschnittswerte für Sie sehr schnell. Geben Sie in die erste leere Zelle unter jeder Datenspalte die Formel ein = MITTELWERT(A2: A___). Füllen Sie die Lücke mit der Nummer der Zelle, die Ihrem letzten Datenpunkt entspricht.

Wenn Sie beispielsweise 100 Datenpunkte haben, werden die Zellen A2 bis A101 gefüllt. Geben Sie in die Zelle Folgendes ein: = AVERAGE(A2:A101).

Geben Sie für die y-Daten die Formel ein = AVERAGE(B2:B101).

Denken Sie daran, dass eine Formel in Excel mit einem `=`-Zeichen beginnt.

5. Geben Sie die Formel für die Spalte ein (x(i)-x(avg)). Geben Sie in Zelle C2 die Formel zur Berechnung der ersten Subtraktion ein. Diese Formel wird zu: =A2-___. Füllen Sie den leeren Raum mit der Zellenadresse, die den Durchschnitt der x-Daten enthält.

Zum Beispiel werden die 100 Datenpunkte in Zelle A103 gemittelt, also lautet Ihre Formel: =A2-A103.

6. Wiederholen Sie die Formel für die Datenpunkte (y(i)-y(avg)). Nach dem gleichen Beispiel befindet es sich in Zelle D2. Die Formel wird: =B2-B103.

7. Geben Sie die Formel für die Spalte "Produkt" ein. In die fünfte Spalte müssen Sie in Zelle E2 die Formel zur Berechnung des Produkts der beiden vorhergehenden Zellen eingeben. Daraus wird dann: =C2*D2.

8. Kopieren Sie die Formeln, um die Tabelle auszufüllen. Bisher haben Sie nur die ersten Datenpunkte in Zeile 2 programmiert. Markieren Sie mit der Maus die Zellen C2, D2 und E2. Setzen Sie Ihren Cursor auf das kleine Kästchen in der unteren rechten Ecke, bis ein Pluszeichen erscheint. Klicken und halten Sie die Maustaste und ziehen Sie die Maus nach unten, um die Auswahl zu erweitern und die gesamte Datentabelle auszufüllen. Dieser Schritt kopiert automatisch die drei Formeln aus den Zellen C2, D2 und E2 in die gesamte Tabelle. Die Tabelle sollte automatisch mit allen Berechnungen gefüllt werden.

9. Programmieren Sie die Summe der letzten Spalte. Sie benötigen die Summe der Artikel in der Spalte `Produkt`. Geben Sie in die leere Zelle direkt unter dem letzten Datenpunkt in dieser Spalte die Formel ein: =SUM(E2:E___). Füllen Sie die Lücke mit der Zellenadresse des letzten Datenpunkts.

Im Beispiel mit 100 Datenpunkten geht diese Formel in Zelle E103. Typ: =SUMME(E2:E102).

10. Bestimmen Sie die Kovarianz. Sie können auch Excel die endgültige Berechnung für Sie übernehmen lassen. Die letzte Berechnung in Zelle E103 in unserem Beispiel stellt den Zähler der Kovarianzformel dar. Geben Sie direkt unter dieser Zelle die Formel ein: =E103/___. Füllen Sie die Lücke mit der Anzahl der Datenpunkte, die Sie haben. In unserem Beispiel sind das 100. Das Ergebnis ist die Kovarianz Ihrer Daten.

Methode 3 von 4: Online-Kovarianzrechner verwenden

1. Online nach Kovarianzrechnern suchen. Diverse Schulen, Firmen oder andere Quellen haben Websites, die die Kovarianzwerte ganz einfach für dich berechnen. Verwenden Sie den Suchbegriff `Kovarianzrechner` in einer Suchmaschine.

2. Geben Sie ihre Details ein. Bitte lesen Sie die Anweisungen auf der Website sorgfältig durch, um sicherzustellen, dass Sie die Informationen richtig eingeben. Es ist wichtig, dass Ihre Datenpaare in Ordnung sind, da sonst das generierte Ergebnis eine falsche Kovarianz ist. Websites haben unterschiedliche Dateneingabestile.

Auf der Internetseite http://nrechner.com/statistics/covariance-calculator.htm, gibt es zum Beispiel ein horizontales Kästchen zum Eingeben der x-Werte und ein zweites horizontales Kästchen zum Eingeben der y-Werte. Sie müssen Ihre Daten durch Kommas getrennt eingeben. Der zuvor in diesem Artikel berechnete x-Datensatz sollte dann als 1,3,2,5,8,7,12,2,4 . eingegeben werden. Die y-Daten als 8,6,9,4,3,3,2,7,7.

Auf einer anderen Seite, https://www.der Taschenrechner.co/mathe/Kovarianz-Rechner-705.html, Sie werden aufgefordert, die x-Daten in das erste Feld einzugeben. Die Daten werden vertikal eingegeben, mit einem Element pro Zeile. Daher sieht der Eintrag auf dieser Seite wie folgt aus:

3. Berechnen Sie Ihre Ergebnisse. Das Schöne an diesen Online-Berechnungen ist, dass Sie nach der Eingabe der Daten in der Regel nur noch auf die Schaltfläche `Berechnen` klicken müssen, woraufhin die Ergebnisse automatisch erscheinen. Die meisten Websites bieten Ihnen die Zwischenberechnungen von x(avg), y(avg) und n.

Methode 4 von 4: Interpretieren der Ergebnisse der Kovarianz

1. Suchen Sie nach einer positiven oder negativen Beziehung. Die Kovarianz ist eine einzelne statistische Zahl, die die Beziehung zwischen einem Datensatz und einem anderen anzeigt. Im eingangs erwähnten Beispiel werden Körpergröße und Gewicht gemessen. Sie würden erwarten, dass mit zunehmendem Wachstum auch ihr Gewicht zunimmt, was zu einer positiven Kovarianzansicht führt. Ein weiteres Beispiel: Angenommen, es werden Daten gesammelt, die angeben, wie viele Stunden eine Person Golf gespielt hat und welche Punktzahl sie erreicht. In diesem Fall erwarten Sie eine negative Kovarianz, d. h. mit steigender Trainingsstundenzahl sinkt der Golf-Score. (Beim Golf ist eine niedrigere Punktzahl besser).

Betrachten Sie den oben berechneten Beispieldatensatz. Die resultierende Kovarianz beträgt -8,07. Das Minuszeichen bedeutet, dass mit steigenden x-Werten die y-Werte tendenziell abnehmen. Sie können sehen, dass dies wahr ist, wenn Sie sich einige der Werte ansehen. Beispielsweise entsprechen die x-Werte von 1 und 2 den y-Werten von 7, 8 und 9. Die x-Werte von 8 und 12 sind mit den y-Werten von 3 bzw. 2 verknüpft.

2. Interpretieren Sie die Größe der Kovarianz. Wenn die Zahl des Kovarianz-Scores groß ist, entweder eine große positive Zahl oder eine große negative Zahl, können Sie dies als zwei Datenelemente interpretieren, die entweder positiv oder negativ stark miteinander verbunden sind.

Die Kovarianz -8,07 des Beispieldatensatzes ist ziemlich groß. Beachten Sie, dass die Daten von 1 bis 12 reichen. 8 ist also eine ziemlich große Zahl. Dies deutet auf eine ziemlich starke Beziehung zwischen den Datensätzen x und y hin.

3. Verstehe das Fehlen einer Beziehung. Wenn Ihr Ergebnis eine Kovarianz gleich oder sehr nahe 0 ist, können Sie daraus schließen, dass die Datenpunkte keine Beziehung haben. Das heißt, eine Erhöhung des einen Wertes kann, muss aber nicht zu einer Erhöhung des anderen führen. Die beiden Begriffe sind fast willkürlich verknüpft.

Angenommen, Sie beziehen Schuhgrößen auf Prüfungsnoten. Da es so viele Faktoren gibt, die die Prüfungsnoten eines Schülers beeinflussen, ist ein Kovarianzwert nahe 0 zu erwarten. Dies deutet darauf hin, dass es fast keinen Zusammenhang zwischen den beiden Werten gibt.

4. Betrachten Sie die Beziehung grafisch. Um die Kovarianz visuell zu verstehen, können Sie Ihre Datenpunkte in einem XY-Diagramm darstellen. Wenn Sie das tun, sollten Sie ziemlich leicht erkennen, dass die Punkte, obwohl sie nicht genau auf einer geraden Linie liegen, dazu neigen, sich einem Cluster in einer diagonalen Linie von links oben nach rechts unten zu nähern. Dies ist die Beschreibung einer negativen Kovarianz. Sie sehen auch, dass der Wert der Kovarianz -8,07 . beträgt. Dies ist eine ziemlich große Zahl im Vergleich zu den Datenpunkten. Die hohe Zahl deutet darauf hin, dass die Kovarianz ziemlich stark ist, was aus der linearen Form der Datenpunkte abgeleitet werden kann.

Um dies noch einmal zu überprüfen, lies wikiHow-Artikel über das Zeichnen von Punkten in einem Koordinatensystem.

Warnungen

Kovarianz hat in der Statistik nur begrenzte Anwendungsmöglichkeiten. Es ist oft ein Schritt zur Berechnung von Korrelationskoeffizienten oder anderen Konzepten. Seien Sie vorsichtig bei zu fetten Interpretationen basierend auf einem Kovarianzwert.