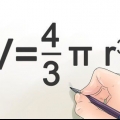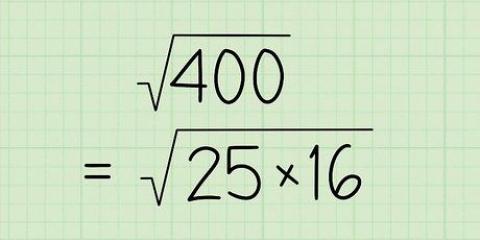Angenommen, Ihnen wird gesagt, dass es eine Kugel mit einem Radius von 10 cm . gibt. Finden Sie das Volumen wie folgt: 





Bestimmen Sie als Beispiel für diese Berechnung das Volumen einer Kugel mit einem Durchmesser von 10 cm. 















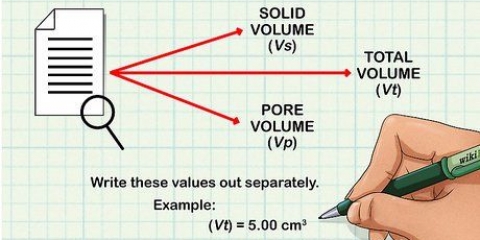
Gießen Sie genug Wasser in die Tasse, um die Zwiebel zu bedecken. Beachten Sie die Lautstärke. Gießen Sie die Zwiebel ins Wasser. Beachten Sie, dass der Wasserstand steigt. Beachten Sie den neuen Band. Subtrahiere den ersten Band vom zweiten. Das Ergebnis ist das Volumen der Kugel. Angenommen, Ihr Wasserstand steigt von 100 ml auf 625 ml, wenn Sie die Glühbirne eintauchen. Das Volumen beträgt also 525 ml. Beachten Sie, dass 1 ml = 1 cm. 

Alle Beispiele im vorherigen Abschnitt ergaben Volumina gemessen in Kubikzentimetern. Die angegebene Dichtetabelle gibt jedoch Dichten basierend auf Kubikmetern an. Weil ein Meter 100 Zentimeter hat, hat ein Kubikmeter 10 Kubikzentimeter. Teilen Sie die angegebenen Dichten durch 10, um die Dichte in Einheiten von kg/cm zu erhalten (einfach durch Verschieben des Dezimalkommas um sechs Stellen nach links). Für die vier zuvor aufgeführten Materialien sind die umgerechneten Dichten wie folgt: Aluminium = 2700 kg/m = 0,0027 kg/cm Butter = 870 kg/m3 = 0,00087 kg/cm Blei = 11.350 kg/m = 0,01135 kg/cm² Pressholz = 190 kg/m = 0,00019 kg/cm 
Mit den vier zuvor genannten Materialien Aluminium, Butter, Blei und Pressholz bestimmen Sie die Masse einer Kugel mit einem Volumen von 500 cm. 






Sie haben auch gelesen, dass die Kugel aus Messing ist. Sie müssen die Messingdichte in Ihren Binas oder aus einer anderen Quelle nachschlagen. Auf der Website EngineeringToolbox.com können Sie nachschlagen, dass die Dichte von Messing 8480 kg/m² beträgt. Da der Durchmesser der Kugel in Metern angegeben wird, wird ihr Volumen in Kubikmetern berechnet, sodass Sie die Dichte nicht umrechnen müssen. 









Berechnen sie die masse einer kugel
Einfach gesagt, eine Kugel ist eine solide runde Kugel. Um die Masse einer Kugel zu berechnen, müssen Sie die Größe (Volumen) der Kugel und ihre Dichte kennen. Sie können das Volumen anhand des Radius, Umfangs oder Durchmessers der Kugel berechnen. Sie können die Kugel auch in Wasser tauchen, um das Volumen durch Wasserverdrängung zu ermitteln. Wenn Sie das Volumen kennen, können Sie es mit der Dichte multiplizieren, um die Masse zu finden.
Schritte
Teil 1 von 3: Das Volumen einer Kugel bestimmen

1. Verwenden Sie die Formel für das Volumen einer Kugel. Eine Kugel ist ein kreisförmiger Körper in drei Dimensionen. Die Hauptformel für das Volumen einer Kugel lautet:

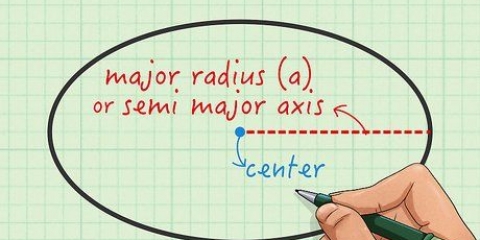
2. Bestimme das Volumen einer Kugel, wenn du ihren Radius kennst. Der Radius einer Kugel ist das Maß vom Mittelpunkt der Kugel zum äußeren Rand. Wenn Sie ein Problem bei der Berechnung des Volumens haben, ist wahrscheinlich der Radius angegeben. Andernfalls kann es schwierig sein, den Radius zu messen, da Sie den Mittelpunkt eines festen Objekts nicht genau bestimmen können.





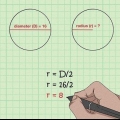
3. Bestimmen Sie das Volumen, wenn der Durchmesser angegeben ist. Eine andere Möglichkeit ist, dass für eine bestimmte Situation der Durchmesser einer Kugel gegeben ist. Der Durchmesser ist gleich dem doppelten Radius. Tatsächlich ist der Durchmesser der Abstand von einer Kante der Kugel durch das Zentrum zur anderen Kante. Um das Volumen aus dem Durchmesser (d) zu berechnen, überarbeiten Sie die Formel wie folgt:







4. Überarbeiten Sie die Formel, wenn Sie den Umfang kennen. Der Umfang einer Kugel ist wahrscheinlich am einfachsten direkt zu messen. Sie können ein Maßband verwenden, es vorsichtig um die breiteste Stelle der Zwiebel wickeln und die Messung durchführen. Vielleicht ist der Umfang in einer Aussage angegeben. Um das Volumen beginnend mit dem Umfang (C) zu ermitteln, überarbeiten Sie die Formel wie folgt:





5. Berechnen Sie das Volumen, wenn Sie den Umfang kennen. Angenommen, Sie erhalten eine Kugel und messen den Umfang bei 32 cm. Finden Sie das Volumen wie folgt:





6. Messen Sie das Volumen durch Wasserverdrängung. Eine letzte praktische Methode zur Volumenmessung ist das Eintauchen der Glühbirne in Wasser. Sie müssen einen Becher haben, der groß genug ist, um die Glühbirne mit genauen Volumenmarkierungen einzutauchen.
Teil 2 von 3: Masse aus Volumen berechnen

1. Bestimmen Sie die Dichte. Um die Masse aus dem Volumen zu berechnen, müssen Sie die Dichte des Objekts kennen. Unterschiedliche Materialien haben unterschiedliche Dichten. Betrachten Sie zum Beispiel eine Kugel aus Styropor und vergleichen Sie ihr Gewicht mit einer Kugel derselben Größe aus Eisen. Eisen hat eine viel größere Dichte und wird daher eine größere Masse haben.
- Sie können die Dichte vieler fester Materialien online, in Lehrbüchern oder in einem Binas nachschlagen.
- Hier sind zum Beispiel die aufgezeichneten Dichten einiger fester Materialien:
- Aluminium = 2700 kg/m²
- Butter = 870 kg/m²
- Blei = 11.350 kg/m²
- Pressholz = 190 kg/m²

2. Konvertieren Sie die Einheiten nach Bedarf. Die Einheiten, die Sie bei der Berechnung des Volumens verwenden, müssen mit den Volumeneinheiten der gemessenen Dichte übereinstimmen. Wenn nicht, müssen Sie sie konvertieren.

3. Multiplizieren Sie das Volumen mit der Dichte, um die Masse zu finden. Die Formel für die Dichte lautet  , wie du dich vielleicht erinnerst. Wenn Sie dies neu anordnen, um die Masse zu finden, wird die Gleichung
, wie du dich vielleicht erinnerst. Wenn Sie dies neu anordnen, um die Masse zu finden, wird die Gleichung  .
.
 , wie du dich vielleicht erinnerst. Wenn Sie dies neu anordnen, um die Masse zu finden, wird die Gleichung
, wie du dich vielleicht erinnerst. Wenn Sie dies neu anordnen, um die Masse zu finden, wird die Gleichung  .
.



Teil 3 von 3: Lösen eines Beispielproblems

1. Lesen Sie die Aufgabenstellung sorgfältig durch. Lesen Sie bei der Beantwortung von Problemen mit Massenberechnungen die gesamte Erklärung sorgfältig durch. Beim Lesen kann es hilfreich sein, den Eintrag hervorzuheben. Lesen Sie das gesamte Problem sorgfältig durch, um zu sehen, was Sie lösen müssen. Betrachten Sie beispielsweise das folgende Problem:
- Eine große Kugel aus massivem Messing hat einen Durchmesser von 1,2 m. Bestimme die Masse der Kugel.

2. Organisieren Sie die bekannten und unbekannten Daten. Wenn Sie die Aussage aufmerksam lesen, können Sie feststellen, dass der Durchmesser angegeben ist, also verwenden Sie die modifizierte Formel:


3. Berechnen Sie das Volumen. Um das Volumen zu berechnen, geben Sie die entsprechende Formel ein, geben Sie die Ihnen bekannten Daten ein und führen Sie die Berechnungen wie folgt durch:






4. Verwenden Sie die Dichte, um die Masse zu berechnen. Denken, dass  . Geben Sie die Ihnen bekannten Werte in die Formel ein, um die Masse zu ermitteln:
. Geben Sie die Ihnen bekannten Werte in die Formel ein, um die Masse zu ermitteln:
 . Geben Sie die Ihnen bekannten Werte in die Formel ein, um die Masse zu ermitteln:
. Geben Sie die Ihnen bekannten Werte in die Formel ein, um die Masse zu ermitteln:


Tipps
- Diese Erklärung geht davon aus, dass die Dichte der Kugel überall gleich ist. Dies wird in den meisten mathematischen und physikalischen Problemen vorausgesetzt. Es ist jedoch möglich, dass der Kern einer Kugel aus einem anderen Material besteht als die Oberfläche.
"Berechnen sie die masse einer kugel"
Оцените, пожалуйста статью