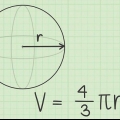
bol: wobei r der Radius der Kugel ist.
wobei r der Radius der Kugel ist. Kegel: wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist.
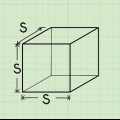
wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist. Würfel:  wobei s die Länge einer Seite ist.
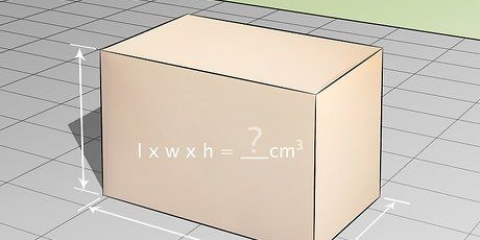
wobei s die Länge einer Seite ist. Rechteckiges Prisma:  wobei l die Seitenlänge einer rechteckigen Fläche ist, w die Breite einer rechteckigen Fläche und h die Höhe des Prismas ist.
wobei l die Seitenlänge einer rechteckigen Fläche ist, w die Breite einer rechteckigen Fläche und h die Höhe des Prismas ist. Zylinder:  wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist.
wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist. Pyramide:  wobei B die Grundfläche der Pyramide und h die Höhe der Pyramide ist.
wobei B die Grundfläche der Pyramide und h die Höhe der Pyramide ist. 
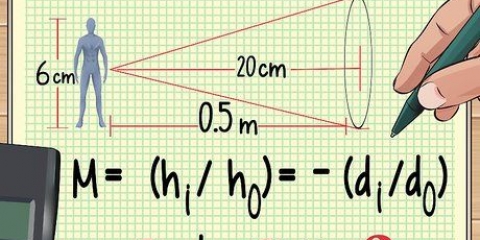
Der Radius eines Kreises ist der halbe Durchmesser. Messen Sie den Durchmesser mit einem Lineal durch die Mitte des Kreises und lesen Sie den Messwert ab. Berechnen Sie den Radius, indem Sie den Durchmesser durch zwei teilen. Die Bestimmung des Radius einer Kugel erfordert etwas mehr Aufwand, kann aber auf verschiedene Weise erfolgen, wie in gezeigt Dieser Beitrag. Die Länge, Breite und Höhe von Objekten kann mit einem Lineal gemessen werden, das von einem Ende eines Objekts zum anderen misst. 
Vergiss nicht, deine Antwort in Kubikeinheiten anzugeben. Unabhängig davon, ob Sie Metriken oder SIs verwenden, die Volumeneinheit ist immer Kubik. Fügen Sie immer Einheiten am Ende Ihrer Berechnung hinzu. 

Achten Sie beim Messen des anfänglichen Wasservolumens auf den Flüssigkeitsstand auf Augenhöhe und notieren Sie den Messwert auf der Unterseite des Meniskus. Der Meniskus ist die Kurve, die Wasser macht, wenn es mit einer Oberfläche in Kontakt kommt. 
Wenn Sie beim Einlegen des Gegenstands in den Becher Wasser verschüttet haben, versuchen Sie es erneut mit einem größeren Messbecher oder verwenden Sie weniger Wasser. 
Angenommen, Sie haben mit 35 ml Wasser begonnen und mit 65 ml Wasser geendet; das Volumen Ihres Objekts beträgt dann 65 – 35 = 30 ml oder 30 cm 


Berechnen Sie zum Beispiel die Dichte  eines Stoffes mit einem Volumen von 8 cm und einer Masse von 24 g.
eines Stoffes mit einem Volumen von 8 cm und einer Masse von 24 g. 
Volumen und dichte berechnen
Das Volumen ist der Raum, den ein Objekt einnimmt, während die Dichte die Masse des Objekts pro Volumeneinheit ist. Sie müssen zuerst das Volumen eines Objekts kennen, bevor Sie seine Dichte berechnen können. Sie können das Volumen für regelmäßige Objekte mit einer einfachen Formel berechnen, die durch die Form des Objekts bestimmt wird. Gebräuchliche Einheiten für Volumen sind Kubikzentimeter (cm) und Kubikmeter (m). Nachdem Sie das Volumen berechnet haben, wird die Dichte mit einer einfachen Rechnung bestimmt. Üblicherweise verwendete Einheiten für die Dichte sind Gramm pro Kubikzentimeter (g/cm) oder Gramm pro Milliliter (g/ml).
Schritte
Teil 1 von 3: Das Volumen eines regelmäßigen Objekts berechnen

1. Bestimmen Sie die Form des Objekts. Wenn Sie die Form eines Objekts kennen, können Sie die richtige Formel bestimmen und die erforderlichen Berechnungen für das Volumen durchführen.
- EIN Kugel ist ein perfekt rundes dreidimensionales Objekt, bei dem jeder Punkt auf seiner Oberfläche gleich weit vom Zentrum entfernt ist. Mit anderen Worten, eine Kugel ist ein kugelförmiges Objekt.
- EIN Kegel ist ein dreidimensionales Objekt mit kreisförmiger Grundfläche und einem Punkt. Man kann sich das auch so vorstellen, dass ein Kegel eine besondere Art von Pyramide mit kreisförmiger Grundfläche ist.
- EIN Würfel ist eine dreidimensionale Form mit sechs identischen quadratischen Flächen.
- EIN parallelepiped, auch rechteckiges Prisma genannt, sieht aus wie ein Würfel, da es eine dreidimensionale Form mit sechs Seiten ist, aber in diesem Fall sind die Seiten rechteckig statt quadratisch.
- EIN Zylinder ist eine dreidimensionale Form mit zwei identischen flachen Kreisen und einer einzigen gekrümmten flachen Oberfläche, die beide Kreise verbindet.
- EIN Pyramide ist eine dreidimensionale Form mit einem Polygon als Basis und schrägen Seiten, die sich in einem Punkt (der Spitze der Pyramide) treffen.Eine regelmäßige Pyramide ist eine Pyramide mit einem regelmäßigen Vieleck als Basis der Pyramide, was bedeutet, dass alle Seiten des Vielecks gleich lang und alle Winkel gleich groß sind.
- Wenn Ihr Objekt eine unregelmäßige Form hat, können Sie das Volumen mit der Verschiebungsmethode bestimmen.

2. Wählen Sie die richtige Gleichung für die Volumenberechnung. Jede Form hat ihre eigene Formel, um zu berechnen, wie viel dreidimensionalen Raum sie einnimmt. Nachfolgend finden Sie die Formeln für die zuvor genannten Objekte. Lesen Sie mehr darüber Berechnung des Volumens für detailliertere Beispiele und Bilder dieser Formeln.
 wobei r der Radius der Kugel ist.
wobei r der Radius der Kugel ist. wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist.
wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist. wobei s die Länge einer Seite ist.
wobei s die Länge einer Seite ist. wobei l die Seitenlänge einer rechteckigen Fläche ist, w die Breite einer rechteckigen Fläche und h die Höhe des Prismas ist.
wobei l die Seitenlänge einer rechteckigen Fläche ist, w die Breite einer rechteckigen Fläche und h die Höhe des Prismas ist. wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist.
wobei r der Radius der kreisförmigen Grundfläche und h die Höhe des Kegels ist. wobei B die Grundfläche der Pyramide und h die Höhe der Pyramide ist.
wobei B die Grundfläche der Pyramide und h die Höhe der Pyramide ist.
3. Nehmen Sie die erforderlichen Messungen vor. Die von Ihnen benötigten Maße werden durch die Form des Objekts bestimmt. Für die meisten Objekte benötigen Sie die Höhe, aber der Radius reicht aus, wenn die Form kreisförmig ist oder die Länge und Breite von Objekten mit rechteckigen Flächen.

4. Berechnen Sie das Volumen. Nachdem Sie nun die Form bestimmt, die zu verwendende Formel kennen und die erforderlichen Messungen vorgenommen haben, können Sie das Volumen berechnen. Geben Sie Ihre Messwerte ein und führen Sie die erforderlichen Berechnungen durch. Das Endprodukt ist das Volumen Ihres Objekts.
Teil 2 von 3: Berechnen Sie das Volumen eines unregelmäßigen Objekts

1. Berechnen Sie das Volumen des Objekts mit der Verschiebung. Bei unregelmäßig geformten Objekten kann es schwierig sein, die Abmessungen zu bestimmen, was in der Folge zu falschen Messungen und Volumenberechnungen führt. Indem Sie messen, wie viel Wasser von einem Objekt verdrängt wird, können Sie dessen Volumen ohne komplexe Formeln berechnen.
- Diese Methode kann auch verwendet werden, um das Volumen einer regelmäßigen Form zu berechnen.

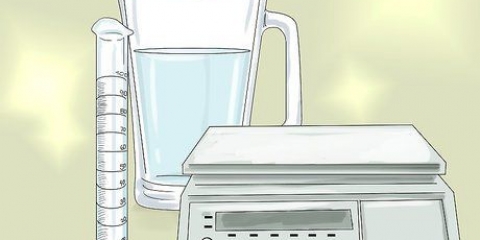
2. Füllen Sie einen Messzylinder mit Wasser. Ein Messzylinder ist ein Laborgerät mit Markierungen an der Außenseite und ermöglicht das Messen des Volumens einer bestimmten Flüssigkeitsmenge. Stellen Sie sicher, dass der Messzylinder groß genug ist, um das Objekt zu halten. Füllen Sie es mit so viel Wasser, dass das Objekt vollständig untergetaucht ist, aber das Wasser nicht über den Rand spritzt. Beachten Sie den Anfangsstand des Wassers.

3. Legen Sie das Objekt ruhig in die Tasse. Achten Sie darauf, das Objekt nicht ins Wasser fallen zu lassen, da sonst Wasser über den Rand fließen könnte und die Anzeige falsch ist. Stellen Sie sicher, dass das Objekt vollständig in Wasser eingetaucht ist. Beachten Sie den neuen Wasserstand der Tasse, wieder auf Augenhöhe, und achten Sie dabei genau auf den Meniskus.

4. Subtrahieren Sie den neuen Wasserstand vom Anfangsstand. Die vom Objekt verdrängte Wassermenge entspricht dem Volumen des Objekts, gemessen in Kubikzentimetern. Flüssigkeiten werden normalerweise in Millilitern gemessen, und ein Milliliter entspricht einem Kubikzentimeter.
Teil3 von 3: Berechnung der Dichte

1. Bestimmen Sie die Masse des Objekts. Die Menge an Materie in einem Objekt ist die Masse dieses Objekts. Dies kann direkt gemessen werden, indem das Objekt mit der Einheit in Gramm auf eine Waage gelegt wird.
- Halten Sie eine genaue Waage bereit und legen Sie das Objekt darauf. Notieren Sie seine Masse in Ihrem Notizbuch.
- Sie können die Masse auch mit einer Waage messen. Stellen Sie mit dem Objekt auf der einen Seite Gewichte bekannter Masse auf die andere Seite der Waage, bis sie mit dem Objekt im Gleichgewicht sind. Die Masse Ihres Objekts ist gleich der Gesamtmasse der Gewichte.
- Es ist wichtig, dass Ihr Artikel trocken ist, bevor Sie ihn wiegen. So können Sie sicher sein, dass das Messergebnis durch das aufgenommene Wasser nicht ungenauer wird.

2. Berechnen Sie das Volumen Ihres Objekts. Wenn Ihr Objekt eine regelmäßige Form hat, berechnen Sie das Volumen mit einer der zuvor angegebenen Methoden. Wenn die Form unregelmäßig ist, berechnen Sie das Volumen mit der oben erläuterten Verschiebungsmethode.

3. Berechnen Sie die Dichte. Dichte ist definiert als die Masse geteilt durch das Volumen. Um schließlich die Dichte zu bestimmen, dividieren Sie die gewichtete Masse durch das gemessene Volumen. Das Ergebnis ist die Dichte des Metalls ausgedrückt in g/cm.
 eines Stoffes mit einem Volumen von 8 cm und einer Masse von 24 g.
eines Stoffes mit einem Volumen von 8 cm und einer Masse von 24 g.
Tipps
- Sie können Ihre Volumenberechnungen testen, indem Sie das Ergebnis der Verschiebungsmethode und der Berechnungen vergleichen.
- Objekte sind oft eine Zusammenstellung mehrerer geometrischer Objekte, sodass Sie sie in kleinere Grundgruppen unterteilen können, um das Volumen jedes einzelnen zu bestimmen, und dann alle zusammenzählen, um das Volumen des Objekts zu bestimmen.
Warnungen
- Stellen Sie sicher, dass Sie alle Messungen in metrischen oder SI-Einheiten haben, bevor Sie mit Ihren Berechnungen fortfahren.
"Volumen und dichte berechnen"
Оцените, пожалуйста статью