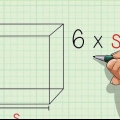
Dieser Vorgang ist im Grunde derselbe, wie zuerst die Fläche der Basis zu berechnen und dann diese Fläche mit der Höhe des Würfels zu multiplizieren (oder mit anderen Worten Länge × Breite × Höhe), da die Grundfläche durch Multiplikation der Länge mit der Breite bestimmt wird. Da Länge, Breite und Höhe eines Würfels gleich sind, können wir den Vorgang vereinfachen, indem wir einen dieser Werte mit der dritten Potenz erhöhen. Machen wir weiter mit unserem Beispiel. Die Kantenlänge betrug 2 cm, das Volumen des Würfels ist also 2 x 2 x 2 (oder 2)= 8. 
In unserem Beispiel wurde die Länge der Rippe in Zentimetern angegeben, die Antwort muss also in angegeben werden Kubikzentimeter. Die Antwort ist also 8 cm². 

In unserem Beispiel teilen wir also fünfzig durch sechs: 50/6 = 8,33 cm. Denken Sie daran, dass die Einheiten zweidimensionaler Antworten im Quadrat geschrieben werden (cm, m usw.). 
In unserem Beispiel ist √8.33 = 2,89 cm. 
In unserem Beispiel also: 2,89 × 2,89 × 2,89 = 24,14 cm. Vergiss nicht, die Antwort in Kubikeinheiten zu schreiben. 

Dies lässt sich auch aus dem Satz des Pythagoras ableiten. D, D und l Bilde ein gleichseitiges Dreieck mit D als Hypotenuse, also D = D + l. Zuvor hatten wir bereits festgestellt: D = 2l, also können wir auch folgendes sagen: D = 2l + l = 3l. Angenommen, wir wissen, dass die Länge der Diagonale von einer Ecke in der Basis des Würfels bis zur gegenüberliegenden Ecke in der Oberseite des Würfels 10 Meter beträgt. Wenn wir also das Volumen berechnen wollen, geben wir 10 in die obige Formel ein für D. D = 3l. 10 = 3l. 100 = 3l 33.33 = l 5.77 m² = l. Von diesem Punkt aus können wir das Volumen berechnen, indem wir die Länge der Rippe auf den Würfel erhöhen. 5.77 = 192.45 m
Das volumen eines würfels berechnen
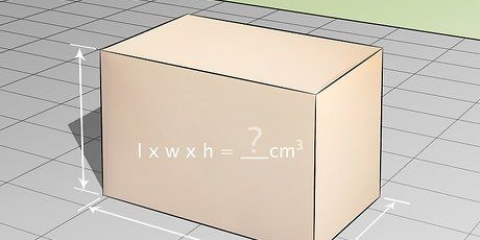
Ein Würfel ist eine dreidimensionale Figur, deren Länge, Breite und Höhe gleich sind. Ein Würfel hat sechs quadratische Flächen, deren Seiten gleich lang und senkrecht aufeinander stehen. Das Volumen eines Würfels zu berechnen ist sehr einfach - normalerweise müssen Sie nur Folgendes multiplizieren: Länge × Breite × Höhe. Da die Kanten eines Würfels alle die gleiche Länge haben, können Sie das Volumen eines Würfels auch wie folgt sehen: l, wodurch l ist die Länge einer der Kanten des Würfels. Gehen Sie zu Schritt 1 für eine detaillierte Erklärung.
Schritte
Methode 1 von 3: Anheben der Würfelkante zum Würfel

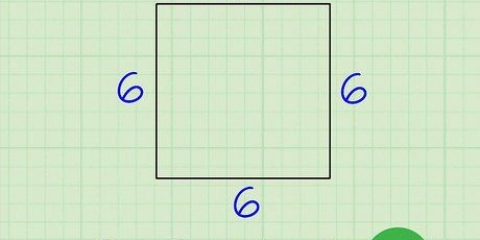
1. Finden Sie die Länge einer der Kanten des Würfels. Oft sehen Sie eine Summe, bei der die Länge einer der Rippen bereits angegeben ist. Sobald Sie diese Informationen haben, haben Sie alles, was Sie brauchen, um das Volumen des Würfels zu bestimmen. Verwenden Sie ein Lineal oder ein Maßband, wenn Sie kein mathematisches Problem lösen, sondern nur das Volumen eines vorhandenen würfelförmigen Objekts wissen möchten.
- Um den Prozess der Bestimmung des Volumens eines Würfels besser zu verstehen, beginnen wir mit einer Beispielsumme, während wir die Schritte in diesem Abschnitt durchlaufen. Angenommen, die Kante des Würfels 2 cm² lang ist. Wir werden diese Informationen im nächsten Schritt verwenden, um das Volumen des Würfels zu bestimmen.

2. Erhöhe die Länge der Rippe mit der dritten Potenz. Sobald Sie die Länge einer der Rippen haben, erhöhen Sie diese Zahl in die dritte Potenz. Mit anderen Worten, multiplizieren Sie die Zahl zweimal mit sich selbst. wenn l ist die Länge der Rippe, dann multipliziert man l × l × l (oder in einfacherer Form l). Das Ergebnis ist das Volumen des Würfels.

3. Geben Sie Ihre Antwort in Kubikeinheiten an. Das Volumen ist das Maß eines dreidimensionalen Raums, daher muss die Lösung in kubischen Einheiten geschrieben werden. Bei einem Test kann es Sie Punkte kosten, wenn Sie die Antwort nicht richtig in Kubikeinheiten angeben, also nicht vergessen!
Methode 2 von 3: Volumenbestimmung nach Oberfläche

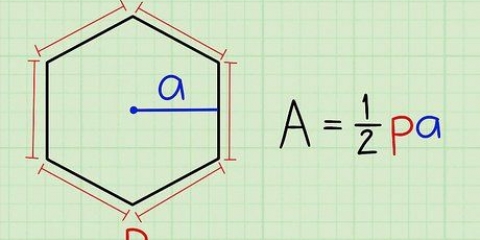
1. Finden Sie die Fläche der Flächen Ihres Würfels. Der am einfachsten Um das Volumen zu bestimmen, wird die Rippe zum Würfel angehoben, aber es ist nicht die beliebig Weg. Die Länge der Kante eines Würfels oder die Fläche einer seiner Seiten kann aus mehreren anderen Eigenschaften des Würfels abgeleitet werden, was bedeutet, dass Sie, wenn Sie mit diesen Informationen beginnen, das Volumen des Würfels auf abgeleitete Weise bestimmen können. Wenn Sie beispielsweise nur die Gesamtfläche aller Seiten des Würfels kennen, können Sie das Volumen ermitteln, indem Sie diese Fläche durch sechs teilen und dann die Quadratwurzel dieser Zahl ziehen, um die Länge der Kante zu ermitteln. Ab diesem Punkt kannst du wieder zur dritten Potenz erheben. In diesem Abschnitt gehen wir Schritt für Schritt durch diesen Prozess.
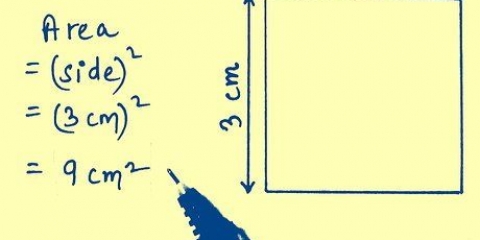
- Die Fläche eines Würfels ergibt sich aus der Formel 6l, wodurch l ist die Länge einer der Kanten des Würfels. Diese Formel entspricht eigentlich der Bestimmung der zweidimensionalen Fläche einer der Seiten des Würfels und der anschließenden Addition der sechs (gleichen) Flächen. Wir werden diese Formel verwenden, um das Volumen des Würfels aus der Fläche des Würfels zu bestimmen.
- Angenommen, wir haben einen Würfel, von dem wir wissen, dass die Fläche 50 cm² ist, aber wir wissen nicht, wie lang die Rippen sind. In den nächsten Schritten werden wir diese Informationen verwenden, um das Volumen des Würfels zu finden.

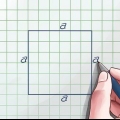
2. Teilen Sie die Fläche des Würfels durch sechs. Da der Würfel sechs flächengleiche Flächen hat, können wir die Fläche einer Fläche bestimmen, indem wir die Fläche des Würfels durch sechs teilen. Die Fläche einer Ebene entspricht der Multiplikation zweier Kanten (l × b, b × h oder h × l).

3. Finden Sie die Quadratwurzel dieses Wertes. Da die Fläche einer der Flächen eines Würfels gleich ist l (l × l), können wir nun die Quadratwurzel des gefundenen Wertes ziehen, um die Länge einer der Rippen zu bestimmen. Sobald Sie dies wissen, haben Sie genügend Informationen, um das Volumen des Würfels wie gewohnt zu berechnen.

4. Erhöhe diese Zahl mit der dritten Potenz, um das Volumen des Würfels zu bestimmen. Nachdem Sie nun einen Wert für die Länge der Rippen ermittelt haben, können Sie diese Zahl auf den Würfel erhöhen, um das Volumen zu bestimmen, wie im ersten Abschnitt dieses Artikels beschrieben.
Methode 3 von 3: Volumenbestimmung mit Diagonalen

1. Teilen Sie die Diagonale einer der Seiten des Würfels durch √2, um die Länge der Kanten des Würfels zu ermitteln. Die Diagonale eines Quadrats ist √2 × die Länge einer seiner Kanten. Mit anderen Worten, wenn Sie nur den Wert einer der Diagonalen einer Würfelfläche kennen, können Sie die Länge der Kanten des Würfels berechnen, indem Sie diesen Wert durch √2 . dividieren. Ab diesem Punkt können Sie wieder in die dritte Potenz erhöhen und die Lautstärke wie oben beschrieben bestimmen.
- Angenommen, eine der Seiten des Würfels hat eine Diagonale von7 Meter lang. Dann können wir die Länge einer der Rippen berechnen, indem wir 7 durch √2 . teilen. 7/√2 = 4,96 Meter. Da wir nun die Länge der Kanten des Würfels kennen, können wir das Volumen des Würfels berechnen, indem wir 4,96 zum Würfel erhöhen: 4,96 = 122,36 Meter.
- Passt auf: D = 2l, wahr D die Länge der Diagonale einer der Seiten des Würfels ist und l ist die Länge einer der Kanten des Würfels. Dies kann aus dem Satz des Pythagoras abgeleitet werden, wobei das Quadrat der Hypotenuse eines gleichseitigen Dreiecks gleich der Summe der Quadrate der anderen beiden Seiten ist. Da die Diagonale einer Fläche eines Würfels mit zwei der Kanten dieser Fläche ein gleichseitiges Dreieck bildet, können wir Folgendes sagen: D = l + l = 2l.

2. Finde das Quadrat der Diagonale zwischen zwei gegenüberliegenden Ecken des Würfels, dividiere durch drei und ziehe die Quadratwurzel, um die Länge einer der Kanten zu bestimmen. Wenn nur die Länge der dreidimensionalen Linie zwischen zwei gegenüberliegenden Ecken des Würfels gegeben ist, können Sie noch das Volumen des Würfels bestimmen. D bildet eine der Seiten eines gleichseitigen Dreiecks, dessen Hypotenuse die Linie zwischen zwei gegenüberliegenden Ecken des Würfels ist, also können wir sagen: D = 3l, wobei D die dreidimensionale Linie zwischen zwei gegenüberliegenden Ecken des Würfels ist.
Оцените, пожалуйста статью