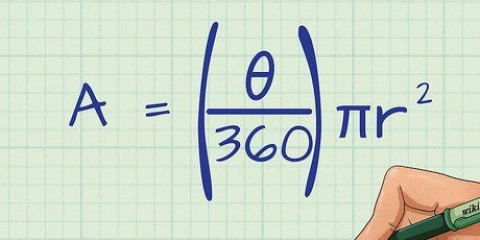Sehen Sie das Apothem als das "x√3"-Seite eines 30-60-90-Dreiecks. Sie können es so sehen, weil das Sechseck aus sechs gleichseitigen Dreiecken besteht. Das Apothem schneidet eines dieser Dreiecke in zwei Hälften, wodurch ein Dreieck mit Winkeln von 30, 60 und 90 Grad entsteht. Sie wissen, dass die dem 60-Grad-Winkel gegenüberliegende Seite eine Länge von x√3 hat, die dem 30-Grad-Winkel gegenüberliegende Seite eine Länge von x hat und die dem 90-Grad-Winkel gegenüberliegende Seite eine Länge von 2x . hat. Wenn 10√3 für steht "x√3," dann wissen Sie, dass x = 10. Sie wissen, dass x die halbe Länge der Unterseite des Dreiecks ist. Verdoppeln Sie dies, um die volle Länge zu bestimmen. Die Unterseite des Dreiecks ist also 20. Es gibt sechs dieser Seiten im Sechseck. Um den Umfang des Sechsecks zu ermitteln, multiplizieren wir 20 mit 6 = 120. 
Fläche = 1/2 x 120 x 10√3 Fläche = 60 x 10√3 Fläche = 600√3 


Wenn Sie ein Quadrat mit einer Seitenlänge von 6 haben, ist die Fläche 6 x 6 = 36. 
Wenn die Grundfläche eines Rechtecks 4 und die Höhe 3 beträgt, dann ist die Fläche 4 x 3 = 12. 
Angenommen, Sie haben ein Trapez, dessen Basen die Längen 6 und 8 haben und dessen Höhe 10 . beträgt. Dann ist die Fläche [(6 + 8) x 10]/2, was vereinfacht werden kann zu (14 x 10)/2 oder 140/2, was einer Fläche von 70 . entspricht. 





Berechnen sie die fläche eines polygons
Die Berechnung der Fläche eines Polygons kann sehr einfach sein, wenn es um ein regelmäßiges Dreieck geht. Bei einer unregelmäßigen Form mit elf Seiten wird es jedoch viel schwieriger. Wenn Sie wissen möchten, wie Sie die Fläche verschiedener Polygone berechnen, folgen Sie diesen Schritten.
Schritte
Teil 1 von 3: Berechnung der Fläche von Polygonen mit dem Apothem

1. Schreiben Sie die Formel zum Ermitteln der Fläche eines regelmäßigen Vielecks. Um die Fläche eines regelmäßigen Polygons zu ermitteln, müssen Sie nur der Formel folgen: Fläche = 1/2 x Umfang x Apothem. Das bedeutet folgendes:
- Umfang = Summe der Längen aller Seiten
- Apothem = das Segment und auch der Abstand vom Mittelpunkt des Polygons zum Mittelpunkt einer Seite

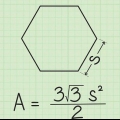
2. Bestimme das Apothem des Polygons. Wenn Sie die Apothem-Methode verwenden, ist das Apothem immer gegeben. Angenommen, Sie arbeiten mit einem Sechseck, dessen Apothem eine Länge von 10√3 . hat.

3. Bestimmen Sie den Umfang des Polygons. Wenn der Umfang vorgegeben ist, bist du fast fertig. Aber wohl nur das Apothem ist gegeben. Wenn Sie wissen, dass es sich um ein regelmäßiges Vieleck handelt, können Sie seinen Umfang mit dem Apothem bestimmen. So machst du das:

4. Jetzt können wir das Apothem und den Umfang in die Formel einfügen. Noch einmal: Fläche = 1/2 x Umfang x Apothem, der Umfang ist 120 und das Apothem ist 10√3. Dann sieht die Formel so aus:

5. Vereinfache deine Antwort. Vielleicht solltest du das Ergebnis in Dezimalzahlen statt in einem Radikal schreiben. Verwenden Sie Ihren Taschenrechner, um die ungefähre Quadratwurzel von drei zu finden und diese mit 600 . zu multiplizieren. √3 x 600 = 1.039.2. Das ist das Ergebnis in Dezimalzahlen.
Teil 2 von 3: Ermitteln der Fläche eines regelmäßigen Vielecks mit anderen Formeln

1. Berechnen Sie die Fläche eines geraden Dreiecks. Wenn Sie die Fläche eines regelmäßigen Dreiecks ermitteln möchten, können Sie diese Formel verwenden: Fläche = 1/2 x Basis x Höhe.
- Wenn Sie ein Dreieck mit einer Basis von 10 und einer Höhe von 8 haben, dann ist die Fläche = 1/2 x 8 x 10 = 40.

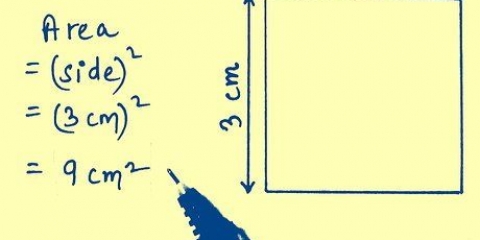
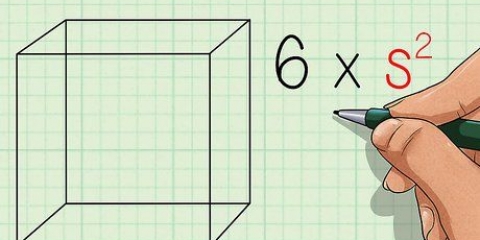
2. Berechnen Sie die Fläche eines Quadrats. Um die Fläche eines Quadrats zu ermitteln, musst du nur eine seiner Seiten mit sich selbst multiplizieren, da Grundfläche und Höhe für ein Quadrat gleich sind.

3. Berechnen Sie die Fläche eines Rechtecks. Um die Fläche eines Rechtecks zu finden, musst du nur seine Grundfläche mit seiner Höhe multiplizieren.

4.Berechnen Sie die Fläche eines Trapezes. Um die Fläche eines Trapezes zu ermitteln, können Sie die folgende Formel verwenden: Fläche = [(Basis 1 + Basis 2) x Höhe]/2.
Teil 3 von 3: Finden der Fläche eines unregelmäßigen Polygons

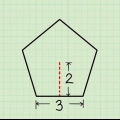
1. Verwenden Sie die Koordinaten der Knoten, um die Fläche zu berechnen. Wenn Sie die Koordinaten kennen, können Sie die Fläche eines unregelmäßigen Polygons berechnen.

2. Erstellen Sie eine Sequenz. Listen Sie die x- und y-Koordinaten jedes Eckpunkts des Polygons gegen den Uhrzeigersinn auf. Wiederholen Sie die Koordinaten des ersten Punktes am Ende der Liste.

3. Multiplizieren Sie die x-Koordinate jedes Eckpunkts mit der y-Koordinate des nächsten Eckpunkts. Addiere die Ergebnisse. Die Summe dieser Produkte beträgt 82.

4. Multiplizieren Sie die y-Koordinate jedes Scheitelpunkts mit der x-Koordinate des nächsten Scheitelpunkts. Addiere die Ergebnisse. Die Summe dieser Produkte beträgt -38.

5. Subtrahiere die Summe der in Schritt 4 berechneten Produkte von der Summe der in Schritt 3 berechneten Produkte. (82) - (-38) = 120.

6. Teilen Sie dieses Ergebnis durch 2, um die Fläche des Polygons zu finden. Fläche = 120/2 = 60.
Tipps
- Wenn Sie die Punkte im Uhrzeigersinn statt gegen den Uhrzeigersinn auflisten, erhalten Sie auch die Fläche, aber negativ. Sie können dies beispielsweise als Werkzeug verwenden, um die zyklische Abfolge einer Menge von Punkten zu bestimmen, die ein Polygon bilden.
- Diese Formel berechnet die Fläche mit Orientierung. Wenn Sie es auf einer Form verwenden, bei der sich zwei der Linien wie in einer 8 schneiden, erhalten Sie den Bereich gegen den Uhrzeigersinn minus den Bereich im Uhrzeigersinn.
"Berechnen sie die fläche eines polygons"
Оцените, пожалуйста статью