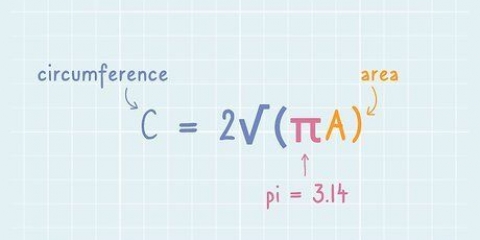Angenommen, der Zentralwinkel beträgt 100 Grad, dann dividieren Sie 100 durch 360 und erhalten somit 0,28. Die Fläche des Segments beträgt also etwa 28 Prozent der Fläche des gesamten Kreises. Wenn Sie den Mittelpunktswinkel nicht kennen, aber wissen, welcher Teil des Kreises das Segment ist, finden Sie den Winkel, indem Sie diesen Bruchteil mit 360 . multiplizieren. Wenn Sie beispielsweise wissen, dass das Segment ein Viertel des Kreises ist, multiplizieren Sie 360 mit einem Viertel (0,25), um 90 Grad zu erhalten. 
Wenn der Radius beispielsweise 5 cm beträgt, berechnen Sie 5 x 5 = 25 und dann 25 x 3,14 = 78,5. Wenn Sie die Länge des Radius nicht kennen, aber den Durchmesser kennen, teilen Sie den Durchmesser durch zwei, um den Radius zu ermitteln. 
Zum Beispiel: 0,28 x 78,5 = 21,89. Da Sie die Fläche berechnen, sollte Ihre Antwort in Quadratzentimetern ausgedrückt werden.. 

Wenn beispielsweise die Bogenlänge 5 cm und der Radius 8 cm beträgt, beträgt Ihr neuer Zähler 40 Zoll. 
Zum Beispiel:  .
. Da Sie die Fläche berechnen, sollte Ihre Antwort in Quadratzentimetern ausgedrückt werden.
Berechnen sie die fläche eines segments
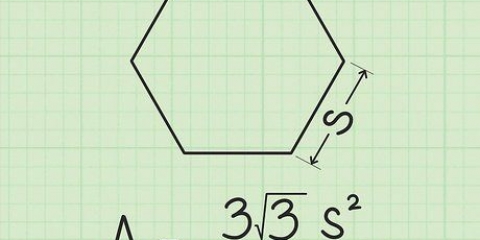
Manchmal ist es notwendig, die Fläche unter einem Bogen oder die Fläche eines Segments zu bestimmen. Ein Segment ist ein Teil eines Kreises, der wie ein Stück Pizza oder Kuchen geformt ist. Um die Fläche dieses Stücks zu finden, müssen Sie die Länge des Radius des Kreises kennen. Neben dem Radius müssen Sie entweder den Mittelpunktswinkel in Grad oder die Länge des Bogens kennen. Bei diesen Messungen ist die Bestimmung der Fläche eines Segments eine einfache Sache, die Zahlen in feste Formeln zu füllen.
Schritte
Methode 1 von 2: Berechnen Sie die Fläche, deren Mittelpunktswinkel und Radius bekannt sind

1. Stellen Sie die Formel auf: . In der Formel ist r der Radius und θ die Gradzahl des Mittelpunktswinkels des Segments.
. In der Formel ist r der Radius und θ die Gradzahl des Mittelpunktswinkels des Segments.
 . In der Formel ist r der Radius und θ die Gradzahl des Mittelpunktswinkels des Segments.
. In der Formel ist r der Radius und θ die Gradzahl des Mittelpunktswinkels des Segments. - Denken Sie daran, dass die Fläche eines Kreises gleich ist
. Wenn Sie die Fläche eines Segments bestimmen, berechnen Sie wirklich nur die Fläche des gesamten Kreises und multiplizieren diese dann mit dem Bruchteil des Kreises, den das Segment darstellt.
- Ein Kreis hat 360 Grad, wenn Sie also den Mittelwinkel des Segments als Bruch über 360 setzen, erhalten Sie den Teil des ganzen Kreises.

2. Geben Sie den Mittelpunktswinkel des Segments in die Formel ein. Teilen Sie den Zentralwinkel durch 360. Dadurch erhalten Sie den Teil oder den Prozentsatz des gesamten Kreises, den das Segment darstellt.

3. Geben Sie den Radius in die Formel ein. Quadrieren Sie den Radius und multiplizieren Sie die Antwort mit 𝝅 (3.14). Berechnet die Fläche des ganzen Kreises.

4. Multipliziere die beiden Zahlen miteinander. Du multiplizierst den Prozentsatz noch einmal mit der Fläche des ganzen Kreises. Dadurch erhalten Sie die Fläche des Segments.
Methode 2 von 2: Berechnen Sie die Fläche mit bekannter Bogenlänge und Radius

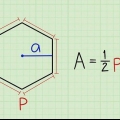
1. Stellen Sie die Formel auf: . In der Formel ist r die Länge des Radius und l = die Länge des Bogens.
. In der Formel ist r die Länge des Radius und l = die Länge des Bogens.
 . In der Formel ist r die Länge des Radius und l = die Länge des Bogens.
. In der Formel ist r die Länge des Radius und l = die Länge des Bogens. - Verwenden Sie die Formel, um den Umfang eines Kreises zu ermitteln: 2𝝅r. Wenn Sie die Länge des Bogens (der Teil des Umfangs ist) kennen, können Sie bestimmen, welchen Teil des Kreises das Segment darstellt, indem Sie die Bogenlänge mit dem Gesamtumfang vergleichen.
- Die vollständige Formel lautet dann:
-- Sie können dies jedoch vereinfachen zu
.

2. Geben Sie die Bogenlänge und den Radius in die Formel ein. Sie werden diese beiden Zahlen multiplizieren, um einen neuen Zähler zu erhalten.

3. Durch zwei teilen. Sie teilen den Zähler, den Sie in Schritt zwei finden. Dadurch erhalten Sie die Fläche des Segments.
 .
. "Berechnen sie die fläche eines segments"
Оцените, пожалуйста статью