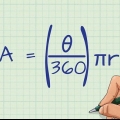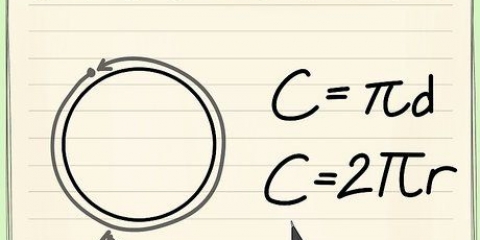Nehmen wir an, die Fläche des Kreises beträgt 500 cm. Dann stellst du die Gleichung wie folgt auf: 2√3.14 x 500. 
Wenn die Berechnung gleich 2√3.14 x 500 ist, berechnen Sie zuerst 3.14 x 500 = 1570. Dann berechne 2√1.570. 
Die Quadratwurzel von 1570 ist 39,6. 
Berechnen Sie 39,6 x 2 = 79,2. Dies bedeutet, dass der Umfang 79,2 cm beträgt, was die Formel löst. 

Angenommen, die Fläche des Kreises beträgt 200 cm. Die Gleichung wird dann 200 = 3,14 x R. 
Wenn Sie 200 durch 3,14 dividieren, ist das Ergebnis 63,7. Die neue Gleichung lautet also 63,7 = R. 
Die Quadratwurzel von 63,7 ist 7,9. Die Gleichung wird dann 7,9 = R, was bedeutet, dass der Radius des Kreises 7,9 . beträgt. Dadurch erhalten Sie alle Informationen, die Sie benötigen, um den Perimeter zu finden. 
Verwenden Sie die erste Option, 7,9 x 2 = 15,8, den Durchmesser des Kreises. Dieser Durchmesser mal 3,14 ist 49,6. Für die zweite Option beträgt die Berechnung 2 x 3,14 x 7,9. Zuerst berechnen Sie 2 x 3,14 = 6,28, und das multipliziert mit 7,9 ergibt 49,6. Beachten Sie, wie beide Methoden Ihnen die gleiche Antwort geben.
Berechnen sie den umfang mit der fläche
Die Formel zur Berechnung des Umfangs (C) eines Kreises, C = πD oder C = 2πR, ist einfach, wenn Sie den Durchmesser (D) oder Radius (R) des Kreises kennen. Aber was macht man, wenn man nur die Fläche des Kreises kennt? Wie für viele Dinge in der Mathematik gibt es mehrere Lösungen für dieses Problem. Die Formel C = 2√πA soll den Umfang eines Kreises mit der Fläche (A) ermitteln. Sie können auch die Gleichung A = πR umkehren, um R zu finden, und dann R in die Umfangsgleichung eingeben. Beide Gleichungen liefern das gleiche Ergebnis.
Schritte
Methode 1 von 2: Verwenden der Umfangsgleichung

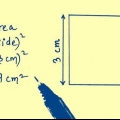
1. Verwenden Sie die Formel C=2√πA, um das Problem zu lösen. Diese Formel berechnet den Umfang eines Kreises, wenn Sie nur seine Fläche kennen. C steht für den Umfang und A für die Fläche. Schreiben Sie diese Formel, um mit der Lösung des Problems zu beginnen.
- Das π-Symbol, das für Pi steht, ist eine sich wiederholende Dezimalzahl mit (inzwischen) Tausenden von Nachkommastellen. Verwenden Sie der Einfachheit halber 3,14 als Wert von pi.
- Da Sie Pi sowieso in seine numerische Form umwandeln müssen, verwenden Sie von Anfang an 3.14 in der Gleichung. Schreiben Sie es als C = 2√3.14 x A.

2. Beziehe die Fläche als A in die Gleichung ein. Da Sie die Fläche des Kreises bereits kennen, ist das der Wert von A. Fahren Sie dann mit der Lösung des Problems in der Reihenfolge der Operationen fort.

3. Multiplizieren Sie pi mit der Fläche des Kreises. In der Reihenfolge der Operationen stehen die Operationen innerhalb des Quadratwurzelsymbols an erster Stelle. Multiplizieren Sie pi mit der Fläche des Kreises, den Sie eingesteckt haben. Setze das Ergebnis dann in die Gleichung ein.

4. BesondereQuadratwurzel der Summe. Es gibt mehrere Möglichkeiten, die Quadratwurzel zu berechnen. Wenn Sie einen Taschenrechner verwenden, drücken Sie die Funktion √ und geben Sie die Zahl ein. Sie können das Problem auch von Hand mit Primfaktoren lösen.

5. Multiplizieren Sie die Quadratwurzel mit 2, um den Umfang zu finden. Schließlich vervollständigen Sie die Berechnung, indem Sie das Ergebnis mit 2 . multiplizieren. Dies gibt eine letzte Zahl zurück, den Umfang.
Methode 2 von 2: Beheben Sie das Problem umgekehrt

1. Verwenden Sie die Formel A = πR in. Das ist die Formel für die Fläche eines Kreises. A steht für die Fläche und R für den Radius. Normalerweise würden Sie es verwenden, wenn Sie den Radius kennen, aber Sie können auch die Fläche ausfüllen, um die Gleichung zu lösen.
- Verwenden Sie wieder 3,14 als gerundeten Wert für pi.

2. Geben Sie die Fläche als Wert für A . ein. Verwenden Sie die Fläche des Kreises in der Gleichung. Setzen Sie dies links von der Gleichung als Wert für A.

3. Teilen Sie beide Seiten der Gleichung durch 3,14. Um diese Art von Gleichung zu lösen, müssen Sie die Schritte auf der rechten Seite schrittweise eliminieren, indem Sie die entgegengesetzten Operationen ausführen. Da Sie den Wert von pi kennen, dividieren Sie jede Seite durch diesen Wert. Dadurch wird Pi auf der rechten Seite eliminiert und Sie erhalten einen neuen numerischen Wert auf der linken Seite.

4. BesondereQuadratwurzel des Ergebnisses, um den Radius des Kreises zu erhalten. Dann wird der Exponent auf der rechten Seite der Gleichung eliminiert. Das Gegenteil von `Exponentiation` ist das Finden der Quadratwurzel der Zahl. Finden Sie die Quadratwurzel jeder Seite der Gleichung. Dies entfernt den Exponenten rechts und setzt den Radius links.

5.Bestimmen Sie den Umfang des Kreises mit dem Radius. Es gibt zwei Formeln, um den Umfang (C) zu finden. Die erste ist C = πD, wobei D der Durchmesser ist. Multiplizieren Sie den Radius mit 2, um den Durchmesser zu finden. Die zweite ist C = 2πR. Multiplizieren Sie 3,14 mit 2 und multiplizieren Sie dann das Ergebnis mit dem Radius. Beide Formeln liefern das gleiche Ergebnis.
"Berechnen sie den umfang mit der fläche"
Оцените, пожалуйста статью