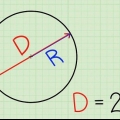
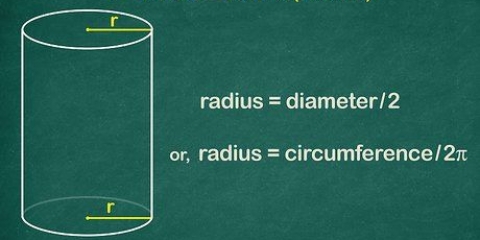
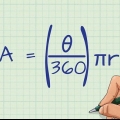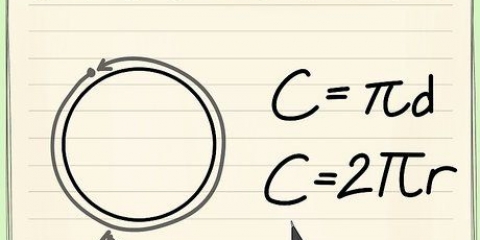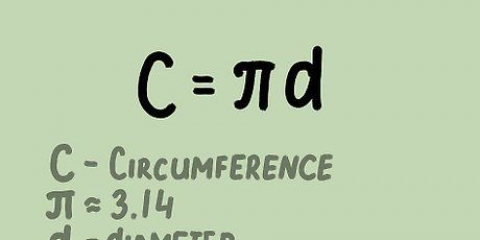Wenn Sie versuchen, eine Story-Summe zu lösen, ist der Radius möglicherweise bereits angegeben. Vielleicht gibt die Summe bereits den Durchmesser an, oder den Abstand zwischen einer Seite des Kreises und der anderen Seite des Kreises, der durch den Mittelpunkt geht. Der Radius ist genau der halbe Durchmesser. Sie können den Radius mit einem Lineal messen, wenn Sie die Fläche eines echten Zylinders berechnen möchten. 
Um die Fläche des oberen Kreises zu berechnen, geben Sie einfach den Radius (3 Zentimeter) in die Gleichung zur Berechnung der Fläche eines Kreises ein. A = r. So machst du das: A = r A = π x 3 A = π x 9 = 28,26 cm 






Berechnen sie die fläche eines zylinders
Die Fläche eines Zylinders ist die Summe der Flächen der Ober-, Unter- und Seitenwände. Um die Fläche eines Zylinders zu berechnen, müssen Sie die Fläche der kreisförmigen Ober- und Unterseite berechnen und diese Zahl zur Fläche der Seitenwand hinzufügen. Die Formel zur Berechnung der Fläche eines Zylinders lautet A = 2πr + 2πrh.
Schritte
Teil 1 von 3: Berechnung der Fläche der Kreise (2 x (π x r))

1. Stellen Sie sich die Ober- und Unterseite eines Zylinders vor. Eine Dose Suppe hat die Form eines Zylinders. Wenn Sie darüber nachdenken, werden Sie feststellen, dass die Dose oben und unten gleich ist. Sowohl die Ober- als auch die Unterseite haben die Form eines Kreises. Der erste Schritt bei der Berechnung der Fläche des Zylinders besteht darin, die Fläche beider kreisförmiger Enden zu berechnen.

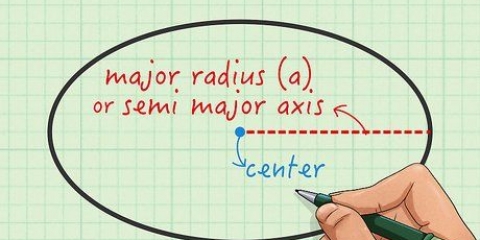
2. Finden Sie den Radius des Zylinders. Der Radius oder Radius ist der Abstand zwischen dem Mittelpunkt eines Kreises und dem äußeren Rand dieses Kreises. Der Radius wird durch den Buchstaben angegeben "R". Der Radius Ihres Zylinders ist der gleiche wie der Radius des oberen und unteren Kreises. In diesem Beispiel beträgt der Radius der Basis 3 Zentimeter.

3. Berechnen Sie die Fläche des oberen Kreises. Die Fläche eines Kreises ist gleich der Zahl pi (~3.14) multipliziert mit dem Radius des Kreises zum Quadrat. Die Gleichung wird geschrieben als π x r. Dies ist dasselbe wie π x r x r.

4. Machen Sie dasselbe für den Kreis auf der anderen Seite. Nachdem Sie nun die Fläche eines der Kreise berechnet haben, müssen Sie auch die Fläche des anderen Kreises berechnen. Sie können die gleichen Schritte wie beim ersten Kreis ausführen, oder Sie können sehen, dass beide Kreise identisch sind. Wenn Sie das verstanden haben, müssen Sie die Berechnung für den zweiten Kreis nicht erneut durchführen.
Teil 2 von 3: Berechnung der Seitenwandfläche (2π x r x h)

1. Stellen Sie sich die Seitenwand eines Zylinders vor. Wenn Sie sich eine zylindrische Suppendose vorstellen, sollten Sie oben und unten einen Boden sehen. Diese Flächen sind durch eine Seitenwand aus Zinn miteinander verbunden. Der Radius der Seitenwand ist der gleiche wie der Radius der Basen, aber die Seitenwand hat eine Höhe und die Basen nicht.

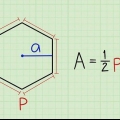
2. Finden Sie den Umfang eines der Kreise. Sie müssen diesen Umfang berechnen, um die Fläche der Seitenwand (auch als seitliche Fläche bezeichnet) zu ermitteln. Um den Umfang zu berechnen, multiplizieren Sie einfach den Radius mit 2π. Sie können also die Fläche berechnen, indem Sie 3 Zentimeter mit 2π . multiplizieren. 3 Zentimeter x 2π = 18,84 Zentimeter.

3. Multiplizieren Sie den Umfang des Kreises mit der Höhe des Zylinders. Du bekommst dann die Fläche der Seitenwand. Multiplizieren Sie den Umfang (18,84 Zentimeter) mit der Höhe (5 Zentimeter). 18,84 Zentimeter x 5 Zentimeter = 94,2 cm.
Teil 3 von 3: Berechnung der Gesamtfläche ((2) x (π x r)) + (2π x r x h)

1. Stell dir den kompletten Zylinder vor. Zuerst stellte man sich vor, wie die kreisförmige Ober- und Unterseite aussah und berechnete die Fläche beider Kreise. Dann hast du über die Seitenwand nachgedacht, die beide Kreise verbindet und deren Fläche berechnet. Versuchen Sie sich jetzt die gesamte Dose vorzustellen, weil Sie jetzt die Fläche des gesamten Zylinders berechnen werden.

2. Berechnen Sie die Fläche beider Kreise zusammen. Multiplizieren Sie einfach das vorherige Ergebnis (28,26 cm) mit 2, um die Fläche beider Kreise zusammen zu berechnen. 28,26 x 2 = 56,52 cm. Das ist die Fläche beider Kreise.

3. Addiere die Fläche der Seitenwand und die Fläche beider Kreise zusammen. Wenn Sie die Fläche beider Kreise zur Fläche der Seitenwand addiert haben, haben Sie die Fläche des gesamten Zylinders berechnet. Sie müssen nur 56,52 cm (die Fläche beider Kreise zusammen) und 94,2 cm (die Fläche der Seitenwand) hinzufügen. 56,52 cm + 94,2 cm = 150,72 cm. Die Fläche eines Zylinders mit einer Höhe von 5 Zentimetern und einer kreisförmigen Grundfläche mit einem Radius von 3 Zentimetern beträgt also 150,72 cm.
Tipps
- Wenn es eine Quadratwurzel in Höhe oder Radius gibt, finden Sie heraus, wie man Quadratwurzeln multipliziert, subtrahiert und addiert, um mehr darüber zu erfahren. Du kannst auch deinen Lehrer fragen.
Warnungen
- Denken Sie daran, die Fläche der kreisförmigen Basis immer mit 2 zu multiplizieren, um auch die Fläche des zweiten Kreises einzubeziehen.
"Berechnen sie die fläche eines zylinders"
Оцените, пожалуйста статью