Wenn Sie den Umfang kennen, teilen Sie ihn durch 6, um die Länge einer Seite zu berechnen. Zum Beispiel: die Länge des Umfangs beträgt 54 cm; dividiere diese durch 6 und du erhältst 9 cm als Antwort für die Seitenlänge.
Wenn Sie nur das Apothem kennen, können Sie die Länge einer Seite ermitteln, indem Sie den Wert des Apothems in die Formel eingeben a = x√3 und multipliziere die Antwort mit 2. Dies liegt daran, dass das Apothem die Seite eines 30-60-90-Dreiecks bildet. Wenn das Apothem beispielsweise 10√3 ist, dann ist x gleich 10 und die Länge einer Seite ist 10 x 2 = 20. 

(3√3 x 9)/2 = (3√3 x 81)/2 = (243√3)/2 = 420.8/2 = 210.4 cm 


Das Apothem ist die Seite x√3. Deshalb können Sie diesen Wert in die Formel eintragen a = x√3. Wenn die Länge des Apothems beispielsweise 5√3 beträgt, dann gemäß der Formel: 5√3 cm = x√3 oder x = 5 cm. Durch Lösen von x haben Sie die Länge der kurzen Seite des Dreiecks gefunden, x = 5. Da dies die halbe Länge einer Seite des Sechsecks ist, können Sie dies mit 2 multiplizieren, um die volle Länge der Seite zu erhalten. 5cm x 2 = 10cm. Jetzt, da Sie wissen, dass die Gesamtlänge einer Seite 10 beträgt, müssen Sie sie nur noch mit 6 multiplizieren, um den Umfang des Sechsecks zu erhalten. 10cm x 6 = 60cm 
Fläche = 1/2 x Umfang x Apothem Fläche = 1/2 x 60 cm x 5√3 cm 
1/2 x 60cm x 5√3cm = 30 x 5√3 cm = 150√3 cm = 259. 8 cm² 

4 x 7 = 28 9 x 2 = 18 11 x 2 = 22 2 x 5 = 10 1 x 7 = 7 4 x 10 = 40 28 + 18 + 22 + 10 + 7 + 40 = 125 
10 x 9 = 90 7 x 11 = 77 2 x 2 = 4 2 x 1 = 2 5 x 4 = 20 7 x 4 = 28 90 + 77 + 4 + 2 + 20 + 28 = 221 




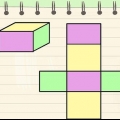
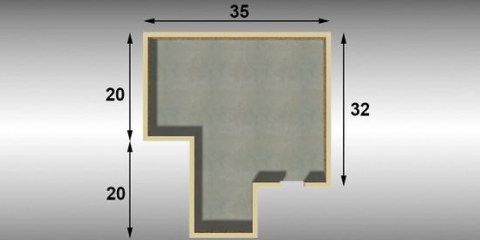
Eine bestimmte Art von unregelmäßigem Sechseck besteht aus zwei Parallelogrammen. Um deren Flächen zu berechnen, multiplizieren Sie die Basis mit der Höhe, genau wie bei einem Rechteck, und addieren Sie dann ihre Flächen zusammen.
Berechnen sie die fläche eines sechsecks
- Schritte
- Methode 1 von 4: Die Fläche eines regelmäßigen Sechsecks mit einer gegebenen Seite
- Methode 2 von 4: Die Fläche eines regelmäßigen Sechsecks mit einem bekannten Apothem
- Methode 3 von 4: Berechnen Sie die Fläche eines ungeraden Sechsecks mit gegebenen Eckpunkten
- Methode 4 von 4: Andere Methoden zur Berechnung der Fläche eines Hexagons
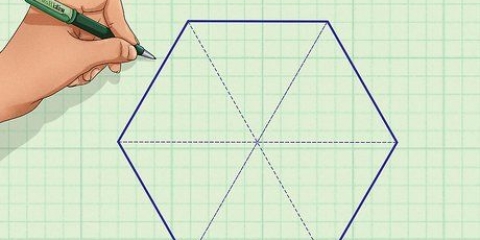
Ein Sechseck oder Sechseck ist ein Vieleck mit sechs Seiten und Winkeln. Ein regelmäßiges Sechseck hat sechs gleiche Seiten und Winkel und besteht aus sechs gleichseitigen Dreiecken. Es gibt verschiedene Möglichkeiten, die Fläche eines unregelmäßigen oder regelmäßigen Sechsecks zu berechnen. Wenn Sie wissen möchten, wie, folgen Sie diesen Schritten.
Schritte
Methode 1 von 4: Die Fläche eines regelmäßigen Sechsecks mit einer gegebenen Seite

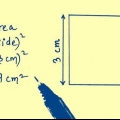
1. Schreiben Sie die Formel zur Berechnung der Fläche eines Sechsecks auf, wenn Sie die Länge einer Seite kennen. Da ein regelmäßiges Sechseck aus sechs gleichseitigen Dreiecken besteht, leitet sich die Formel zum Ermitteln der Fläche eines Sechsecks aus der Formel zur Berechnung der Fläche eines gleichseitigen Dreiecks ab. Die Formel dafür lautet: Fläche = (3√3 s)/ 2 wobei` die Länge einer Seite des regelmäßigen Sechsecks ist.

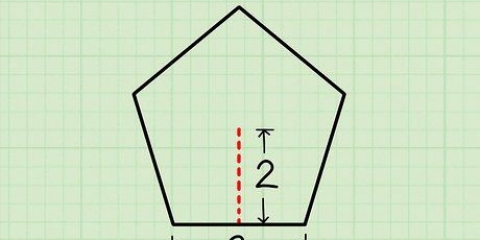
2. Bestimmen Sie die Länge der Seite. Wenn Sie die Länge bereits kennen, schreiben Sie sie auf. In diesem Fall beträgt die Länge einer Seite 9 cm. Wenn Sie die Länge nicht kennen, aber wissen, wie lang der Umfang ist, oder Sie das Deapothem kennen (die Länge der Linie von der Mitte des Sechsecks, die senkrecht zu einer Seite steht), können Sie immer noch die Länge der Seite ermitteln eines berechneten Sechsecks. So geht`s:

3. Geben Sie die Länge der Seite in die Formel ein. Da Sie wissen, dass die Länge einer Seite des Dreiecks 9 beträgt, können Sie dies einfach in die ursprüngliche Formel einsetzen. Es sieht so aus: Fläche = (3√3 x 9)/2

4. Vereinfache deine Antwort. Finden Sie den Wert der Gleichung und schreiben Sie Ihre Antwort auf. Denken Sie daran, da Sie die Fläche berechnen, sollte die Antwort in Quadratmetern sein. Hier kannst du nachlesen, wie das geht
Methode 2 von 4: Die Fläche eines regelmäßigen Sechsecks mit einem bekannten Apothem

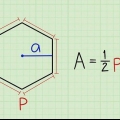
1. Schreiben Sie die Formel zur Berechnung der Fläche eines Sechsecks mit einem gegebenen Apothem auf. Die Formel ist einfach: Fläche = 1/2 * Umfang * Apothem.

2. Beachte das Apothem. Angenommen, das Apothem ist 5√3 cm . groß.

3. Verwenden Sie das Apothem, um den Umfang zu finden. Da das Apothem senkrecht zur Seite des Sechsecks steht, bildet es eine Seite eines 30-60-90-Dreiecks. Die Seiten eines 30-60-90-Dreiecks haben das Verhältnis: xx√3-2x, wobei x die Länge der kürzesten Seite (entgegen dem Winkel von 30 Grad) ist, x√3 die Länge der langen Seite (entgegengesetzt der Winkel von 60 Grad) und 2x die Hypotenuse.

4. Tragen Sie alle bekannten Werte in die Formel ein. Den Umfang zu berechnen war der schwierigste Teil. Jetzt müssen Sie nur noch das Apothem und den Umfang mit der Formel lösen:

5. Vereinfache deine Antwort. Vereinfachen Sie den Ausdruck, bis Sie alle Quadratwurzeln aus der Gleichung entfernt haben. Stellen Sie sicher, dass Ihre endgültige Antwort in Quadratmetern ist.
Methode 3 von 4: Berechnen Sie die Fläche eines ungeraden Sechsecks mit gegebenen Eckpunkten

1. Listen Sie die x- und y-Koordinaten aller Scheitelpunkte auf. Wenn Sie die Eckpunkte des Sechsecks kennen, erstellen Sie als erstes eine Tabelle mit zwei Spalten und sieben Zeilen. Jede Zeile ist nach den sechs Punkten benannt (Punkt A, Punkt B, Punkt C usw.) und jede Spalte ist nach den x- oder y-Koordinaten dieser Punkte benannt. Listen Sie die x- und y-Koordinaten von Punkt A bis Punkt F auf. Wiederholen Sie die Koordinaten von Punkt A am Ende der Liste. Nehmen wir das folgende Beispiel mit dem Format Name:(x,y):
- A: (4, 10)
- B: (9, 7)
- K: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (wieder): (4, 10)

2. Multiplizieren Sie die x-Koordinate jedes Punktes mit der y-Koordinate des nächsten Punktes. Platziere die Ergebnisse rechts neben der Tabelle. Dann addiere die Ergebnisse zusammen.

3. Multiplizieren Sie die y-Koordinate jedes Punktes mit der x-Koordinate des nächsten Punktes. Füge die Ergebnisse zusammen.

4. Subtrahiere die zweite Summe von der ersten Summe. Subtrahiere 221 von 125. 125 - 221 = -96. Nehmen Sie nun den absoluten Wert dieser Antwort: 96. Bereich kann nur positiv sein.

5. Dividiere die berechnete Differenz durch zwei. Das Teilen von 96 durch 2 ergibt die Fläche des unregelmäßigen Sechsecks. 96/2 = 48. Denken Sie daran, dass die Einheit Ihrer Antwort der Quadratmeter ist. Die Antwort auf die Frage lautet daher 48 m.
Methode 4 von 4: Andere Methoden zur Berechnung der Fläche eines Hexagons

1. Finden der Fläche eines Sechsecks, in der ein Scheitelpunkt unbekannt ist. Wenn Sie wissen, dass Sie es mit einem regelmäßigen Sechseck mit fehlenden Dreiecken zu tun haben, berechnen Sie zunächst die Fläche, als ob das Sechseck vollständig wäre. Berechnen Sie dann einfach die Fläche der Dreiecke, die durch die Scheitelpunkte gebildet werden, und ziehen Sie sie von der Gesamtfläche ab. Dies gibt die Fläche des unregelmäßigen Sechsecks zurück.
- Ein Beispiel: Wenn Sie berechnet haben, dass die Fläche des regelmäßigen Sechsecks 60 cm beträgt und Sie wissen, dass die Fläche der fehlenden Dreiecke 10 cm beträgt, dann beträgt die Fläche des unregelmäßigen Sechsecks: 60 cm - 10 cm = 50 cm².
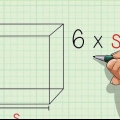
- Wenn Sie wissen, dass dem Sechseck genau ein Dreieck fehlt, ist es auch möglich, die Fläche des unregelmäßigen Sechsecks zu ermitteln, indem Sie die Fläche des regelmäßigen Sechsecks oder die Gesamtfläche mit 5/6 multiplizieren, da das unregelmäßige Sechseck einnimmt eine Fläche, die aus 5 der 6 Dreiecke des regelmäßigen Sechsecks besteht. Wenn zwei fehlen, multiplizieren Sie mit 4/6 usw.

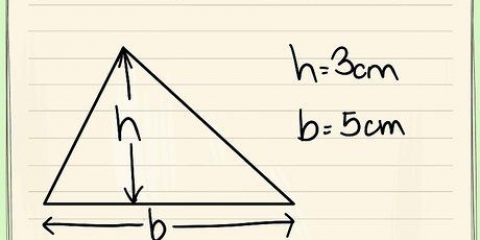
2. Brechen Sie ein unregelmäßiges Sechseck in andere Dreiecke. Es kann sein, dass das unregelmäßige Sechseck aus vier Dreiecken ungleicher Form besteht. Um die gesamte Fläche dieses Sechsecks zu finden, müssen Sie die Fläche jedes einzelnen Dreiecks ermitteln und dann zusammenzählen. Es gibt mehrere Möglichkeiten, die Fläche eines Dreiecks zu finden, je nachdem, was Sie wissen.

3. Suchen Sie nach anderen Formen im unregelmäßigen Sechseck. Wenn Sie keine Dreiecke finden können, sehen Sie nach, ob Sie andere Formen finden können - vielleicht ein Quadrat oder ein Rechteck. Sobald Sie die anderen Formen entdeckt haben, addieren Sie die Flächen, um die des gesamten Sechsecks zu berechnen.
"Berechnen sie die fläche eines sechsecks"
Оцените, пожалуйста статью