Das Apothem eines Sechsecks berechnen

Schritte
- Methode 1 von 2: Verwenden des Satzes des Pythagoras (Radiuslänge ist gegeben)
- Methode 2 von 2: Verwenden von Trigonometrie (und einem bestimmten Radius)
Tipps

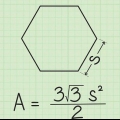
Ein Sechseck ist ein Vieleck mit sechs Winkeln und Seiten. Wenn ein Sechseck regelmäßig ist, hat es sechs gleiche Seiten und ein Apothem. Ein Apothem ist ein Liniensegment von der Mitte eines Polygons zur Mitte jeder Seite. Normalerweise muss die Länge des Apothems angegeben werden, um die Fläche eines Sechsecks zu berechnen. Solange Sie die Länge der Seite des Sechsecks kennen, können Sie die Länge des Apothems berechnen.

Schritte

Methode 1 von 2: Verwenden des Satzes des Pythagoras (Radiuslänge ist gegeben)

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 1

1. Teilen Sie das Sechseck in sechs kongruente gleichseitige Dreiecke. Zeichnen Sie dazu eine Linie von jedem Scheitelpunkt oder Punkt zum gegenüberliegenden Scheitelpunkt.

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 2

2. Wähle ein Dreieck und schreibe die Länge der Basis auf. Es ist gleich der Seitenlänge des Sechsecks.

Sie haben zum Beispiel ein Sechseck mit einer Länge von 8 cm für die Seite. Die Basis jedes gleichseitigen Dreiecks ist daher 8 cm.

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 3

3. Machen Sie zwei rechtwinklige Dreiecke. Sie tun dies, indem Sie eine Linie vom oberen Scheitelpunkt des gleichseitigen Dreiecks senkrecht zur Basis ziehen. Diese Linie halbiert die Basis des Dreiecks (also das Apothem des Sechsecks). Beschriften Sie die Länge der Basis eines der rechtwinkligen Dreiecke.

Wenn beispielsweise die Basis des gleichseitigen Dreiecks 8 cm beträgt, beträgt die Basis jedes rechtwinkligen Dreiecks – wenn Sie das Dreieck in zwei rechtwinklige Dreiecke teilen – jetzt 4 cm.

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 4

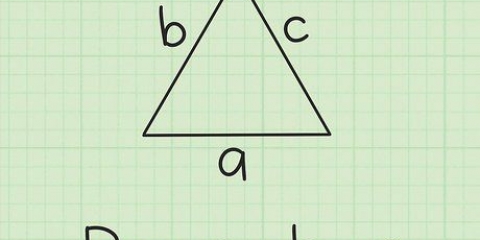
4. Verwenden Sie den Satz des Pythagoras. Die Formel lautet

ein 2 + B^{2} = C^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , wodurch

C

$C$ gleich der Länge der Hypotenuse (der Seite gegenüber dem rechten Winkel) und

ein

$ein$ und

B

$B$ gleich den Längen der anderen beiden Seiten des Dreiecks sein.

Wenn beispielsweise das rechtwinklige Dreieck eine Hypotenuse von hat

2

$2$ eine Seite von

1

$1$ und eine andere Seite von ungefähr

1, 732

$1.732$ (

\sqrt{3}

${sqrt{3}}$ ), dann besagt der Satz des Pythagoras, dass

12 + {\sqrt{3}}^{2} = 2^{2}

$1^{{2}}+{sqrt{3}}^{{2}}=2^{{2}}$ , was richtig ist, wenn du das herausfindest:

1 + 3 = 4

$1+3=4$ .

Bild mit dem Titel Berechnen Sie das Apothem eines Sechsecks Schritt 5

5. Setze die Länge der Basis des rechtwinkligen Dreiecks in die Formel ein. Ersatz für

B

$B$ .

Wenn die Länge der Basis beispielsweise 4 beträgt, würde Ihre Formel wie folgt aussehen:

ein 2 + 4^{2} = C^{2}

$a^{{2}}+4^{{2}}=c^{{2}}$ .

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 6

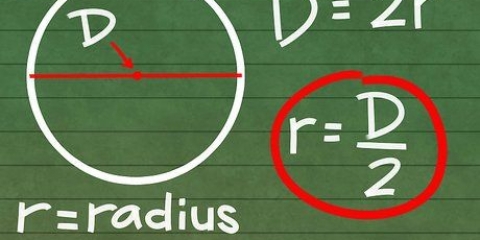
6. Setze die Länge der Hypotenuse in die Formel ein. Du kennst die Länge der Hypotenuse, weil du die Länge des Sechsecks kennst. Die Seitenlänge eines regelmäßigen Sechsecks ist gleich dem Radius des Sechsecks. Der Radius ist eine Linie, die den Mittelpunkt eines Polygons mit einem seiner Eckpunkte verbindet. Sie werden sehen, dass die Hypotenuse des rechtwinkligen Dreiecks auch der Radius des Sechsecks ist, also ist die Seitenlänge des Sechsecks gleich der Länge der Hypotenuse.

Wenn beispielsweise die Seitenlänge des Sechsecks 8 cm beträgt, beträgt die Länge der Hypotenuse des rechtwinkligen Dreiecks auch 8 cm. Ihre Formel sieht nun also so aus:

ein 2 + 4^{2} = 8^{2}

$a^{{2}}+4^{{2}}=8^{{2}}$ .

Bild mit dem Titel Berechnen Sie das Apothem eines Sechsecks Schritt 7

7. Quadrieren Sie die bekannten Werte der Formel. Denken Sie daran, dass das Quadrieren einer Zahl gleichbedeutend ist mit der Multiplikation dieser Zahl mit sich selbst.

Nach dem Quadrieren der bekannten Werte sieht Ihre Formel beispielsweise so aus:

ein 2 + 16 = 64

$a^{{2}}+16=64$ .

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 8

8. Isolieren Sie die unbekannte Variable. Sie tun dies, indem Sie den quadrierten Wert subtrahieren

B

$B$ von beiden Seiten der Gleichung.

Zum Beispiel:

ein 2 + 16 - 16 = 64 - 16

$a^{{2}}+16-16=64-16$

ein 2 = 48

$a^{{2}}=48$

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 9

9. Lösen für ein{displaystyle a} $ein$ . Sie tun dies, indem Sie die Quadratwurzel jeder Seite der Gleichung bestimmen. Dadurch erhalten Sie die Länge der fehlenden Seite des Dreiecks, die der Länge des Apothems des Sechsecks entspricht.

Mit einem Taschenrechner berechnen Sie beispielsweise

\sqrt{48} = 6, 93

${sqrt{48}}=6,93$ . Die fehlende Länge des rechtwinkligen Dreiecks und damit die Länge des Apothems des Sechsecks beträgt also 6,93 cm.

Methode 2 von 2: Verwenden von Trigonometrie (und einem bestimmten Radius)

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 10

1. Schreiben Sie die Formel, um das Apothem eines regelmäßigen Vielecks zu finden. Die Formel lautet

Apothema = S 2 bräunen (\frac{180}{n})

${text{apothema}}={frac{s}{2tan({frac{180}{n}})}}$ , wodurch

S

$S$ gleich der Seitenlänge des Polygons ist und

n

$n$ gleich der Anzahl der Seiten des Polygons.

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 11

2. Ersetzen Sie die Länge der Seite in der Formel. Vergessen Sie nicht, die Variable zu ersetzen

S

$S$ .

Für ein Sechseck mit einer Seitenlänge von 8 cm würde die Formel beispielsweise so aussehen:

8 2 bräunen (\frac{180}{n})

${frac{8}{2tan({frac{180}{n}})}}$ .

Bildtitel Berechnen Sie das Apothem eines Hexagons Schritt 12

3. Geben Sie die Anzahl der Seiten in die Formel ein. Ein Sechseck hat 6 Seiten. Vergessen Sie nicht, die Variable zu ersetzen

n

$n$ .

Zum Beispiel:

8 2 bräunen (\frac{180}{6})

${frac{8}{2tan({frac{180}{6}})}}$ .

Bildtitel Berechnen Sie das Apothem eines Sechsecks Schritt 13

4. Runden Sie die Berechnung in Klammern. Dies gibt Ihnen die Gradzahl, die Sie benötigen, um die Tangente zu berechnen.

Zum Beispiel,

\frac{180}{6} = 30

${frac{180}{6}}=30$ , womit die Formel nun so aussieht:

8 2 bräunen (30)

${frac{8}{2tan(30)}}$ .

Bild mit dem Titel Berechnen Sie das Apothem eines Sechsecks Schritt 14

5. Bestimmen Sie die Tangente. Verwenden Sie dazu einen Taschenrechner oder eine trigonometrische Tabelle.

Der Tangens von 30 beträgt beispielsweise etwa 0,577, die Formel würde also so aussehen:

8 2 (0, 577)

${frac{8}{2(0.577)}}$ .

Bildtitel Berechnen Sie das Apothem eines Hexagons Schritt 15

6. Multiplizieren Sie die Tangente mit 2 und teilen Sie dann die Länge einer Seite durch diese Zahl. Damit hast du die Länge des Apothems deines Sechsecks berechnet.

Zum Beispiel:

Apothema = 8 2 (0, 577)

${text{apothema}}={frac{8}{2(0,577)}}$

Apothema = 8 1, 154

${text{Apothema}}={frac{8}{1.154}}$

Apothema = 6, 93

${text{Apothema}}=6.93$
Das Apothem eines regelmäßigen Sechsecks mit Seitenlänge 8 cm beträgt also etwa 6,93 cm.

Tipps

Der Begriff `Apothem` kann sich auf das eigentliche Liniensegment oder auf die Länge dieses Liniensegments beziehen.
Denken Sie daran, dass diese Methode nur mit regelmäßigen Sechsecken funktioniert. Unregelmäßige Sechsecke haben kein Apothem.