Kostenlose Schritt für Schritt Anweisungen 
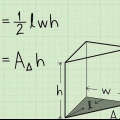
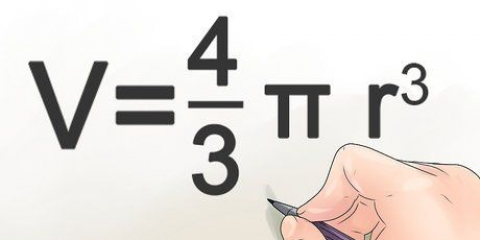Sie sind gerade der einfachen Formel zur Bestimmung des Volumens eines Dreiecksprismas gefolgt: 1/2 x BH x l.
Berechnung des volumens eines dreieckigen prismas
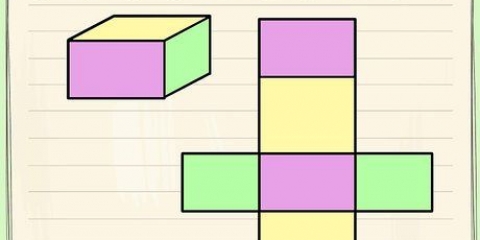
In der Geometrie verstehen wir unter einem dreieckigen Prisma ein dreiseitiges Polyeder mit zwei parallelen dreieckigen Grundflächen und drei rechteckigen Seiten, nicht zu verwechseln mit einer Pyramide. Um das Volumen eines dreieckigen Prismas zu berechnen, müssen Sie zuerst die Fläche einer Basis bestimmen und mit der Höhe des Prismas multiplizieren. In diesem Artikel können Sie lesen, wie das geht.
Schritte
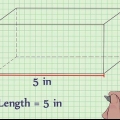
1. Finden Sie die Basis und Höhe einer der dreieckigen Basen. Die dreieckigen Basen des Dreiecksprismas sind gleich groß, es spielt also keine Rolle, welches Dreieck Sie verwenden. Bestimmen Sie nun die Basis und die Höhe des Dreiecks, indem Sie die Länge einer der Seiten des Dreiecks bestimmen. Bestimmen Sie die Höhe des Dreiecks, indem Sie die Länge einer Linie senkrecht zu dieser Basis bestimmen. Wenn Sie mit einem rechtwinkligen Dreieck arbeiten, nehmen Sie einfach die Längen der beiden Seiten, die senkrecht aufeinander stehen.
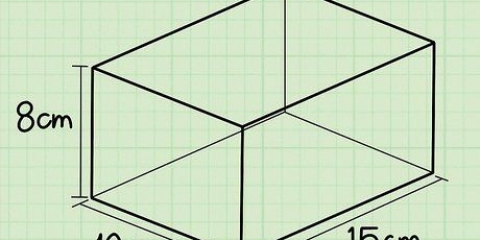
- Angenommen, wir haben ein Dreieck mit einer Höhe von 3 cm und einer Grundfläche von 4 cm.
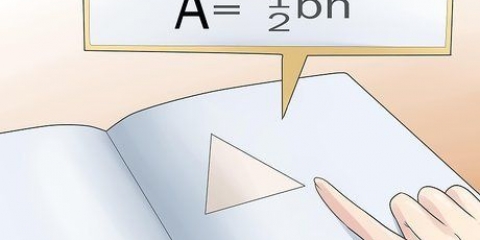
2. Multiplizieren Sie die Länge der Basis mit der Höhe. Das ist der erste Schritt, um die Fläche der Basis zu bestimmen; im Fall eines dreieckigen Prismas ist das ein Dreieck. Also: 3 cm x 4 cm = 12 cm. Vergessen Sie nicht, das Ergebnis in Quadratzentimetern anzugeben, da Sie mit Fläche arbeiten.
3. Teile das Ergebnis durch zwei. Um die Fläche dieser dreieckigen Basis zu finden, teilen Sie 12 cm durch 2. Also: 12 cm/2 = 6 cm.
4. Multiplizieren Sie diese Zahl mit der Höhe des Polyeders. Angenommen, die Höhe des dreieckigen Prismas oder die Länge einer seiner Seiten beträgt 10 cm. Dann multiplizieren wir 6 cm mit 10 cm, um das Volumen des dreieckigen Prismas zu finden. 6cm x 10cm = 60cm. Vergessen Sie nicht, das Ergebnis in Kubikeinheiten zu schreiben; du arbeitest mit inhalten.
Tipps
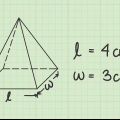
- Mit allen normal Pyramiden sind die Diagonale der Grundfläche, die Rippen und die Höhe, die nach dem Satz des Pythagoras miteinander verbunden sind: (Diagonale der Grundfläche/2)+ (Höhe)= (Länge der Rippe).
"Berechnung des volumens eines dreieckigen prismas"
Оцените, пожалуйста статью
