Zum Beispiel, wenn das Volumen des Prismas 64 . beträgt  ), sieht deine Formel so aus:
), sieht deine Formel so aus:


Wenn die Basis beispielsweise ein Rechteck von 8 Metern Länge und 2 Metern Breite ist, würden Sie die Fläche wie folgt berechnen:



Wenn Sie beispielsweise berechnet haben, dass die Fläche der Basis 16 m beträgt, sieht Ihre Formel so aus:


Zum Beispiel in der Gleichung  , du musst jede Seite durch 16 om teilen
, du musst jede Seite durch 16 om teilen  berechnen. Daher:
berechnen. Daher:


Die Höhe des rechteckigen Prismas beträgt also 4 Meter. 

Wenn Sie beispielsweise wissen, dass das Volumen des Prismas 840 Kubikmeter beträgt ( ), sieht deine Formel so aus:
), sieht deine Formel so aus:


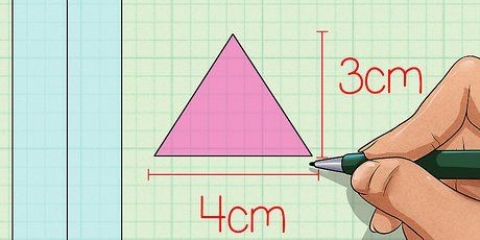
Wenn Sie die Länge aller drei Seiten eines Dreiecks kennen, können Sie die Fläche mit der Reiherformel berechnen.lesen Berechnen Sie die Fläche eines Dreiecks für detaillierte Anweisungen. Wenn die Basis des Dreiecks beispielsweise 12 Meter beträgt und die Höhe des Dreiecks 7 Meter beträgt, ermitteln Sie die Fläche wie folgt:




Wenn Sie beispielsweise wissen, dass die Grundfläche 42 m2 beträgt, sieht Ihre Formel so aus:


Zum Beispiel in der Gleichung  , Sie müssen jede Seite durch 42 teilen, um zu bestimmen
, Sie müssen jede Seite durch 42 teilen, um zu bestimmen  . Daher:
. Daher:


Die Höhe Ihres Dreiecksprismas beträgt also 20 Meter. 

Wenn die Fläche beispielsweise 1460 cm beträgt, würde Ihre Formel wie folgt aussehen:


Wenn die Basis beispielsweise ein Rechteck mit einer Länge von 8 cm und einer Breite von 2 cm ist, ermitteln Sie die Fläche wie folgt:



Wenn die Fläche der Basis beispielsweise 16 beträgt, würde Ihre Formel so aussehen:



Denken Sie daran, dass die gegenüberliegenden Seiten eines Rechtecks die gleiche Länge haben. Wenn die Basis beispielsweise ein Rechteck mit einer Länge von 8 cm und einer Breite von 2 cm ist, ermitteln Sie den Umfang wie folgt:



Wenn der Umfang der Basis beispielsweise 20 beträgt, würde Ihre Formel wie folgt aussehen:


Zum Beispiel in der Gleichung  Subtrahiere zuerst 32 von jeder Seite, dann dividiere jede Seite durch 20. Daher:
Subtrahiere zuerst 32 von jeder Seite, dann dividiere jede Seite durch 20. Daher:




Die Höhe Ihres Prismas beträgt also 71,4 cm. 

Wenn die Fläche beispielsweise 1460 cm beträgt, würde Ihre Formel wie folgt aussehen:


Wenn Sie die Länge aller drei Seiten eines Dreiecks kennen, können Sie die Fläche mit der Heron-Formel bestimmen.lesen Berechnen Sie die Fläche eines Dreiecks für vollständige Anweisungen. Wenn die Basis des Dreiecks beispielsweise 8 cm beträgt und die Höhe des Dreiecks 4 cm beträgt, würden Sie die Fläche wie folgt berechnen:




Wenn die Fläche der Basis beispielsweise 16 beträgt, würde Ihre Formel so aussehen:



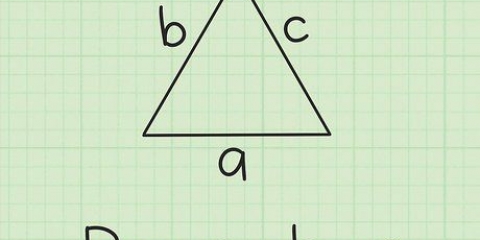
Wenn die Basis beispielsweise ein Dreieck mit den Längen 8, 4 und 9 cm ist, berechnen Sie den Umfang wie folgt:



Angenommen, der Umfang der Basis beträgt 21, Ihre Formel sieht wie folgt aus:


Zum Beispiel in der Gleichung  , Sie müssen zuerst 32 von jeder Seite subtrahieren und dann jede Seite durch 21 dividieren. Daher:
, Sie müssen zuerst 32 von jeder Seite subtrahieren und dann jede Seite durch 21 dividieren. Daher:




Die Höhe Ihres Prismas beträgt also 68 cm.
Berechnung der höhe eines prismas
- Schritte
- Methode 1 von 4: Ermitteln der Höhe eines rechteckigen Prismas mit bekanntem Volumen
- Methode 2 von 4: Bestimmung der Höhe eines dreieckigen Prismas mit bekanntem Volumen
- Methode 3 von 4: Ermitteln der Höhe eines rechteckigen Prismas anhand seiner Fläche
- Methode 4 von 4: Bestimmen Sie die Höhe eines Dreiecksprismas anhand seiner Fläche
- Notwendigkeiten
Ein Prisma ist eine dreidimensionale Figur mit zwei parallelen Basen, die deckungsgleich sind.Die Form der Basis bestimmt, um welche Art von Prisma es sich handelt, z. B. ein rechteckiges oder dreieckiges Prisma. Da es sich um eine 3D-Form handelt, ist es nicht ungewöhnlich, das Volumen eines Prismas berechnen zu wollen; dafür brauchst du allerdings die Höhe des Prismas. Das Ermitteln der Höhe ist möglich, wenn Sie genügend Informationen erhalten haben: entweder das Volumen, die Fläche und den Umfang der Basis. Die in den folgenden Methoden beschriebenen Formeln eignen sich für Prismen mit beliebig geformten Basen, vorausgesetzt, Sie kennen die Formel zum Ermitteln der Fläche dieser Form.
Schritte
Methode 1 von 4: Ermitteln der Höhe eines rechteckigen Prismas mit bekanntem Volumen

1. Verwenden Sie die Formel für das Volumen eines Prismas. Das Volumen eines Prismas kann mit der Formel ermittelt werden  , wodurch
, wodurch  gleich dem Volumen des Prismas,
gleich dem Volumen des Prismas,  gleich der Fläche einer Basis ist und
gleich der Fläche einer Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas.
 , wodurch
, wodurch  gleich dem Volumen des Prismas,
gleich dem Volumen des Prismas,  gleich der Fläche einer Basis ist und
gleich der Fläche einer Basis ist und  gleich der Höhe des Prismas.
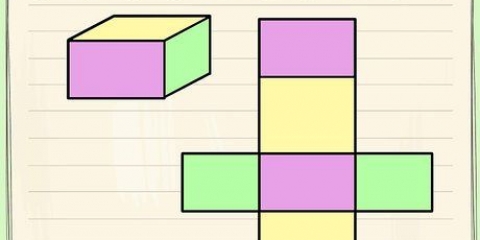
gleich der Höhe des Prismas. - Die Basis eines Prismas ist eine seiner kongruenten Seiten. Da alle gegenüberliegenden Seiten eines rechteckigen Prismas deckungsgleich sind, kann jede Seite als Grundebene verwendet werden, solange Sie mit Ihren Berechnungen konsistent sind.

2. Wende das Volumen auf die Formel an. Wenn Sie die Lautstärke nicht kennen, können Sie diese Methode nicht verwenden.
 ), sieht deine Formel so aus:
), sieht deine Formel so aus:

3. Finden Sie die Fläche der Basis. Um die Fläche zu finden, müssen Sie die Länge und Breite der Grundfläche (oder einer Seite, wenn die Grundfläche ein Quadrat ist) kennen. Verwenden Sie die Formel  um die Fläche eines Rechtecks zu bestimmen.
um die Fläche eines Rechtecks zu bestimmen.
 um die Fläche eines Rechtecks zu bestimmen.
um die Fläche eines Rechtecks zu bestimmen.


4. Ersetze die Fläche der Basis in das Volumen der Prismenformel. Stellen Sie sicher, dass Sie die Variable ersetzen  .
.
 .
.

5. Löse die Gleichung nach h  . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas.
 . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas. , du musst jede Seite durch 16 om teilen
, du musst jede Seite durch 16 om teilen  berechnen. Daher:
berechnen. Daher:

Die Höhe des rechteckigen Prismas beträgt also 4 Meter.
Methode 2 von 4: Bestimmung der Höhe eines dreieckigen Prismas mit bekanntem Volumen

1. Schreiben Sie die Formel für das Volumen eines Prismas auf. Das Volumen jedes Prismas kann mit der Formel ermittelt werden  ,wodurch
,wodurch  gleich dem Volumen des Prismas,
gleich dem Volumen des Prismas,  gleich der Fläche einer Basis ist und
gleich der Fläche einer Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas.
 ,wodurch
,wodurch  gleich dem Volumen des Prismas,
gleich dem Volumen des Prismas,  gleich der Fläche einer Basis ist und
gleich der Fläche einer Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas. - Die Basis eines Prismas ist eine seiner kongruenten Seiten. Die Basis eines dreieckigen Prismas ist ein Dreieck. Die Seiten sind Rechtecke.

2. Wende das Volumen auf die Formel an. Wenn Sie die Lautstärke nicht kennen, können Sie diese Methode nicht verwenden.
 ), sieht deine Formel so aus:
), sieht deine Formel so aus:

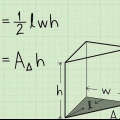
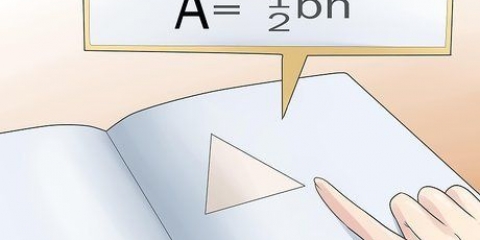
3. Finden Sie die Fläche der Basis. Um die Fläche zu finden, müssen Sie die Länge der Basis des Dreiecks und die Höhe des Dreiecks kennen. Verwenden Sie die Formel  zur Bestimmung der Fläche eines Dreiecks.
zur Bestimmung der Fläche eines Dreiecks.
 zur Bestimmung der Fläche eines Dreiecks.
zur Bestimmung der Fläche eines Dreiecks.



4. Ersetze die Fläche der Basis in das Volumen der Prismenformel. Stellen Sie sicher, dass Sie die Variable ersetzen  .
.
 .
.

5. Löse die Gleichung nach h  . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas.
 . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas. , Sie müssen jede Seite durch 42 teilen, um zu bestimmen
, Sie müssen jede Seite durch 42 teilen, um zu bestimmen  . Daher:
. Daher:

Methode 3 von 4: Ermitteln der Höhe eines rechteckigen Prismas anhand seiner Fläche

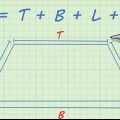
1. Schreiben Sie die Formel für die Fläche eines Prismas. Die Formel für die Fläche eines Prismas lautet  , wodurch
, wodurch  ist gleich der Oberfläche,
ist gleich der Oberfläche,  ist gleich der Fläche der Basis,
ist gleich der Fläche der Basis,  gleich dem Umfang der Basis ist und
gleich dem Umfang der Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas.
 , wodurch
, wodurch  ist gleich der Oberfläche,
ist gleich der Oberfläche,  ist gleich der Fläche der Basis,
ist gleich der Fläche der Basis,  gleich dem Umfang der Basis ist und
gleich dem Umfang der Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas. - Damit diese Methode funktioniert, müssen Sie die Fläche des Prismas sowie die Länge und Breite der Basis kennen.

2. Ersetzen Sie die Fläche des Prismas in der Formel. Wenn die Oberfläche unbekannt ist, funktioniert diese Methode nicht.


3. Finden Sie die Fläche der Basis. Um die Fläche zu finden, müssen Sie die Länge und Breite der Basis kennen (oder eine Seite, wenn die Basis ein Quadrat ist). Verwenden Sie die Formel  um die Fläche eines Rechtecks zu bestimmen.
um die Fläche eines Rechtecks zu bestimmen.
 um die Fläche eines Rechtecks zu bestimmen.
um die Fläche eines Rechtecks zu bestimmen.


4. Ersetzen Sie die Fläche der Basis in der Formel durch die Fläche eines Prismas und vereinfachen Sie. Stellen Sie sicher, dass Sie den Brief ausfüllen  .
.
 .
.


5. Bestimmen Sie den Umfang der Basis. Um den Umfang eines Rechtecks zu ermitteln, addieren Sie die Längen aller vier Seiten zusammen oder multiplizieren Sie die Länge einer Seite mit 4, wenn es sich um ein Quadrat handelt.



6. Ersetzen Sie den Umfang der Basis in der Formel für die Fläche eines Prismas. Stellen Sie sicher, dass Sie den Buchstaben ersetzen  .
.
 .
.

7. Löse die Gleichung nach h  . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas.
 . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas. Subtrahiere zuerst 32 von jeder Seite, dann dividiere jede Seite durch 20. Daher:
Subtrahiere zuerst 32 von jeder Seite, dann dividiere jede Seite durch 20. Daher:



Methode 4 von 4: Bestimmen Sie die Höhe eines Dreiecksprismas anhand seiner Fläche

1. Schreiben Sie die Formel für die Fläche eines Prismas. Die Formel für die Fläche eines Prismas lautet  , wodurch
, wodurch  ist gleich der Oberfläche,
ist gleich der Oberfläche,  ist gleich der Fläche der Basis,
ist gleich der Fläche der Basis,  gleich dem Umfang der Basis ist und
gleich dem Umfang der Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas.
 , wodurch
, wodurch  ist gleich der Oberfläche,
ist gleich der Oberfläche,  ist gleich der Fläche der Basis,
ist gleich der Fläche der Basis,  gleich dem Umfang der Basis ist und
gleich dem Umfang der Basis ist und  gleich der Höhe des Prismas.
gleich der Höhe des Prismas. - Damit diese Methode funktioniert, muss die Fläche des Prismas sowie die Fläche der dreieckigen Basis und die Länge aller drei Seiten der Basis bekannt sein.

2. Ersetzen Sie die Fläche des Prismas in der Formel. Wenn die Oberfläche nicht bekannt ist, funktioniert diese Methode nicht.


3. Finden Sie die Fläche der Basis. Um die Fläche zu finden, müssen Sie die Länge der Basis des Dreiecks und die Höhe des Dreiecks kennen. Verwenden Sie die Formel  zur Bestimmung der Fläche eines Dreiecks.
zur Bestimmung der Fläche eines Dreiecks.
 zur Bestimmung der Fläche eines Dreiecks.
zur Bestimmung der Fläche eines Dreiecks.



4. Ersetzen Sie die Fläche der Basis in der Formel für die Fläche eines Prismas und vereinfachen Sie. Ersatz für  .
.
 .
.


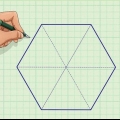
5. Bestimmen Sie den Umfang der Basis. Um den Umfang eines Dreiecks zu ermitteln, addieren Sie die Längen aller drei Seiten zusammen.



6. Ersetzen Sie den Umfang der Basis in der Formel für die Fläche eines Prismas. Stellen Sie sicher, dass Sie für ersetzen  .
.
 .
.

7. Löse die Gleichung nach h  . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas.
 . Jetzt kennen Sie die Höhe Ihres Prismas.
. Jetzt kennen Sie die Höhe Ihres Prismas. , Sie müssen zuerst 32 von jeder Seite subtrahieren und dann jede Seite durch 21 dividieren. Daher:
, Sie müssen zuerst 32 von jeder Seite subtrahieren und dann jede Seite durch 21 dividieren. Daher:



Notwendigkeiten
- Stift/Bleistift und Papier oder Taschenrechner (optional)
"Berechnung der höhe eines prismas"
Оцените, пожалуйста статью