Berechnen der fläche eines würfels
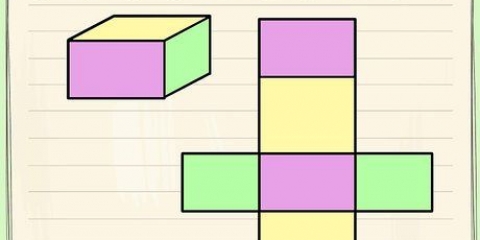
Die Fläche eines Objekts ist die kombinierte Fläche all seiner Seiten. Alle sechs Seiten eines Würfels sind deckungsgleich. Um also die Fläche eines Würfels zu finden, müssen Sie nur die Fläche einer Seite des Würfels kennen und diese dann mit sechs multiplizieren. Wenn Sie wissen möchten, wie Sie die Fläche eines Würfels berechnen, folgen Sie diesen Schritten.
Schritte
Methode 1 von 2: Wenn die Fläche einer Seite bekannt ist

1. Verstehe, dass die Fläche eines Würfels die Summe der Fläche seiner sechs Seiten ist. Da alle Seiten eines Würfels deckungsgleich sind, können wir einfach die Fläche einer Seite ermitteln und mit sechs multiplizieren, um die Gesamtfläche zu erhalten. Die Fläche kann mit einer einfachen Formel ermittelt werden: 6 x s, wobei `s` eine Kante des Würfels darstellt.

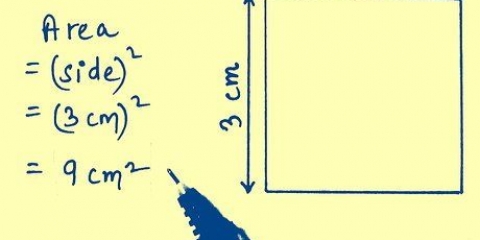
2. Finden Sie die Fläche einer Seite des Würfels. Um die Fläche einer Seite des Würfels zu ermitteln, müssen Sie `s` finden, das die Länge einer Kante eines Würfels darstellt, und dann s . berechnen. Dies bedeutet, dass Sie die Länge der Würfelseite mit seiner Breite multiplizieren, um seine Fläche zu ermitteln – die Länge und Breite der Würfelseite sind gleich. Wenn eine Seite des Würfels `s` 4 cm beträgt, beträgt die Fläche der Seite des Würfels (4 cm) oder 16 cm. Vergessen Sie nicht, Ihre Antwort in Quadrateinheiten anzugeben.

3. Multiplizieren Sie die Fläche der Seite des Würfels mit sechs. Nachdem Sie nun die Fläche einer Seite des Würfels gefunden haben, können Sie die Fläche des Würfels bestimmen, indem Sie diese Zahl mit sechs multiplizieren. 16cm x 6 = 96cm. Die Oberfläche des Würfels beträgt 96 cm².
Methode 2 von 2: Wenn das Volumen bekannt ist

1. Finde das Volumen des Würfels. Nehmen wir an, das Volumen des Würfels beträgt 125 cm.

2. Finde die Kubikwurzel des Volumens. Um die Kubikwurzel des Volumens zu finden, suchen Sie nach einer Zahl, die in die Kubik des Volumens erhöht werden kann, oder verwenden Sie einen Taschenrechner. Die Zahl wird nicht immer eine ganze Zahl sein. In diesem Fall ist die Zahl 125 ein perfekter Würfel und die Quadratwurzel des Würfels ist fünf, denn 5 x 5 x 5 x 5 x 5 = 125. `s` (eine Kante des Würfels) ist also fünf.

3. Wende diese Antwort auf die Formel für die Fläche eines Würfels an. Da Sie nun die Länge einer Seite eines Würfels kennen, geben Sie diese in die Formel zum Ermitteln der Fläche eines Würfels ein: 6 x s. Da die Länge einer Rippe 5 cm beträgt, lautet die vervollständigte Formel: 6 x (5 cm).

4. Lösen. Das ist nur ein bisschen Mathe. 6 x (5 cm) = 6 x 25 cm = 150 cm.
Оцените, пожалуйста статью