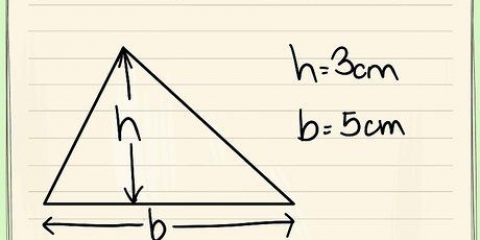
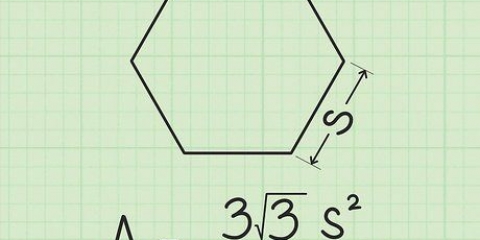
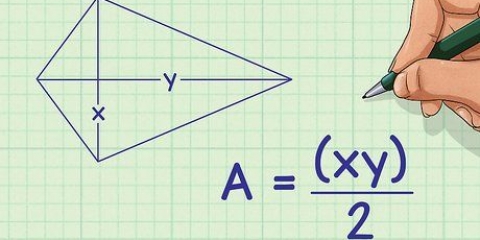In unserem Beispiel ist die Fläche des Dreiecks=½ x 3 x 2=3. 
In unserem Beispiel ist A(Summe des Fünfecks)=5 x A(Dreieck)=5 x 3=fünfzehn. 



Der Base des Dreiecks ist ½ mal die Seite des Fünfecks. In unserem Beispiel sind dies ½ x 7=3,5 Einheiten. Der Ecke in der Mitte des Fünfecks ist immer 36º. (Angenommen 360º für einen Vollkreis, können Sie diesen in 10 kleinere Dreiecke aufteilen. 360 ÷ 10=36, der Winkel eines solchen Dreiecks beträgt also 36º). 
In einem rechtwinkligen Dreieck ist die is Tangente eines Winkels gleich der Länge der gegenüberliegenden Seite geteilt durch die Länge der angrenzenden Seite. Die dem Winkel von 36° gegenüberliegende Seite ist die Basis des Dreiecks (die halbe Seite des Fünfecks). Die angrenzende Seite des Winkels von 36º ist die Höhe des Dreiecks. tan(36º)=entgegengesetzt / benachbart In unserem Beispiel ist tan(36º)=3,5 / Höhe Höhe x Bräune (36º) = 3.5 Höhe = 3,5 / tan (36º) Höhe = (ungefähr) 4.8. 
In unserem Beispiel beträgt die Fläche eines der kleinen Dreiecke=½bh=½(3.5)(4.8)=8.4. 
In unserem Beispiel ist die Fläche des gesamten Fünfecks = 8,4 x 10 =84. 

Fläche eines regelmäßigen Fünfecks=(5S ) / (4tan(36º)), wobei S=Länge einer Seite. tan(36º)=√(5-2√5). Wenn Ihr Taschenrechner keine `tan`-Funktion hat, verwenden Sie die Formel für die Fläche: Fläche=(5S) / (4√(5-2√5)). 
Die Fläche eines regelmäßigen Fünfecks=(5/2)RSünde(72º), wobei R der radius ist.
Berechnen sie die fläche eines fünfecks
Ein Fünfeck ist ein Vieleck mit fünf geraden Seiten. Fast alle Probleme, denen Sie im Mathematikunterricht begegnen werden, beinhalten regelmäßige Fünfecke mit fünf gleichen Seiten. Es gibt zwei gängige Methoden, um die Fläche zu berechnen, je nachdem, wie viele Informationen Sie haben.
Schritte
Methode 1 von 3: Bestimmen der Fläche anhand der Seiten und des Apothems

1. Beginnen Sie mit der Länge der Seite und einem Apothem. Diese Methode funktioniert für regelmäßige Fünfecke mit fünf gleichen Seiten. Zusätzlich zur Seitenlänge braucht man das `Apothema` des Fünfecks. Das Apothem ist die Linie von der Mitte des Fünfecks zu einer Seite, die die Seite senkrecht schneidet (d. h. in einem Winkel von 90º).
- Verwechseln Sie das Apothem nicht mit dem Radius eines Polygons, denn es schneidet einen Winkel (Scheitelpunkt) statt einen Punkt in der Mitte der Seite. Wenn Sie nur die Länge einer Seite und den Radius kennen, fahren Sie mit der nächsten Methode fort.
- Als Beispiel verwenden wir ein Fünfeck mit Seite 3 und apotheme 2.

2. Teilen Sie das Fünfeck in fünf Dreiecke. Zeichnen Sie fünf Linien von der Mitte des Fünfecks, die jeweils zu einem Scheitelpunkt (Ecke) führen. Du hast jetzt fünf Dreiecke.

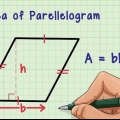
3. Berechnen Sie die Fläche eines Dreiecks. Jedes Dreieck hat a Base gleich der Seite des Fünfecks. Es hat auch eine Höhe was gleich dem apothem ist. (Denken Sie daran, die Höhe eines Dreiecks ist die Länge der Seite, die senkrecht zu seiner Basis steht und sich bis zu einem Scheitelpunkt erstreckt.). Um die Fläche eines Dreiecks zu berechnen, verwenden Sie ½ x Basis x Höhe.

4. Mit fünf multiplizieren für die Gesamtfläche des Fünfecks. Wir haben das Fünfeck in fünf gleiche Dreiecke unterteilt. Um die Gesamtfläche zu berechnen, multiplizieren Sie die Fläche eines Dreiecks mit fünf.
Methode 2 von 3: Bestimmen der Fläche anhand der Länge einer Seite

1. Beginnen Sie mit der Länge einer Seite. Diese Methode funktioniert nur bei regelmäßigen Fünfecken, die fünf gleich lange Seiten haben.
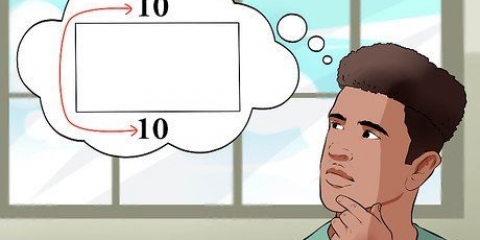
- In diesem Beispiel verwenden wir ein Fünfeck mit der Länge 7 für jede Seite.

2. Teilen Sie das Fünfeck in fünf Dreiecke. Zeichnen Sie eine Linie von der Mitte des Fünfecks zu einem Scheitelpunkt. Wiederholen Sie dies für jeden Scheitelpunkt. Sie haben jetzt fünf gleichgroße Dreiecke.

3. Teile ein Dreieck in zwei Hälften. Zeichnen Sie eine Linie von der Mitte des Fünfecks zur Basis eines Dreiecks. Diese Linie sollte die Basis im rechten Winkel (90º) schneiden, was das Dreieck in zwei gleiche, kleinere Dreiecke teilt.

4. Beschrifte eines der kleineren Dreiecke. Wir können bereits eine Seite und einen Winkel des kleineren Dreiecks benennen:

5. Berechnen Sie die Höhe des Dreiecks. Der Höhe dieses Dreiecks ist die Seite senkrecht zur Seite des Fünfecks, die zum Mittelpunkt führt. Wir verwenden einfache Trigonometrie, um die Länge dieser Seite zu bestimmen:

6.Berechnen Sie die Fläche des Dreiecks. Die Fläche eines Dreiecks ist gleich ½ Basis x Höhe. (A=½bh.) Nun, da Sie die Höhe kennen, geben Sie diese Werte ein, um die Höhe Ihres kleinen Dreiecks zu bestimmen.

7. Multiplizieren Sie, um die Fläche des Fünfecks zu finden. Eines dieser kleineren Dreiecke bedeckt 1/10 der Fläche des Fünfecks. Für die Gesamtfläche multiplizieren Sie die Fläche des kleineren Dreiecks mit 10.
Methode 3 von 3: Verwenden einer Formel

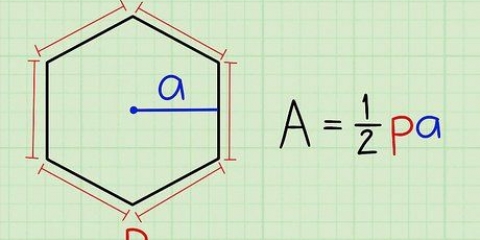
1. Verwenden Sie die Gliederung und das Apothem. Das Apothem ist eine Linie von der Mitte eines Fünfecks, die eine Seite im rechten Winkel schneidet. Wenn die Länge angegeben ist, können Sie diese einfache Formel verwenden.
- Fläche eines regelmäßigen Fünfecks=Vati / 2, wobei P=der Umfang und ein=das Apothem.
- Wenn Sie den Umfang nicht kennen, berechnen Sie ihn mit der Länge der Seite: p=5s, wobei s die Länge der Seite ist.

2. Nutze die Seitenlänge. Wenn Sie nur die Länge der Seiten kennen, verwenden Sie die folgende Formel:

3. Wählen Sie eine Formel, die nur den Radius verwendet. Du kannst sogar die Gegend finden, wenn du nur den Radius kennst. Verwenden Sie die folgende Formel:
Tipps
- Unregelmäßige Fünfecke oder Fünfecke mit ungleichen Seiten sind schwieriger zu studieren. Der beste Ansatz besteht normalerweise darin, das Fünfeck in Dreiecke zu unterteilen und die Flächen aller Dreiecke zusammenzuzählen. Möglicherweise müssen Sie auch eine größere Form um das Fünfeck zeichnen, seine Fläche berechnen und dann die Fläche des zusätzlichen Raums subtrahieren.
- Verwenden Sie nach Möglichkeit sowohl eine geometrische Methode als auch eine Formel und vergleichen Sie die Ergebnisse, um Ihre Antwort zu überprüfen. Die Antworten können sich leicht unterscheiden, wenn Sie die Formel in einem Rutsch vollständig ausfüllen (da dann die Schritte fehlen, in denen Sie ausfüllen), aber sie sollten sehr nahe beieinander liegen.
- Die hier angegebenen Beispiele verwenden gerundete Werte, um ihre Berechnung zu erleichtern. Wenn Sie ein echtes Polygon mit den angegebenen Seitenlängen haben, erhalten Sie für die anderen Längen und Flächen etwas andere Ergebnisse.
- Die Formeln sind aus geometrischen Methoden abgeleitet, ähnlich den hier beschriebenen. Versuchen Sie herauszufinden, wie Sie sie selbst ablenken können. Die Radiusformel ist schwieriger abzuleiten als die anderen (Hinweis: Sie benötigen die Doppelwinkelidentität).
"Berechnen sie die fläche eines fünfecks"
Оцените, пожалуйста статью