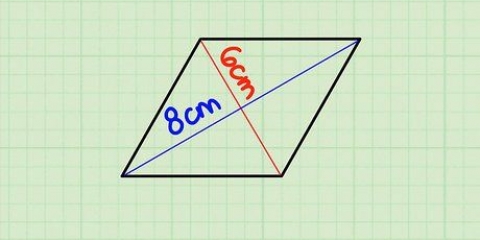
Wenn ein Drachen beispielsweise zwei Diagonalen von 7 cm und 10 cm hat, würde Ihre Formel so aussehen: .
. 
Zum Beispiel:



Zum Beispiel:


Die Fläche eines Drachens mit Diagonalen von 10 cm und 7 cm beträgt demnach 35 Quadratzentimeter. 

Wenn dein Kite beispielsweise eine Seite von 20 cm und eine Seite von 15 cm hat, sieht deine Formel wie folgt aus:  .
. 
Zum Beispiel:



Zum Beispiel: wenn der Winkel  dann sieht deine formel so aus:
dann sieht deine formel so aus:  .
. 
Der Sinus eines 150-Grad-Winkels beträgt beispielsweise 0,5, daher sieht Ihre Formel wie folgt aus:  .
. 
Zum Beispiel:


Die Fläche eines Drachens mit zwei Seiten von 20 cm und 15 cm und einem Winkel zwischen ihnen von 150 Grad beträgt also 150 Quadratzentimeter. 

Wenn Ihr Drachen beispielsweise eine Fläche von 35 cm² hat, sieht Ihre Formel so aus:  .
. 
Wenn Sie beispielsweise wissen, dass eine der Diagonalen 7 cm lang ist, sieht Ihre Formel so aus:  .
. 
Zum Beispiel:




Zum Beispiel:



Die Länge der fehlenden Diagonale eines Drachens beträgt bei einer Fläche von 35 cm² und einer Diagonale von 7 cm also 10 cm.
Berechnen sie die fläche eines drachens
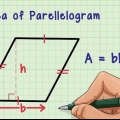
Ein Drachen ist eine Art Viereck mit zwei Paaren gleicher, benachbarter Seiten. Drachen können das traditionelle Aussehen eines Drachens haben, aber ein Drachen kann auch ein Diamant oder ein Quadrat sein. Egal wie ein Drachen aussieht, die Methoden zum Auffinden der Oberfläche sind die gleichen. Wenn Sie die Länge der Diagonalen kennen, können Sie die Fläche durch einfache Mathematik ermitteln. Sie können auch die Trigonometrie verwenden, um die Fläche zu finden, wenn Sie die Seiten und Winkel der Figur kennen.
Schritte
Methode 1 von 3: Verwenden der Diagonalen zur Bestimmung der Fläche

1. Schreibe die Formel für die Fläche eines Drachens, gegeben zwei Diagonalen. Die Formel lautet  , wodurch
, wodurch  ist gleich der Fläche des Drachens, und
ist gleich der Fläche des Drachens, und  und
und  entspricht der Länge der Drachendiagonalen.
entspricht der Länge der Drachendiagonalen.
 , wodurch
, wodurch  ist gleich der Fläche des Drachens, und
ist gleich der Fläche des Drachens, und  und
und  entspricht der Länge der Drachendiagonalen.
entspricht der Länge der Drachendiagonalen.
2. Wenden Sie die Längen der Diagonalen auf die Formel an. Eine Diagonale ist eine gerade Linie, die von einem Scheitelpunkt zum Scheitelpunkt auf der anderen Seite verläuft. Sie sollten entweder die Länge der Diagonalen erhalten oder in der Lage sein, sie zu messen. Wenn Sie die Länge der Diagonalen nicht kennen, können Sie diese Methode nicht verwenden.
 .
.
3. Multiplizieren Sie die Längen der Diagonalen. Das Produkt wird zur neuen Theke im Flächenvergleich.



4. Dividiere das Produkt der Diagonalen durch 2. Dadurch erhältst du die Fläche des Drachens in Quadrateinheiten.


Die Fläche eines Drachens mit Diagonalen von 10 cm und 7 cm beträgt demnach 35 Quadratzentimeter.
Methode 2 von 3: Verwenden eines Winkels und zweier Seiten zur Bestimmung der Fläche

1. Schreibe die Formel für die Oberfläche des Drachens. Diese Formel funktioniert, wenn Sie zwei nicht übereinstimmende Seiten und die Größe des Winkels zwischen diesen beiden Seiten kennen. Die Formel lautet  , wodurch
, wodurch  ist gleich der Fläche des Drachens,
ist gleich der Fläche des Drachens,  und
und  gleich den ungleichen Seiten des Drachens ist und
gleich den ungleichen Seiten des Drachens ist und  gleich Winkel zwischen den Seiten
gleich Winkel zwischen den Seiten und
und  .
.
 , wodurch
, wodurch  ist gleich der Fläche des Drachens,
ist gleich der Fläche des Drachens,  und
und  gleich den ungleichen Seiten des Drachens ist und
gleich den ungleichen Seiten des Drachens ist und  gleich Winkel zwischen den Seiten
gleich Winkel zwischen den Seiten und
und  .
. - Überprüfen Sie, ob Sie zwei ungleiche Seiten haben. Ein Drachen hat zwei Paare kongruenter Seiten. Sie müssen eine Seite jedes Paares verwenden. Stellen Sie sicher, dass Sie mit dem Winkel zwischen diesen beiden Seiten beginnen. Wenn Sie nicht über alle diese Informationen verfügen, können Sie diese Methode nicht verwenden.

2. Wenden Sie die Länge der Seiten auf die Formel an. Diese Angabe muss unbedingt gemacht werden, sonst muss man sie messen können. Denken Sie daran, dass Sie nicht deckungsgleiche Seiten verwenden, sodass jede Seite eine andere Länge hat.
 .
.
3. Multiplizieren Sie die Seiten zusammen. Wenden Sie dieses Produkt auf die Formel an.



4. Wende den Winkel auf die Formel an. Achten Sie darauf, den Winkel zwischen den beiden nicht deckungsgleichen Seiten zu verwenden.
 dann sieht deine formel so aus:
dann sieht deine formel so aus:  .
.
5. Bestimmen Sie den Sinus des Winkels. Dazu können Sie einen Taschenrechner oder eine trigonometrische Tabelle verwenden.
 .
.
6. Multiplizieren Sie das Produkt der Seiten mit dem Sinus des Winkels. Dieses Ergebnis ist die Fläche des Drachens, in Quadrateinheiten.


Die Fläche eines Drachens mit zwei Seiten von 20 cm und 15 cm und einem Winkel zwischen ihnen von 150 Grad beträgt also 150 Quadratzentimeter.
Methode 3 von 3: Verwenden der Fläche, um eine fehlende Diagonale zu finden

1. Schreibe die Formel für die Fläche eines Drachens, gegeben zwei Diagonalen. Die Formel lautet  , wodurch
, wodurch  ist gleich der Fläche des Drachens, und
ist gleich der Fläche des Drachens, und  und
und  entspricht der Länge der Drachendiagonalen.
entspricht der Länge der Drachendiagonalen.
 , wodurch
, wodurch  ist gleich der Fläche des Drachens, und
ist gleich der Fläche des Drachens, und  und
und  entspricht der Länge der Drachendiagonalen.
entspricht der Länge der Drachendiagonalen.
2. Wende die Fläche des Drachens auf die Formel an. Diese Informationen sollten gegeben werden. Stell sicher, dass du  ersetzt.
ersetzt.
 ersetzt.
ersetzt. .
.
3. wende die Länge der bekannten Diagonale auf die Formel an. ersetzen  .
.
 .
. .
.
4. Multiplizieren Sie jede Seite der Gleichung mit 2. Dadurch wird der Bruch in der Formel entfernt.




5. Teilen Sie jede Seite der Gleichung durch die Länge der Diagonalen. Dadurch erhalten Sie die Länge der fehlenden Diagonale.



Die Länge der fehlenden Diagonale eines Drachens beträgt bei einer Fläche von 35 cm² und einer Diagonale von 7 cm also 10 cm.
Notwendigkeiten
- Rechner (optional)
- Lineal (optional)
- Bleistift (optional)
- Papier (optional)
Оцените, пожалуйста статью