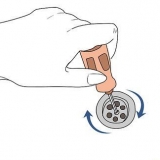
Verlegen Sie einen Faden um den Umfang, so genau wie möglich. Markieren Sie den Draht, wenn der Kreis vollständig ist, und messen Sie dann die Länge des Drahts mit einem Lineal. 




π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11 *12) - 4/(12*13*14) ... Sie wenden diese Formel an, indem Sie zuerst 2 nehmen und dann abwechselnd Brüche addieren und subtrahieren, wobei der Zähler 4 und der Nenner das Produkt von 3 aufeinanderfolgenden ganzen Zahlen sind, die mit jeder neuen Iteration wachsen. Jeder aufeinanderfolgende Bruch beginnt mit einer Reihe von ganzen Zahlen, wobei die erste Zahl der Reihe die letzte Zahl der vorherigen Reihe ist (im vorherigen Bruch). Auch wenn Sie dies nur ein paar Mal tun, werden Sie pi . bald nahe kommen. 


pi=2 *(Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x)). Arcsin bezieht sich auf einen inversen Sinus im Bogenmaß Sqrt ist eine Abkürzung für die Quadratwurzel von Abs ist eine Abkürzung für Absolutwert x^2 ist eine bestimmte Potenz, in diesem Fall x zum Quadrat.
Berechnen pi
Pi (π) ist eine der wichtigsten und faszinierendsten Zahlen der Mathematik. Einfach als 3 . angezeigt.14, wird als Konstante zur Berechnung des Umfangs eines Kreises verwendet, indem sein Radius oder Durchmesser verwendet wird. Es ist auch eine irrationale Zahl, was bedeutet, dass Sie sie auf unendlich viele Dezimalstellen berechnen können, ohne jemals auf ein sich wiederholendes Muster zu stoßen. Dies macht es schwierig, aber nicht unmöglich, genau zu arbeiten.
Schritte
Methode 1 von 5: Berechnen von Pi mit einem Kreis

1. Achte darauf, einen perfekten Kreis zu verwenden. Diese Methode funktioniert nicht mit einer Ellipse, Ellipse oder etwas anderem als einem echten Kreis. Ein Kreis ist definiert als alle Punkte in einer Ebene, die von einem bestimmten Mittelpunkt gleich weit entfernt sind. Zum Beispiel sind Deckel eines Marmeladenglases ein schönes Hilfsmittel für diese Übung. Damit kannst du grob einen Wert von Pi berechnen. Selbst der dünnste, spitzeste Bleistift ist noch enorm im Vergleich zur Genauigkeit, die für eine exakte Berechnung der Zahl Pi . erforderlich ist.

2. Messen Sie den Umfang des Kreises so genau wie möglich. Der Umfang ist die Länge des gesamten Umfangs des Kreises. Da dies rund läuft, kann es etwas schwierig zu messen sein (deshalb ist Pi so wichtig).

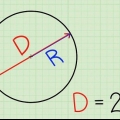
3. Messen Sie den Durchmesser des Kreises. Der Durchmesser ist die Länge des Querschnitts eines Kreises durch den Kreismittelpunkt.

4. Verwenden Sie die Formel. Der Umfang eines Kreises kann mit der Formel ermittelt werden C=π*d=2*π*r. Also ist pi gleich dem Umfang des Kreises geteilt durch den Durchmesser. Geben Sie Ihre Zahlen in einen Taschenrechner ein: Das Ergebnis sollte ungefähr 3 . betragen.sollte 14 . sein.

5. Um ein genaueres Ergebnis zu erhalten, wiederholen Sie diesen Vorgang für mehrere Kreise und mitteln Sie dann die Ergebnisse. Ihre Messwerte sind möglicherweise nicht perfekt, wenn es um eine individuelle Messung geht, aber im Laufe der Zeit sollte der Durchschnitt eine wirklich gute Annäherung an Pi . sein.
Methode 2 von 5: Berechnen von Pi mit unendlichen Reihen

1. Nutzen Sie die Gregory-Leibniz-Reihe. Mathematiker haben mehrere mathematische Folgen gefunden, die, wenn sie bis ins Unendliche verfolgt werden, Pi auf eine enorme Anzahl von Dezimalstellen berechnen können. Einige dieser Sequenzen sind so komplex, dass Supercomputer sie verarbeiten müssen. Eine der einfachsten ist jedoch die Gregory-Leibniz-Reihe. Vielleicht nicht sehr effizient, aber es erzeugt mit jeder Iteration eine genauere Zahl für pi, die schließlich bei 5 Dezimalstellen nach 500 endet.000 Iterationen. Hier ist die zu verwendende Formel.
- π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Nimm 4 und subtrahiere 4 geteilt durch 3 davon. Dann addiere 4 geteilt durch 5. Dann subtrahiere 4 geteilt durch 7 wieder. Wiederholen Sie dieses Muster mit einem Zähler 4 und einer fortlaufenden ungeraden Zahl im Nenner. Je öfter Sie dies tun, desto näher kommen Sie pi.

2. Profitieren Sie von den Nilakantha-Produkten. Dies ist eine weitere unendliche Reihe, mit der Sie Pi berechnen können und die nicht schwer zu verstehen ist. Obwohl etwas komplizierter, kann man damit pi viel schneller berechnen als mit der Leibniz-Formel.
Methode 3 von 5: Berechnen von Pi mit dem Buffon-Nadelproblem

1. Versuchen Sie das folgende Experiment, um Pi zu berechnen, indem Sie Hot Dogs werfen. Pi kommt auch in dem Gedankenexperiment namens Buffon`s Needle Problem vor, das versucht, die Wahrscheinlichkeit zu bestimmen, mit der zufällig geworfene, ähnlich geformte Objekte zwischen oder auf einer Reihe paralleler Linien auf dem Boden landen. Es stellt sich heraus, dass, wenn der Abstand zwischen den Linien gleich der Länge der geworfenen Objekte ist, die Anzahl der Landungen der Objekte auf einer Linie nach vielen Würfen verwendet werden kann, um pi . zu berechnen.
- Wissenschaftler und Mathematiker haben noch keine Möglichkeit gefunden, Pi genau zu berechnen, weil sie noch kein Material gefunden haben, das so dünn ist, dass man damit exakte Berechnungen durchführen kann.
Methode 4 von 5: Berechnen von Pi mit einem Limit

1. Wähle eine große Zahl. Je größer die Zahl, desto genauer wird Ihre Berechnung sein.

2. Verwenden Sie die Zahl, die wir x nennen, in dieser Formel, um pi zu berechnen:x *Sünde (180 / x). Damit dies funktioniert, stellen Sie sicher, dass Ihr Taschenrechner auf Grad eingestellt ist. Der Grund, warum dies als Grenze bezeichnet wird, ist, dass das Ergebnis auf pi . beschränkt ist. Wenn Sie Ihre Zahl x erhöhen, nähert sich das Ergebnis dem Wert von pi . immer mehr an.
Methode 5 von 5: Arkussinus- und Umkehrsinusfunktion
1. Wählen Sie eine Zahl zwischen -1 und 1. Dies liegt daran, dass der Arkussinus für Zahlen größer als 1 oder kleiner als -1 . nicht definiert ist.
2. Verwenden Sie die Zahl in der folgenden Formel und das Ergebnis ist ungefähr gleich pi.
Tipps
- Das Berechnen von Pi macht Spaß und ist eine Herausforderung, aber wenn Sie zu viele Nachkommastellen berechnen, wird es nicht viel nützen .Astronomen sagen, dass es nicht mehr als 39 Dezimalstellen braucht, bis die Zahl Pi hochgenaue Berechnungen durchführen kann.
Оцените, пожалуйста статью