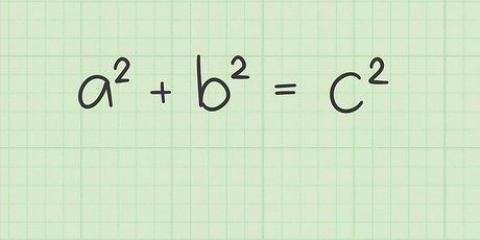Angenommen, wir wissen, dass die Hypotenuse eine Länge von 5 hat und eine der anderen Seiten eine Länge von 3 . hat. Die Länge der verbleibenden Seite ist unbekannt. Da zwei der Seiten bekannt sind, können wir die Länge der unbekannten Seite berechnen! Wir werden dieses Beispiel später noch einmal verwenden. Wenn die Länge von zwei der Seiten unbekannt sind, dann muss man die Länge von mindestens einer weiteren Seite bestimmen, um den Satz des Pythagoras anwenden zu können. Die trigonometrischen Grundfunktionen können Ihnen dabei helfen, sofern Sie einen der anderen nicht rechten Winkel des Dreiecks kennen. 
In unserem Beispiel kennen wir die Länge einer Seite und die der Hypotenuse (3 & 5), also schreiben wir unsere Gleichung so: 3² + b² = 5² 
In unserem Beispiel quadrieren wir 3 und 5, um resp . zu erhalten. 9 und 25 bekommen. Wir können nun die Gleichung umschreiben als 9 + b² = 25. 
In unserem Beispiel lautet die Gleichung nun 9 + b² = 25. zu b² wir subtrahieren 9 von beiden Seiten der Gleichung. Dies lässt uns mit b² = 16. 
In unserem Beispiel, b² = 16, lautet die Gleichung nach dem Ziehen der Quadratwurzeln b = 4. Wir können also sagen, dass die Länge der unbekannten Seite unseres Dreiecks gleich ist 4. 
Nehmen wir ein Beispiel aus der realen Welt. Eine Leiter lehnt an einer Wand. Das untere Ende der Leiter ist 5 Meter von der Wand entfernt. Die Leiter reicht bis zu 20 Meter, gemessen von der Unterseite der Wand. Wie lang ist die Leiter? "5 Meter ist der Abstand zur Wand“ und "die Leiter ist 20 Meter hoch“. Dies gibt einen Hinweis auf die Länge der Seiten des Dreiecks. Da Wand und Boden einen rechten Winkel bilden sollen und die Leiter schräg zur Wand steht, können wir diese Anordnung als rechtwinkliges Dreieck betrachten, dessen Seitenlängen a = 5 und b = 20 . haben. Die Leiterlänge ist die Hypotenuse, die unbekannte Variable c. Wenden wir den Satz des Pythagoras hier an: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² Quadrat (425) = c c = 20,6 . Die Länge der Leiter beträgt (ungefähr) 20,6 Meter. 


Angenommen, wir haben die Punkte (6.1) und (3.5). Die Länge der horizontalen Seite unseres Dreiecks beträgt: |x1 - x2| |3 - 6| | -3 | = 3 Die Länge der vertikalen Seite beträgt: |y1 - ja2| |1 - 5| | -4 | = 4 Wir können also sagen, dass die Länge der Seiten unseres rechtwinkligen Dreiecks gleich a = 3 und b = 4 . ist. 
Da wir in unserem Beispiel die Punkte (3,5) und (6.1) kennen und die Seitenlängen a=3 und b=4 sind, bestimmen wir die Hypotenuse wie folgt: sqrt(x) bedeutet "die Quadratwurzel von x". Vergiss nicht, deine Antworten immer zu überprüfen. Wenn eine Antwort nicht richtig ist, überprüfen Sie Ihre Berechnungen oder beginnen Sie von vorne. Wenn Sie nur eine Seite des Dreiecks kennen, aber auch einen der anderen Winkel (als den rechten Winkel), berechnen Sie zuerst eine andere Seite mit dem, was Sie über die Trigonometrie wissen (sin, cos, tan) oder die Proportionen 30-60-90 / 45-45-90. Noch eine Prüfung – die längste Seite steht dem größten Winkel gegenüber und die kürzeste Seite dem kleinsten Winkel.
Verwendung des satzes des pythagoras
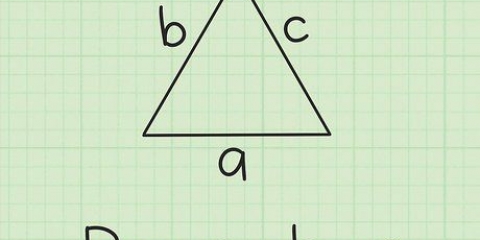
Der Satz des Pythagoras beschreibt die Länge der Seiten eines rechtwinkligen Dreiecks so elegant und praktisch, dass er noch heute weit verbreitet ist. Dies besagt, dass für jedes rechtwinklige Dreieck die Summe der Quadrate der rechten Seiten gleich dem Quadrat der Hypotenuse ist. Mit anderen Worten, für ein rechtwinkliges Dreieck (ein Dreieck mit Seiten, die senkrecht aufeinander stehen), mit Seiten der Länge a und b und einer Hypotenuse der Länge c: a + b = c. Der Satz des Pythagoras ist eine der Säulen der Geometrie und hat zahlreiche praktische Anwendungen – mit diesem Satz ist es beispielsweise sehr einfach, den Abstand zwischen zwei Punkten in einer Ebene zu bestimmen.
Schritte
Methode 1 von 2: Die Länge der Seiten eines rechtwinkligen Dreiecks

1. Prüfen Sie, ob Sie es mit einem rechtwinkligen Dreieck zu tun haben. Der Satz des Pythagoras kann nur für rechtwinklige Dreiecke verwendet werden. Bevor Sie fortfahren, ist es wichtig, dass Ihr Dreieck die Definition eines rechtwinkligen Dreiecks erfüllt. Zum Glück gibt es hier nur einen entscheidenden Faktor – eine der Ecken des Dreiecks muss einen 90-Grad-Winkel haben.
- Ein Hinweis ist, dass rechte Winkel oft mit einer kleinen eckigen Klammer gekennzeichnet sind, um anzuzeigen, dass es sich um einen 90-Grad-Winkel handelt. Sehen Sie nach, ob sich in einer der Ecken Ihres Dreiecks eine solche Klammer befindet.

2. Weisen Sie den Seiten Ihres Dreiecks die Variablen a, b und c zu. Im Satz des Pythagoras beziehen sich die Variablen a und b auf die rechten Seiten Ihres Dreiecks und die Variable c auf die Hypotenuse – die lange Seite gegenüber dem rechten Winkel. Zu Beginn weisen Sie also die Variablen a und b (die Reihenfolge spielt keine Rolle) den geraden Seiten zu und Sie weisen c der Hypotenuse zu.

3. Bestimmen Sie, welche Seite des Dreiecks Sie wissen möchten. Mit dem Satz des Pythagoras können Sie die Länge einer beliebigen Seite eines Dreiecks bestimmen, sofern zwei der Seiten bekannt sind. Bestimmen Sie, welche der Seiten eine unbekannte Länge hat--ein, B, und/oderC. Wenn nur einer unbekannt ist, können Sie weitermachen.

4. Berechnen Sie mit der Gleichung und den Bekannten. Setze die Werte für die Längen der Seiten deines Dreiecks in die Gleichung a + b = c . ein. Denken Sie daran, dass a und b die geraden Seiten sind und c die Hypotenuse.

5. Berechnen Sie die Quadrate. Um Ihre Gleichung zu lösen, beginnen Sie damit, jede der bekannten Seiten zu quadrieren. Wenn Sie dies einfacher finden, können Sie die Leistung belassen und später quadrieren.

6. Isolieren Sie die unbekannte Variable auf einer Seite des Gleichheitszeichens. Verwenden Sie optional algebraische Standardoperationen, um das Unbekannte auf eine Seite des Gleichheitszeichens und die Quadrate auf die andere Seite zu bringen. Wenn Sie versuchen, die Hypotenuse zu finden, befindet sich c bereits in der Position auf einer Seite, sodass Sie diesen Schritt überspringen können.

7. Ziehe die Quadratwurzel beider Seiten der Gleichung. Sie sollten jetzt auf der einen Seite der Gleichung ein Quadrat (Variable) und auf der anderen Seite eine Zahl haben. Ziehen Sie nun die Quadratwurzel beider Seiten ab, um die Länge der Unbekannten zu ermitteln.

8. Verwenden Sie den Satz des Pythagoras in der Praxis. Der Grund, warum der Satz des Pythagoras so häufig verwendet wird, liegt darin, dass er auf die Lösung vieler praktischer Probleme anwendbar ist. Lernen Sie, rechtwinklige Dreiecke in der Welt um Sie herum zu erkennen – überall dort, wo Sie ein rechtwinkliges Dreieck mit einem oder mehreren Objekten identifizieren können, kann der Satz des Pythagoras verwendet werden, um die Länge einer der Seiten zu bestimmen, vorausgesetzt, es gibt zwei Seiten oder Winkel sind berühmt.
Methode 2 von 2: Berechnen Sie den Abstand zwischen zwei Punkten in der Ebene

1. Definiere zwei Punkte in der Ebene. Mit dem Satz des Pythagoras lässt sich sehr einfach der Abstand zwischen zwei Punkten in der Ebene auf einer Geraden bestimmen. Alles was Sie brauchen sind die x- und y-Koordinaten von zwei beliebigen Punkten. Normalerweise werden diese Koordinaten geschrieben als (x, y).
- Um den Abstand zwischen diesen beiden Punkten zu bestimmen, betrachten wir jeden der Punkte als einen der Eckpunkte eines rechtwinkligen Dreiecks, die nicht zum rechten Winkel gehören. Dies macht es sehr einfach, die Länge von a und b zu finden, wonach c (die Hypotenuse und der Abstand zwischen den beiden Punkten) berechnet werden kann.

2. Zeichnen Sie die beiden Punkte in eine Grafik ein. In einer X-Y-Ebene ist für jeden Punkt (x, y) x ein Punkt auf der horizontalen x-Achse und y ein Punkt auf der vertikalen y-Achse. Sie können den Abstand zwischen den beiden finden, ohne sie grafisch darzustellen, aber dadurch erhalten Sie einen visuellen Hinweis, um zu überprüfen, ob Ihre Antwort sinnvoll ist.

3. Finden Sie die Länge der geraden Seiten Ihres Dreiecks. Indem Sie Ihre beiden Punkte als Winkel des Dreiecks betrachten, das an die Hypotenuse angrenzt, können Sie die Längen der Seiten a und b . ermitteln. Sie können dies tun, indem Sie das Diagramm verwenden oder die Formeln |x . verwenden1 - x2| für die horizontale Seite und |y1 - ja2| für die vertikale Seite, wobei (x1,ja1) ist der erste Punkt und (x2,ja2) der zweite Punkt.

4. Verwenden Sie den Satz des Pythagoras, um die Hypotenuse zu finden. Der Abstand zwischen den beiden Punkten ist die Länge der Hypotenuse des Dreiecks. Verwenden Sie den Satz des Pythagoras, um die Hypotenuse des Dreiecks mit den Seiten a, b und c . zu finden.
- (3)²+(4)²= c²
- c= sqrt(9+16)
- c= Quadrat(25)
- c= 5. Der Abstand zwischen (3.5) und (6.1) ist 5.
Tipps
- Wenn das Dreieck kein rechtwinkliges Dreieck ist, können Sie nicht einfach den Satz des Pythagoras verwenden.
- Die Hypotenuse ist immer:
- die Linie gegenüber dem rechten Winkel
- die längste Seite des rechtwinkligen Dreiecks
- Die Variable C im Satz des Pythagoras
"Verwendung des satzes des pythagoras"
Оцените, пожалуйста статью