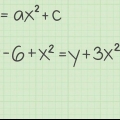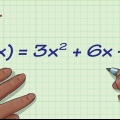Denken Sie daran, dass jede Operation auf einer Seite des Gleichheitszeichens auch auf der anderen Seite ausgeführt werden muss. Beispiel: Um mit unserem Beispiel fortzufahren, addieren wir zunächst 2 auf beiden Seiten der Gleichung. Dies gibt uns y + 2 = 5x. Dann teilen wir beide Seiten der Gleichung durch 5 und lassen (y + 2)/5 = x. Um es besser lesbar zu machen, schreiben wir die Gleichung schließlich um mit "x" Nach links: x = (y + 2)/5. 
Beispiel: Nach dem Vertauschen von x und y erhalten wir y = (x + 2)/5 
Denn x gleich 1/x ist, können Sie f(x) auch schreiben als "1/f(x)," eine andere Notation für die Umkehrung von f(x). 
Beispiel: Geben wir 4 als Wert von ein x in unserem Originalvergleich. Dies ergibt f(x) = 5(4) - 2, oder f(x) = 18. Als nächstes werden wir dieses Ergebnis in die Umkehrung. Also ersetzen wir 18 in der Umkehrfunktion als Wert von x. Dadurch erhalten wir als Ergebnis y = (18 + 2)/5 und dies ist gleich y = 4. 4 ist also der x-Wert, mit dem wir begonnen haben, und damit wissen wir, dass wir die richtige Umkehrfunktion gefunden haben.
Die umkehrung einer funktion finden
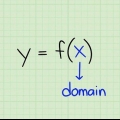
Eine Funktion in der Mathematik (normalerweise als f(x) notiert) kann man sich als eine Art Formel oder ein Programm vorstellen, in das man einen Wert eingibt "x" einsteckt, was dann einen gegebenen Wert für zurückgibt ja. Der invers einer Funktion f(x) (notiert als f(x)) ist im Wesentlichen das Gegenteil: Geben Sie a . ein ja-Wert und du bekommst das frühere x-Wert zurück. Die Umkehrung einer Funktion zu finden mag kompliziert erscheinen, aber für einfache Gleichungen benötigen Sie lediglich Kenntnisse der grundlegenden Operationen der Algebra. Lesen Sie die folgende Schritt-für-Schritt-Anleitung und sehen Sie sich das Beispiel genau an.
Schritte

1. Schreiben Sie Ihre Funktion und vertauschen Sie f(x) mit ja Falls benötigt. Deine Formel gehört ja auf der einen Seite das Gleichheitszeichen haben und auf der anderen Seite das x-Bedingungen. Wenn Sie bereits eine Gleichung in geschrieben haben ja und x Begriffe (wie zum Beispiel 2 + y = 3x), dann brauchst du nur ja durch Isolieren gelöst werden.
- Beispiel: Wir haben eine Funktion f(x) = 5x - 2 und schreiben sie um als y = 5x - 2, einfach von "f(x)" ersetzt werden durch ja.
- Hinweis: f(x) ist die Standardfunktionsnotation, aber wenn Sie mit mehreren Funktionen arbeiten, erhält jede Funktion einen anderen Anfangsbuchstaben, um sie leichter unterscheiden zu können. Zum Beispiel sind g(x) und h(x) häufig verwendete Buchstaben für Funktionen.

2. lose x an. Mit anderen Worten, nehmen Sie die erforderlichen Änderungen an x auf einer Seite des Gleichheitszeichens isolieren. Verwenden Sie dazu die Grundoperationen der Algebra: if x hat einen Koeffizienten (eine Zahl für die Variable), dividiere beide Seiten der Gleichung durch diese Zahl, um sie aufzuheben; gibt es eine Konstante innerhalb der "x"-Term, dann berechnen Sie ihn, indem Sie beide Seiten des Gleichheitszeichens addieren oder subtrahieren, und so weiter.

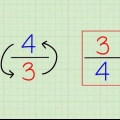
3. Vertausche die Variablen. Wechsel x von ja und umgekehrt. Die resultierende Gleichung ist die Umkehrung der ursprünglichen Funktion. Mit anderen Worten, wenn wir einen Wert für haben x Füllen Sie unsere ursprüngliche Gleichung aus, dann können wir die Antwort invers eingeben (wieder für "x") was den ursprünglichen Wert zurückgibt!

4. ersetzen ja mittels "f(x)". Umkehrfunktionen werden normalerweise als f(x) = (x Terme) notiert . Denken Sie daran, dass der Exponent -1 in diesem Fall nicht bedeutet, dass wir eine Exponentialoperation an der Funktion ausführen müssen. Es ist nur ein Hinweis darauf, dass diese Funktion die Umkehrung des Originals ist.

5. Überprüfe deine Arbeit. Versuchen Sie, eine Konstante in die ursprüngliche Funktion für einzugeben x. Wenn Sie die richtige Umkehrung gefunden haben, würden Sie den ursprünglichen Wert von finden "x" sollte es wieder sehen, wenn Sie das Ergebnis invers eingeben.
Tipps
- Sie können beide Notationen f(x) = y und f^(-1)(x) = y problemlos verwenden, wenn Sie mathematische Operationen an den Funktionen durchführen. Aber es ist besser, die Originalfunktion und die Umkehrfunktion auseinander zu halten, also versuchen Sie, sie in der gemeinsamen Notation zu halten. Bei der Umkehrfunktion ist die Notation f^(-1)(x).
- Beachten Sie, dass die Umkehrung einer Funktion normalerweise, aber nicht immer, eine Funktion selbst ist.
"Die umkehrung einer funktion finden"
Оцените, пожалуйста статью