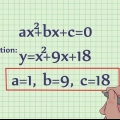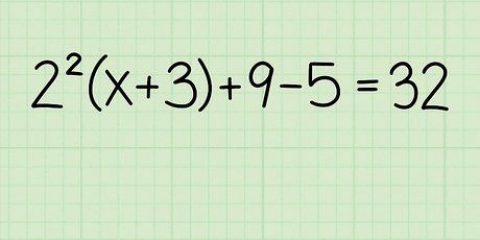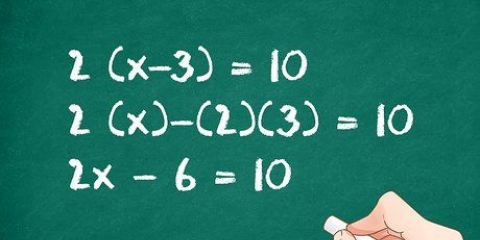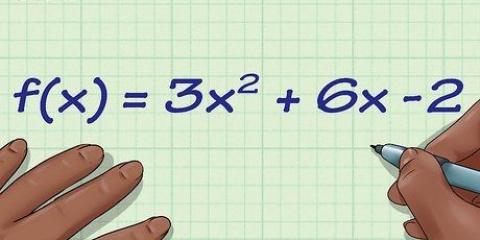Nehmen Sie den Beispielvergleich  , wobei die y-Terme nach links verschoben werden können, indem a y von beiden Seiten abgezogen wird. Die anderen Begriffe können auf die rechte Seite verschoben werden, indem auf beiden Seiten 6 hinzugefügt werden und
, wobei die y-Terme nach links verschoben werden können, indem a y von beiden Seiten abgezogen wird. Die anderen Begriffe können auf die rechte Seite verschoben werden, indem auf beiden Seiten 6 hinzugefügt werden und  von beiden Seiten abziehen. Die resultierende Gleichung ist
von beiden Seiten abziehen. Die resultierende Gleichung ist  .
. 
Sehen Sie sich den Beispielvergleich an  . Es gibt keine Beschränkung der zulässigen Werte von x für diese Gleichung. Sie müssen sich jedoch bewusst sein, dass dies die Gleichung einer Parabel mit x=0 als Mittelpunkt ist und eine Parabel keine Funktion ist, da sie kein Eins-zu-Eins-Vergleich von x- und y-Werten ist. Um diese Gleichung zu begrenzen und zu einer Funktion zu machen, für die wir eine Inverse finden können, müssen wir das Gebiet als x≥0 . definieren.
. Es gibt keine Beschränkung der zulässigen Werte von x für diese Gleichung. Sie müssen sich jedoch bewusst sein, dass dies die Gleichung einer Parabel mit x=0 als Mittelpunkt ist und eine Parabel keine Funktion ist, da sie kein Eins-zu-Eins-Vergleich von x- und y-Werten ist. Um diese Gleichung zu begrenzen und zu einer Funktion zu machen, für die wir eine Inverse finden können, müssen wir das Gebiet als x≥0 . definieren. Ebenso ist die Reichweite eingeschränkt. Beachten Sie, dass der erste Term,  , wird immer positiv oder 0 sein, für jeden Wert von x. Wenn die Gleichung dann +2 hinzufügt, ist der Bereich ein beliebiger Wert y≥2.
, wird immer positiv oder 0 sein, für jeden Wert von x. Wenn die Gleichung dann +2 hinzufügt, ist der Bereich ein beliebiger Wert y≥2. Die Definition der Domäne und des Umfangs in diesem frühen Stadium ist notwendig. Sie werden diese Definitionen später verwenden, wenn Sie den Bereich und den Geltungsbereich der Umkehrfunktion definieren. Tatsächlich wird der Bereich der Originalfunktion zum Bereich der Umkehrfunktion, und der Bereich der Originalfunktion wird zum Bereich der Umkehrfunktion. 
Arbeiten mit dem Beispielvergleich  , dieser Inversionsschritt führt zu der neuen Gleichung von
, dieser Inversionsschritt führt zu der neuen Gleichung von  .
. Ein alternatives Format besteht darin, die y-Terme durch x zu ersetzen, aber die x-Terme durch entweder zu ersetzen  oder
oder  um die Umkehrfunktion anzuzeigen.
um die Umkehrfunktion anzuzeigen. 
 (ursprüngliche Prämisse)
(ursprüngliche Prämisse) (von beiden Seiten 2 abziehen)
(von beiden Seiten 2 abziehen) (beide Seiten durch 2 teilen)
(beide Seiten durch 2 teilen)± (Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten ergibt)
(Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten ergibt) 
Siehe die Lösung der Beispielgleichung ± . Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term
. Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term  Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥2 . sein. Damit sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥0, wenn Sie die positive Lösung der Quadratwurzel nehmen, oder y≤0, wenn Sie die negative Lösung von nehmen die Quadratwurzel. Beachten Sie, dass Sie den Definitionsbereich ursprünglich als x≥0 . definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option.
Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥2 . sein. Damit sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥0, wenn Sie die positive Lösung der Quadratwurzel nehmen, oder y≤0, wenn Sie die negative Lösung von nehmen die Quadratwurzel. Beachten Sie, dass Sie den Definitionsbereich ursprünglich als x≥0 . definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option. Vergleiche den Bereich und den Bereich des Inversen mit dem Bereich und Bereich des Originals. Denken Sie daran, dass für die ursprüngliche Funktion,  , die Domäne wurde als alle Werte von x≥0 definiert und der Bereich wurde als alle Werte von y≥2 . definiert. Für die Umkehrfunktion werden nun diese Werte vertauscht, und die Domäne umfasst alle Werte von x≥2, und der Bereich umfasst alle Werte von y≥0.
, die Domäne wurde als alle Werte von x≥0 definiert und der Bereich wurde als alle Werte von y≥2 . definiert. Für die Umkehrfunktion werden nun diese Werte vertauscht, und die Domäne umfasst alle Werte von x≥2, und der Bereich umfasst alle Werte von y≥0. 
Wählen Sie als Beispiel den Wert x=1 für die ursprüngliche Gleichung  . Dies ergibt das Ergebnis y=4.
. Dies ergibt das Ergebnis y=4. Dann setzt du den Wert 4 in die Umkehrfunktion ein  . Dies ergibt tatsächlich das Ergebnis y=1. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.
. Dies ergibt tatsächlich das Ergebnis y=1. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist. 

Beachten Sie, dass diese Standardform aus einem perfekten quadratischen Term besteht,  , die dann durch die anderen beiden Elemente a und k . modifiziert wird. Um zu dieser perfekten quadratischen Form zu gelangen, müssen Sie in Ihrer quadratischen Gleichung bestimmte Bedingungen schaffen.
, die dann durch die anderen beiden Elemente a und k . modifiziert wird. Um zu dieser perfekten quadratischen Form zu gelangen, müssen Sie in Ihrer quadratischen Gleichung bestimmte Bedingungen schaffen. 
Um das Quadrat zu vervollständigen, in umgekehrter Reihenfolge arbeiten. Sie beginnen mit  und ein zweiter x-Term. Aus dem Koeffizienten dieses Termes, den Sie als `2b` definieren können, müssen Sie erhalten
und ein zweiter x-Term. Aus dem Koeffizienten dieses Termes, den Sie als `2b` definieren können, müssen Sie erhalten  sehen, um zu finden. Dies erfordert eine Kombination aus Dividieren durch zwei und dann Quadrieren dieses Ergebnisses.
sehen, um zu finden. Dies erfordert eine Kombination aus Dividieren durch zwei und dann Quadrieren dieses Ergebnisses. 
Nehmen wir zum Beispiel die quadratische Funktion  . Sie können dies vereinfachen, indem Sie alle Terme durch 2 teilen, um die resultierende Funktion zu erhalten
. Sie können dies vereinfachen, indem Sie alle Terme durch 2 teilen, um die resultierende Funktion zu erhalten  bekommen. Der Koeffizient 2 bleibt außerhalb der Klammern und wird Teil Ihrer endgültigen Lösung.
bekommen. Der Koeffizient 2 bleibt außerhalb der Klammern und wird Teil Ihrer endgültigen Lösung. Wenn alle Terme kein Vielfaches von a sind, erhalten Sie Bruchkoeffizienten. Zum Beispiel: die Funktion  wird vereinfacht zu
wird vereinfacht zu  . Rechne die Brüche sorgfältig aus.
. Rechne die Brüche sorgfältig aus. 
Wenn beispielsweise die ersten beiden Terme Ihrer quadratischen Funktion  Sie finden den notwendigen dritten Term, indem Sie 3 durch 2 (oder 3/2) teilen und dann quadrieren, um 9/4 . zu erhalten. Das quadratische
Sie finden den notwendigen dritten Term, indem Sie 3 durch 2 (oder 3/2) teilen und dann quadrieren, um 9/4 . zu erhalten. Das quadratische  ist ein perfektes Quadrat.
ist ein perfektes Quadrat. Ein weiteres Beispiel: Angenommen, die ersten beiden Terme  sind. Die Hälfte des Mittelterms ist -2, und dann quadrieren Sie es, um 4 . zu erhalten. Das resultierende perfekte Quadrat ist
sind. Die Hälfte des Mittelterms ist -2, und dann quadrieren Sie es, um 4 . zu erhalten. Das resultierende perfekte Quadrat ist  .
. 
Angenommen, Sie haben die Funktion  . Wie oben erwähnt, verwenden Sie die ersten beiden Terme, um das Quadrat zu vervollständigen. Mit dem mittleren Term von -4x generieren Sie einen dritten Term +4. Addiere 4 und subtrahiere 4 von der Gleichung in der Form
. Wie oben erwähnt, verwenden Sie die ersten beiden Terme, um das Quadrat zu vervollständigen. Mit dem mittleren Term von -4x generieren Sie einen dritten Term +4. Addiere 4 und subtrahiere 4 von der Gleichung in der Form  . Die Klammern werden nur gesetzt, um die quadratische Gleichung zu definieren, die Sie erstellen. Beachten Sie die +4 innerhalb der Klammern und die -4 außen. Vereinfache die Zahlen zum Ergebnis
. Die Klammern werden nur gesetzt, um die quadratische Gleichung zu definieren, die Sie erstellen. Beachten Sie die +4 innerhalb der Klammern und die -4 außen. Vereinfache die Zahlen zum Ergebnis  .
. 
Beachten Sie, dass für diese Funktion a=1, h=2 und k=5. Der Wert der Gleichung in dieser Form besteht darin, dass a, weil sie positiv ist, Ihnen sagt, dass die Parabel nach oben zeigt. Die Werte (h, k) geben den Scheitelpunkt am unteren Rand der Parabel an, wenn Sie ihn grafisch darstellen möchten. 
Weiter mit der Vorschaufunktion arbeiten  . Da dies im Standardformat ist, können Sie den Scheitelpunkt als x=2, y=5 . bestimmen. Um die Symmetrie zu vermeiden, arbeiten Sie also nur mit der rechten Seite des Graphen und setzen die Domäne, wenn alle Werte x≥2. Einfügen des Wertes x=2 in die Funktion ergibt y=5. Sie können sehen, dass die Werte von y mit zunehmendem x zunehmen. Daher ist der Bereich dieser Gleichung y≥5.
. Da dies im Standardformat ist, können Sie den Scheitelpunkt als x=2, y=5 . bestimmen. Um die Symmetrie zu vermeiden, arbeiten Sie also nur mit der rechten Seite des Graphen und setzen die Domäne, wenn alle Werte x≥2. Einfügen des Wertes x=2 in die Funktion ergibt y=5. Sie können sehen, dass die Werte von y mit zunehmendem x zunehmen. Daher ist der Bereich dieser Gleichung y≥5. 
Weiter mit der Funktion arbeiten  . Setzen Sie x anstelle von f(x) ein und fügen Sie y (oder f(x), wenn Sie es vorziehen) anstelle von x . ein. Dies gibt als neue Funktion
. Setzen Sie x anstelle von f(x) ein und fügen Sie y (oder f(x), wenn Sie es vorziehen) anstelle von x . ein. Dies gibt als neue Funktion  .
. 
 (ursprünglicher Ausgangspunkt)
(ursprünglicher Ausgangspunkt) (jeweils 5 von beiden Seiten abziehen)
(jeweils 5 von beiden Seiten abziehen)± (Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten liefert)
(Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten liefert) ± (addieren Sie 2 zu beiden Seiten)
(addieren Sie 2 zu beiden Seiten) 
Siehe die Lösung der Beispielgleichung ± . Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term
. Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term  Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥5 . sein. Damit als Domäne sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥2 (wenn Sie die positive Lösung der Quadratwurzel nehmen) oder y≤2 (wenn Sie die negative Lösung wählen der Quadratwurzel). Denken Sie daran, dass Sie den Definitionsbereich ursprünglich als x≥2 definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option.
Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥5 . sein. Damit als Domäne sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥2 (wenn Sie die positive Lösung der Quadratwurzel nehmen) oder y≤2 (wenn Sie die negative Lösung wählen der Quadratwurzel). Denken Sie daran, dass Sie den Definitionsbereich ursprünglich als x≥2 definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option. Vergleiche den Bereich und den Bereich des Inversen mit dem Bereich und Bereich des Originals. Denken Sie daran, dass für die ursprüngliche Funktion der Bereich als alle Werte von x≥2 und der Bereich als alle Werte von y≥5 . definiert wurde. Für diese inverse Funktion werden diese Werte vertauscht, und die Domäne umfasst jetzt alle Werte von x≥5, und der Bereich umfasst alle Werte von y≥2. 
Wählen Sie als Beispiel den Wert x=3, der in die ursprüngliche Gleichung aufgenommen werden soll  herstellen. Dies ergibt das Ergebnis y=6.
herstellen. Dies ergibt das Ergebnis y=6. Dann verarbeitest du y=6 in der Umkehrfunktion  . Dies gibt y=3 zurück, das ist die Zahl, mit der Sie begonnen haben. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.
. Dies gibt y=3 zurück, das ist die Zahl, mit der Sie begonnen haben. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist. 

Für diesen Abschnitt dieses Artikels verwenden Sie die Beispielgleichung  .
. 

Basierend auf der Arbeitsgleichung  , ergibt das das ergebnis
, ergibt das das ergebnis  .
. 
Um für die Beispielgleichung die linke Seite gleich Null zu erhalten, müssen Sie x von beiden Seiten der Gleichung subtrahieren. Das ergibt das Ergebnis  .
. 
Verlassen  . Also, x=1
. Also, x=1 Verlassen  . Also b=2
. Also b=2 Verlassen  . Also, c=(-3-x)
. Also, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Dieser letzte Schritt ist möglich, weil Sie f(x) zu einem früheren Zeitpunkt gegen die Variable x ausgetauscht haben). 




Angenommen die ursprüngliche Funktion  , wähle dein x=-2. Dies gibt y=-3 . zurück. Setzen Sie nun den Wert von x=-3 in die Umkehrfunktion ein,
, wähle dein x=-2. Dies gibt y=-3 . zurück. Setzen Sie nun den Wert von x=-3 in die Umkehrfunktion ein,  . Dies gibt -2 zurück, was tatsächlich der Wert ist, mit dem Sie begonnen haben. Deine Definition der Umkehrfunktion ist also richtig.
. Dies gibt -2 zurück, was tatsächlich der Wert ist, mit dem Sie begonnen haben. Deine Definition der Umkehrfunktion ist also richtig.
Die umkehrung einer quadratischen gleichung finden
Umkehrfunktionen können bei der Lösung vieler mathematischer Probleme sehr hilfreich sein. In der Lage zu sein, eine Funktion zu nehmen und ihre Umkehrfunktion zu finden, ist ein mächtiges Werkzeug. Bei quadratischen Gleichungen kann dies jedoch ein ziemlich komplizierter Vorgang sein. Zuerst müssen Sie die Gleichung sorgfältig definieren, indem Sie einen geeigneten Bereich und einen geeigneten Bereich bestimmen. Sie haben dann die Wahl zwischen drei Methoden zur Berechnung der Umkehrfunktion. Die Wahl der Methode ist hauptsächlich eine Frage der persönlichen Vorlieben.
Schritte
Methode 1 von 3: Die Umkehrung einer einfachen Funktion finden

1. Finden Sie eine Funktion in der Form ja = ein x 2 + C  . Wenn Sie für den Anfang die `richtige` Art von Funktion haben, können Sie die Umkehrung mit einfacher Algebra finden. Diese Form ist eine Art Variation von
. Wenn Sie für den Anfang die `richtige` Art von Funktion haben, können Sie die Umkehrung mit einfacher Algebra finden. Diese Form ist eine Art Variation von  . Wenn Sie dies mit einer quadratischen Standardfunktion vergleichen,
. Wenn Sie dies mit einer quadratischen Standardfunktion vergleichen,  , Sehen Sie, dass die mittlere Frist
, Sehen Sie, dass die mittlere Frist  wird vermisst. Eine andere Art dies zu sagen ist, dass der Wert von b null ist. Wenn Ihre Funktion diese Form hat, ist es ganz einfach, die Umkehrung zu finden.
wird vermisst. Eine andere Art dies zu sagen ist, dass der Wert von b null ist. Wenn Ihre Funktion diese Form hat, ist es ganz einfach, die Umkehrung zu finden.
 . Wenn Sie für den Anfang die `richtige` Art von Funktion haben, können Sie die Umkehrung mit einfacher Algebra finden. Diese Form ist eine Art Variation von
. Wenn Sie für den Anfang die `richtige` Art von Funktion haben, können Sie die Umkehrung mit einfacher Algebra finden. Diese Form ist eine Art Variation von  . Wenn Sie dies mit einer quadratischen Standardfunktion vergleichen,
. Wenn Sie dies mit einer quadratischen Standardfunktion vergleichen,  , Sehen Sie, dass die mittlere Frist
, Sehen Sie, dass die mittlere Frist  wird vermisst. Eine andere Art dies zu sagen ist, dass der Wert von b null ist. Wenn Ihre Funktion diese Form hat, ist es ganz einfach, die Umkehrung zu finden.
wird vermisst. Eine andere Art dies zu sagen ist, dass der Wert von b null ist. Wenn Ihre Funktion diese Form hat, ist es ganz einfach, die Umkehrung zu finden. - Deine Ausgangsfunktion muss nicht genau so aussehen
. Solange Sie es sich ansehen und sehen können, dass die Funktion nur aus besteht
Begriffe und konstante Zahlen, können Sie diese Methode verwenden.
- Angenommen, Sie beginnen mit der Gleichung
. Eine kurze Untersuchung dieser Gleichung zeigt, dass es keine Terme von gibt
zur ersten Macht sein. Diese Gleichung ist ein Kandidat für diese Methode, um eine Umkehrfunktion zu finden.

2. Vereinfachen Sie, indem Sie ähnliche Begriffe kombinieren. Die Anfangsgleichung kann mehrere Terme in einer Kombination aus Addition und Subtraktion haben. Ihr erster Schritt besteht darin, ähnliche Terme zu kombinieren, um die Gleichung zu vereinfachen, und sie in das Standardformat umzuschreiben  .
.
 .
. , wobei die y-Terme nach links verschoben werden können, indem a y von beiden Seiten abgezogen wird. Die anderen Begriffe können auf die rechte Seite verschoben werden, indem auf beiden Seiten 6 hinzugefügt werden und
, wobei die y-Terme nach links verschoben werden können, indem a y von beiden Seiten abgezogen wird. Die anderen Begriffe können auf die rechte Seite verschoben werden, indem auf beiden Seiten 6 hinzugefügt werden und  von beiden Seiten abziehen. Die resultierende Gleichung ist
von beiden Seiten abziehen. Die resultierende Gleichung ist  .
.
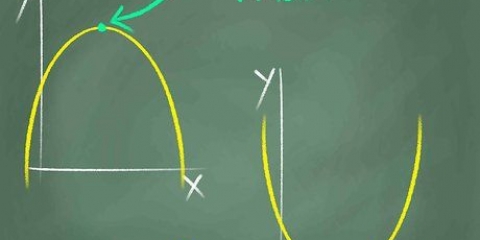
3. Bestimmen Sie den Bereich und den Bereich der vereinfachten Funktion. Denken Sie daran, dass der Bereich einer Funktion aus den möglichen Werten von x besteht, die angewendet werden können, um eine reelle Lösung zu ergeben. Der Bereich einer Funktion besteht aus den Werten von y, die zurückgegeben werden. Um den Bereich der Funktion zu bestimmen, suchen Sie nach Werten, die ein mathematisch unmögliches Ergebnis liefern. Sie geben dann die Domäne an, wenn alle anderen Werte von x. Um den Bereich zu finden, betrachten Sie die Werte von y an beliebigen Randpunkten und betrachten Sie das Verhalten der Funktion.
 . Es gibt keine Beschränkung der zulässigen Werte von x für diese Gleichung. Sie müssen sich jedoch bewusst sein, dass dies die Gleichung einer Parabel mit x=0 als Mittelpunkt ist und eine Parabel keine Funktion ist, da sie kein Eins-zu-Eins-Vergleich von x- und y-Werten ist. Um diese Gleichung zu begrenzen und zu einer Funktion zu machen, für die wir eine Inverse finden können, müssen wir das Gebiet als x≥0 . definieren.
. Es gibt keine Beschränkung der zulässigen Werte von x für diese Gleichung. Sie müssen sich jedoch bewusst sein, dass dies die Gleichung einer Parabel mit x=0 als Mittelpunkt ist und eine Parabel keine Funktion ist, da sie kein Eins-zu-Eins-Vergleich von x- und y-Werten ist. Um diese Gleichung zu begrenzen und zu einer Funktion zu machen, für die wir eine Inverse finden können, müssen wir das Gebiet als x≥0 . definieren. , wird immer positiv oder 0 sein, für jeden Wert von x. Wenn die Gleichung dann +2 hinzufügt, ist der Bereich ein beliebiger Wert y≥2.
, wird immer positiv oder 0 sein, für jeden Wert von x. Wenn die Gleichung dann +2 hinzufügt, ist der Bereich ein beliebiger Wert y≥2.
4. Vertausche die Rollen der x- und y-Terme. Ohne die Gleichung auf andere Weise zu ändern, müssen Sie alle Formen von y durch x und alle Formen von x durch y . ersetzen. Dies ist der Schritt, der die Gleichung tatsächlich `umkehrt`.
 , dieser Inversionsschritt führt zu der neuen Gleichung von
, dieser Inversionsschritt führt zu der neuen Gleichung von  .
. oder
oder  um die Umkehrfunktion anzuzeigen.
um die Umkehrfunktion anzuzeigen.
5. Schreiben Sie die inverse Gleichung in Bezug auf y . um. Wenn Sie eine Kombination algebraischer Schritte verwenden und sicherstellen, dass auf beiden Seiten der Gleichung dieselbe Operation ausgeführt wird, müssen Sie die Variable y . isolieren. Zum Vergleich  , diese Überarbeitung sieht so aus:
, diese Überarbeitung sieht so aus:
 , diese Überarbeitung sieht so aus:
, diese Überarbeitung sieht so aus: (ursprüngliche Prämisse)
(ursprüngliche Prämisse) (von beiden Seiten 2 abziehen)
(von beiden Seiten 2 abziehen) (beide Seiten durch 2 teilen)
(beide Seiten durch 2 teilen) (Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten ergibt)
(Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten ergibt)
6. Bestimmen Sie den Bereich und den Bereich der Umkehrfunktion. Untersuchen Sie wie am Anfang die invertierte Gleichung, um den Bereich und die Reichweite zu bestimmen. Wählen Sie mit zwei möglichen Lösungen die Lösung, deren Bereich und Bereich die Umkehrung des ursprünglichen Bereichs und Bereichs sind.
 . Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term
. Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term  Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥2 . sein. Damit sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥0, wenn Sie die positive Lösung der Quadratwurzel nehmen, oder y≤0, wenn Sie die negative Lösung von nehmen die Quadratwurzel. Beachten Sie, dass Sie den Definitionsbereich ursprünglich als x≥0 . definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option.
Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥2 . sein. Damit sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥0, wenn Sie die positive Lösung der Quadratwurzel nehmen, oder y≤0, wenn Sie die negative Lösung von nehmen die Quadratwurzel. Beachten Sie, dass Sie den Definitionsbereich ursprünglich als x≥0 . definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option. , die Domäne wurde als alle Werte von x≥0 definiert und der Bereich wurde als alle Werte von y≥2 . definiert. Für die Umkehrfunktion werden nun diese Werte vertauscht, und die Domäne umfasst alle Werte von x≥2, und der Bereich umfasst alle Werte von y≥0.
, die Domäne wurde als alle Werte von x≥0 definiert und der Bereich wurde als alle Werte von y≥2 . definiert. Für die Umkehrfunktion werden nun diese Werte vertauscht, und die Domäne umfasst alle Werte von x≥2, und der Bereich umfasst alle Werte von y≥0.
7. Überprüfen Sie, ob Ihre Umkehrfunktion funktioniert. Um sicherzustellen, dass Ihre Arbeit korrekt ist und Ihre Umkehrung die richtige Gleichung ist, wählen Sie einen beliebigen Wert für x und setzen Sie ihn in die ursprüngliche Gleichung, um y . zu finden. Setzen Sie dann diesen Wert von y an die Stelle von x in Ihre inverse Gleichung und sehen Sie, ob Sie die Zahl erhalten, mit der Sie begonnen haben. Wenn ja, ist Ihre Umkehrfunktion korrekt.
 . Dies ergibt das Ergebnis y=4.
. Dies ergibt das Ergebnis y=4. . Dies ergibt tatsächlich das Ergebnis y=1. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.
. Dies ergibt tatsächlich das Ergebnis y=1. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.Methode 2 von 3: Das Quadrat vervollständigen, um die Umkehrfunktion zu finden

1. Gib der quadratischen Gleichung die richtige Form. Um die Umkehrung zu finden, musst du mit der Gleichung der Form beginnen  . Gegebenenfalls müssen Sie ähnliche Terme kombinieren, um die Gleichung in diesem Format zu erhalten. Mit der so geschriebenen Gleichung kannst du etwas mehr darüber erzählen.
. Gegebenenfalls müssen Sie ähnliche Terme kombinieren, um die Gleichung in diesem Format zu erhalten. Mit der so geschriebenen Gleichung kannst du etwas mehr darüber erzählen.
 . Gegebenenfalls müssen Sie ähnliche Terme kombinieren, um die Gleichung in diesem Format zu erhalten. Mit der so geschriebenen Gleichung kannst du etwas mehr darüber erzählen.
. Gegebenenfalls müssen Sie ähnliche Terme kombinieren, um die Gleichung in diesem Format zu erhalten. Mit der so geschriebenen Gleichung kannst du etwas mehr darüber erzählen. - Das erste, was Sie bemerken werden, ist der Wert des Koeffizienten a. wenn ein>0, dann definiert die Gleichung eine Parabel, deren Enden nach oben zeigen (Talparabel). wenn ein<0, dann definiert die Gleichung eine Parabel, deren Enden nach unten zeigen (Bergparabel). Beachten Sie, dass a≠0. Wenn nicht, wäre dies eine lineare Funktion und keine quadratische.

2. Erkennen Sie das Standardformat des quadratischen. Bevor Sie die Umkehrfunktion finden können, müssen Sie die Gleichung in das Standardformat umschreiben. Das Standardformat für eine quadratische Funktion ist  . Die numerischen Terme a, h und k werden ausgewertet, wenn Sie die Gleichung umwandeln, indem Sie das Quadrat berechnen.
. Die numerischen Terme a, h und k werden ausgewertet, wenn Sie die Gleichung umwandeln, indem Sie das Quadrat berechnen.
 . Die numerischen Terme a, h und k werden ausgewertet, wenn Sie die Gleichung umwandeln, indem Sie das Quadrat berechnen.
. Die numerischen Terme a, h und k werden ausgewertet, wenn Sie die Gleichung umwandeln, indem Sie das Quadrat berechnen. , die dann durch die anderen beiden Elemente a und k . modifiziert wird. Um zu dieser perfekten quadratischen Form zu gelangen, müssen Sie in Ihrer quadratischen Gleichung bestimmte Bedingungen schaffen.
, die dann durch die anderen beiden Elemente a und k . modifiziert wird. Um zu dieser perfekten quadratischen Form zu gelangen, müssen Sie in Ihrer quadratischen Gleichung bestimmte Bedingungen schaffen.
3. Denken Sie an die Form einer perfekten quadratischen Funktion zurück. Denken Sie daran, dass eine quadratische Funktion, die ein perfektes Quadrat ist, aus zwei Binomialen von entsteht  , oder
, oder  . Wenn Sie diese Multiplikation durchführen, erhalten Sie
. Wenn Sie diese Multiplikation durchführen, erhalten Sie  . Der erste Term des Quadrats ist also der erste Term des Binomials, quadriert, und der letzte Term des Quadrats ist das Quadrat des zweiten Terms des Binomials. Der mittlere Term besteht aus dem doppelten Produkt der beiden Terme, in diesem Fall
. Der erste Term des Quadrats ist also der erste Term des Binomials, quadriert, und der letzte Term des Quadrats ist das Quadrat des zweiten Terms des Binomials. Der mittlere Term besteht aus dem doppelten Produkt der beiden Terme, in diesem Fall  .
.
 , oder
, oder  . Wenn Sie diese Multiplikation durchführen, erhalten Sie
. Wenn Sie diese Multiplikation durchführen, erhalten Sie  . Der erste Term des Quadrats ist also der erste Term des Binomials, quadriert, und der letzte Term des Quadrats ist das Quadrat des zweiten Terms des Binomials. Der mittlere Term besteht aus dem doppelten Produkt der beiden Terme, in diesem Fall
. Der erste Term des Quadrats ist also der erste Term des Binomials, quadriert, und der letzte Term des Quadrats ist das Quadrat des zweiten Terms des Binomials. Der mittlere Term besteht aus dem doppelten Produkt der beiden Terme, in diesem Fall  .
. und ein zweiter x-Term. Aus dem Koeffizienten dieses Termes, den Sie als `2b` definieren können, müssen Sie erhalten
und ein zweiter x-Term. Aus dem Koeffizienten dieses Termes, den Sie als `2b` definieren können, müssen Sie erhalten  sehen, um zu finden. Dies erfordert eine Kombination aus Dividieren durch zwei und dann Quadrieren dieses Ergebnisses.
sehen, um zu finden. Dies erfordert eine Kombination aus Dividieren durch zwei und dann Quadrieren dieses Ergebnisses.
4. Stellen Sie sicher, dass der Koeffizient von x 2  1 ist. Erinnerst du dich an die ursprüngliche Form der quadratischen Funktion
1 ist. Erinnerst du dich an die ursprüngliche Form der quadratischen Funktion  . Wenn der erste Koeffizient etwas anderes als 1 ist, müssen Sie alle Terme durch diesen Wert dividieren, um a=1 . zu erhalten.
. Wenn der erste Koeffizient etwas anderes als 1 ist, müssen Sie alle Terme durch diesen Wert dividieren, um a=1 . zu erhalten.
 1 ist. Erinnerst du dich an die ursprüngliche Form der quadratischen Funktion
1 ist. Erinnerst du dich an die ursprüngliche Form der quadratischen Funktion  . Wenn der erste Koeffizient etwas anderes als 1 ist, müssen Sie alle Terme durch diesen Wert dividieren, um a=1 . zu erhalten.
. Wenn der erste Koeffizient etwas anderes als 1 ist, müssen Sie alle Terme durch diesen Wert dividieren, um a=1 . zu erhalten. . Sie können dies vereinfachen, indem Sie alle Terme durch 2 teilen, um die resultierende Funktion zu erhalten
. Sie können dies vereinfachen, indem Sie alle Terme durch 2 teilen, um die resultierende Funktion zu erhalten  bekommen. Der Koeffizient 2 bleibt außerhalb der Klammern und wird Teil Ihrer endgültigen Lösung.
bekommen. Der Koeffizient 2 bleibt außerhalb der Klammern und wird Teil Ihrer endgültigen Lösung. wird vereinfacht zu
wird vereinfacht zu  . Rechne die Brüche sorgfältig aus.
. Rechne die Brüche sorgfältig aus.
5. Finden Sie die Hälfte des mittleren Koeffizienten und quadrieren Sie ihn. Sie haben bereits die ersten beiden Terme der quadratischen Formel. Das sind die Begriffe  und der Koeffizient, der den x-Term repräsentiert. Nimmst du diesen Koeffizienten als seinen Wert, kannst du die Zahl addieren oder subtrahieren, die benötigt wird, um ein perfektes Quadrat zu bilden. Erinnern Sie sich von oben, dass der erforderliche dritte Term des Quadrats dieser zweite Koeffizient ist, geteilt durch zwei, und dann quadriert.
und der Koeffizient, der den x-Term repräsentiert. Nimmst du diesen Koeffizienten als seinen Wert, kannst du die Zahl addieren oder subtrahieren, die benötigt wird, um ein perfektes Quadrat zu bilden. Erinnern Sie sich von oben, dass der erforderliche dritte Term des Quadrats dieser zweite Koeffizient ist, geteilt durch zwei, und dann quadriert.
 und der Koeffizient, der den x-Term repräsentiert. Nimmst du diesen Koeffizienten als seinen Wert, kannst du die Zahl addieren oder subtrahieren, die benötigt wird, um ein perfektes Quadrat zu bilden. Erinnern Sie sich von oben, dass der erforderliche dritte Term des Quadrats dieser zweite Koeffizient ist, geteilt durch zwei, und dann quadriert.
und der Koeffizient, der den x-Term repräsentiert. Nimmst du diesen Koeffizienten als seinen Wert, kannst du die Zahl addieren oder subtrahieren, die benötigt wird, um ein perfektes Quadrat zu bilden. Erinnern Sie sich von oben, dass der erforderliche dritte Term des Quadrats dieser zweite Koeffizient ist, geteilt durch zwei, und dann quadriert. Sie finden den notwendigen dritten Term, indem Sie 3 durch 2 (oder 3/2) teilen und dann quadrieren, um 9/4 . zu erhalten. Das quadratische
Sie finden den notwendigen dritten Term, indem Sie 3 durch 2 (oder 3/2) teilen und dann quadrieren, um 9/4 . zu erhalten. Das quadratische  ist ein perfektes Quadrat.
ist ein perfektes Quadrat. sind. Die Hälfte des Mittelterms ist -2, und dann quadrieren Sie es, um 4 . zu erhalten. Das resultierende perfekte Quadrat ist
sind. Die Hälfte des Mittelterms ist -2, und dann quadrieren Sie es, um 4 . zu erhalten. Das resultierende perfekte Quadrat ist  .
.
6. Addiere und subtrahiere gleichzeitig den erforderlichen dritten Term. Das ist ein kniffliges Konzept, aber es funktioniert. Das Addieren und Subtrahieren derselben Zahl an verschiedenen Stellen Ihrer Funktion ändert den Wert der Funktion nicht wirklich. Auf diese Weise erhalten Sie jedoch Ihre Funktion in der richtigen Form.
 . Wie oben erwähnt, verwenden Sie die ersten beiden Terme, um das Quadrat zu vervollständigen. Mit dem mittleren Term von -4x generieren Sie einen dritten Term +4. Addiere 4 und subtrahiere 4 von der Gleichung in der Form
. Wie oben erwähnt, verwenden Sie die ersten beiden Terme, um das Quadrat zu vervollständigen. Mit dem mittleren Term von -4x generieren Sie einen dritten Term +4. Addiere 4 und subtrahiere 4 von der Gleichung in der Form  . Die Klammern werden nur gesetzt, um die quadratische Gleichung zu definieren, die Sie erstellen. Beachten Sie die +4 innerhalb der Klammern und die -4 außen. Vereinfache die Zahlen zum Ergebnis
. Die Klammern werden nur gesetzt, um die quadratische Gleichung zu definieren, die Sie erstellen. Beachten Sie die +4 innerhalb der Klammern und die -4 außen. Vereinfache die Zahlen zum Ergebnis  .
.
7. Faktorisieren Sie die quadratische Gleichung. Das Polynom in Klammern ist eine quadratische Gleichung, die Sie umschreiben können als  . Im Beispiel aus dem vorherigen Schritt (
. Im Beispiel aus dem vorherigen Schritt ( ) faktorisieren Sie den quadratischen Faktor in
) faktorisieren Sie den quadratischen Faktor in  . Kopiere den Rest der Gleichung, sodass deine Lösung
. Kopiere den Rest der Gleichung, sodass deine Lösung  wird. Dies ist die gleiche Funktion wie Ihre ursprüngliche quadratische Gleichung (
wird. Dies ist die gleiche Funktion wie Ihre ursprüngliche quadratische Gleichung ( ), umgeschrieben als Standardform
), umgeschrieben als Standardform  .
.
 . Im Beispiel aus dem vorherigen Schritt (
. Im Beispiel aus dem vorherigen Schritt ( ) faktorisieren Sie den quadratischen Faktor in
) faktorisieren Sie den quadratischen Faktor in  . Kopiere den Rest der Gleichung, sodass deine Lösung
. Kopiere den Rest der Gleichung, sodass deine Lösung  wird. Dies ist die gleiche Funktion wie Ihre ursprüngliche quadratische Gleichung (
wird. Dies ist die gleiche Funktion wie Ihre ursprüngliche quadratische Gleichung ( ), umgeschrieben als Standardform
), umgeschrieben als Standardform  .
.
8. Definieren Sie die Domäne und den Umfang der Funktion. Die Domäne ist die Menge von x-Werten, die als Eingaben für die Funktion verwendet werden können. Der Bereich ist die Menge der y-Werte, die das Ergebnis sein können. Denken Sie daran, dass eine Parabel keine Funktion mit einer definierbaren Inversen ist, da es aufgrund der Symmetrie der Parabel keine Eins-zu-Eins-Beziehung zwischen x-Werten und y-Werten gibt. Um dieses Problem zu lösen, müssen Sie den Definitionsbereich als alle Werte von x definieren, die größer sind als x=h, der Scheitelpunkt der Parabel.
 . Da dies im Standardformat ist, können Sie den Scheitelpunkt als x=2, y=5 . bestimmen. Um die Symmetrie zu vermeiden, arbeiten Sie also nur mit der rechten Seite des Graphen und setzen die Domäne, wenn alle Werte x≥2. Einfügen des Wertes x=2 in die Funktion ergibt y=5. Sie können sehen, dass die Werte von y mit zunehmendem x zunehmen. Daher ist der Bereich dieser Gleichung y≥5.
. Da dies im Standardformat ist, können Sie den Scheitelpunkt als x=2, y=5 . bestimmen. Um die Symmetrie zu vermeiden, arbeiten Sie also nur mit der rechten Seite des Graphen und setzen die Domäne, wenn alle Werte x≥2. Einfügen des Wertes x=2 in die Funktion ergibt y=5. Sie können sehen, dass die Werte von y mit zunehmendem x zunehmen. Daher ist der Bereich dieser Gleichung y≥5.
9. Vertausche die x- und y-Werte. Dies ist der Schritt, in dem Sie beginnen, indem Sie die Umkehrform der Gleichung finden. Lassen Sie die Gleichung vollständig, außer dass Sie diese Variablen vertauschen.
 . Setzen Sie x anstelle von f(x) ein und fügen Sie y (oder f(x), wenn Sie es vorziehen) anstelle von x . ein. Dies gibt als neue Funktion
. Setzen Sie x anstelle von f(x) ein und fügen Sie y (oder f(x), wenn Sie es vorziehen) anstelle von x . ein. Dies gibt als neue Funktion  .
.
10. Schreiben Sie die inverse Gleichung in Bezug auf y . um. Isolieren Sie die Variable y . mit einer Kombination algebraischer Schritte und stellen Sie sicher, dass Sie dieselbe Operation gleichmäßig auf beiden Seiten der Gleichung ausführen. Für den Arbeitsvergleich  diese Überarbeitung sieht so aus:
diese Überarbeitung sieht so aus:
 diese Überarbeitung sieht so aus:
diese Überarbeitung sieht so aus: (ursprünglicher Ausgangspunkt)
(ursprünglicher Ausgangspunkt) (jeweils 5 von beiden Seiten abziehen)
(jeweils 5 von beiden Seiten abziehen) (Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten liefert)
(Quadratwurzel beider Seiten; denken Sie daran, dass die Quadratwurzel sowohl positive als auch negative mögliche Antworten liefert) (addieren Sie 2 zu beiden Seiten)
(addieren Sie 2 zu beiden Seiten)
11. Bestimmen Sie den Bereich und den Bereich der Umkehrfunktion. Untersuchen Sie wie am Anfang die inverse Gleichung, um den Bereich und die Reichweite zu bestimmen. Wählen Sie mit zwei möglichen Lösungen die Lösung, deren Bereich und Bereich die Umkehrung des ursprünglichen Bereichs und Bereichs sind.
 . Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term
. Da die Quadratwurzelfunktion für negative Werte nicht definiert ist, muss der Term  Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥5 . sein. Damit als Domäne sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥2 (wenn Sie die positive Lösung der Quadratwurzel nehmen) oder y≤2 (wenn Sie die negative Lösung wählen der Quadratwurzel). Denken Sie daran, dass Sie den Definitionsbereich ursprünglich als x≥2 definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option.
Sei immer positiv. Daher müssen die zulässigen Werte von x (der Domäne) x≥5 . sein. Damit als Domäne sind die resultierenden Werte von y (der Bereich) entweder alle Werte y≥2 (wenn Sie die positive Lösung der Quadratwurzel nehmen) oder y≤2 (wenn Sie die negative Lösung wählen der Quadratwurzel). Denken Sie daran, dass Sie den Definitionsbereich ursprünglich als x≥2 definiert haben, um die Umkehrfunktion zu finden. Daher ist die richtige Lösung für die Umkehrfunktion die positive Option.
12. Überprüfen Sie, ob Ihre Umkehrfunktion funktioniert. Um sicherzustellen, dass Ihre Arbeit korrekt ist und Ihre Umkehrung die richtige Gleichung ist, wählen Sie einen beliebigen Wert für x und setzen Sie ihn in die ursprüngliche Gleichung, um y . zu finden. Setzen Sie dann diesen Wert von y an die Stelle von x in Ihre inverse Gleichung und sehen Sie, ob Sie die Zahl erhalten, mit der Sie begonnen haben. Wenn ja, dann ist deine Umkehrfunktion korrekt.
 herstellen. Dies ergibt das Ergebnis y=6.
herstellen. Dies ergibt das Ergebnis y=6. . Dies gibt y=3 zurück, das ist die Zahl, mit der Sie begonnen haben. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.
. Dies gibt y=3 zurück, das ist die Zahl, mit der Sie begonnen haben. Sie können daraus schließen, dass Ihre Umkehrfunktion korrekt ist.Methode 3 von 3: Verwenden der Quadratformel

1. Verwenden Sie die quadratische Formel zum Lösen von x. Denken Sie daran, dass es beim Lösen quadratischer Gleichungen eine Methode gibt, sie zu faktorisieren (wenn möglich). Wenn die Faktorisierung nicht funktioniert, können Sie die Quadratformel verwenden, die die reellen Lösungen für jede quadratische Gleichung ergibt. Sie können auch die Quadratformel als Methode verwenden, um Umkehrfunktionen zu finden.
- Die Quadratformel lautet x=[-b±√(b^2-4ac)]/2a.
- Beachten Sie, dass die Quadratformel zwei mögliche Lösungen liefert, eine positive und eine negative. Sie treffen diese Wahl basierend auf der Bestimmung der Domäne und des Umfangs der Funktion.

2. Beginnen Sie mit einer quadratischen Gleichung, um die Umkehrung zu finden. Ihre quadratische Gleichung sollte im Format . beginnen  . Führen Sie die algebraischen Schritte aus, die erforderlich sind, um Ihre Gleichung in diese Form zu bringen.
. Führen Sie die algebraischen Schritte aus, die erforderlich sind, um Ihre Gleichung in diese Form zu bringen.
 . Führen Sie die algebraischen Schritte aus, die erforderlich sind, um Ihre Gleichung in diese Form zu bringen.
. Führen Sie die algebraischen Schritte aus, die erforderlich sind, um Ihre Gleichung in diese Form zu bringen. .
.
3. Zeichnen Sie die Gleichung, um die Domäne und den Bereich zu bestimmen. Stellen Sie die Funktion grafisch dar, entweder mit einem Grafikrechner oder zeichnen Sie mehrere Punkte, bis Sie die Parabel zeichnen können. Sie werden sehen, dass diese Gleichung eine Parabel mit dem höchsten Punkt bei (-1,-4) definiert. Um dies als eine Funktion zu definieren, die eine Umkehrung hat, definieren Sie den Bereich als alle Werte von x≤-1. Der Bereich ist dann alle Werte y≥-4.

4. Vertausche die Variablen x und y. Um das Inverse zu finden, vertausche die Variablen x und y. Lassen Sie die Gleichung unverändert, außer vertauschen Sie die Variablen. Ersetze in diesem Stadium x durch f(x).
 , ergibt das das ergebnis
, ergibt das das ergebnis  .
.
5. Setze die linke Seite der Gleichung gleich null. Denken Sie daran, dass Sie zur Verwendung der quadratischen Formel die Gleichung gleich Null setzen müssen, und verwenden Sie dann die Koeffizienten in der Formel. In ähnlicher Weise beginnt diese Methode zum Auffinden einer inversen Funktion, indem die Gleichung gleich Null gesetzt wird.
 .
.
6. Definieren Sie die Variablen neu, damit sie der Quadratformel entsprechen. Dieser Schritt ist ein bisschen knifflig. Wisse, dass sich die Quadratformel nach x auflöst, in der Gleichung  . Also, für die Gleichung, die du jetzt hast,
. Also, für die Gleichung, die du jetzt hast,  , Um dieser Klassifizierung zu entsprechen, müssen Sie die Begriffe wie folgt neu definieren:
, Um dieser Klassifizierung zu entsprechen, müssen Sie die Begriffe wie folgt neu definieren:
 . Also, für die Gleichung, die du jetzt hast,
. Also, für die Gleichung, die du jetzt hast,  , Um dieser Klassifizierung zu entsprechen, müssen Sie die Begriffe wie folgt neu definieren:
, Um dieser Klassifizierung zu entsprechen, müssen Sie die Begriffe wie folgt neu definieren: . Also, x=1
. Also, x=1 . Also b=2
. Also b=2 . Also, c=(-3-x)
. Also, c=(-3-x)
7. Lösen Sie die Quadratformel mit diesen neu definierten Werten. Normalerweise würden Sie die Werte von a, b und c in der Quadratformel verarbeiten, um nach x . aufzulösen. Denken Sie jedoch daran, dass Sie zuvor x und y vertauscht haben, um die Umkehrfunktion zu finden. Wenn Sie also die Quadratformel verwenden, um nach x aufzulösen, lösen Sie tatsächlich y oder die f-Umkehrung auf. Die Schritte zum Lösen der Quadratformel funktionieren wie folgt:

8. Schreiben Sie die beiden möglichen Lösungen auf. Beachten Sie, dass die Quadratformel mit dem ±-Symbol zwei mögliche Ergebnisse liefert. Schreiben Sie die beiden getrennten Lösungen auf, um die Bestimmung der Domäne und des Bereichs zu erleichtern, und geben Sie die richtige endgültige Lösung an. Diese beiden Lösungen sind:



9. Bestimmen Sie den Bereich und den Bereich der Umkehrfunktion. Beachten Sie, dass zum Definieren der Quadratwurzel die Domäne x≥-4 . sein muss. Denken Sie daran, dass der Bereich der ursprünglichen Funktion x≤-1 war und der Bereich y≥-4 . war. Um die entsprechende Umkehrfunktion zu wählen, benötigen Sie die zweite Lösung,  wähle als die richtige Umkehrfunktion.
wähle als die richtige Umkehrfunktion.
 wähle als die richtige Umkehrfunktion.
wähle als die richtige Umkehrfunktion.
10. Überprüfen Sie, ob Ihre Umkehrfunktion korrekt ist. Um sicherzustellen, dass Ihre Arbeit korrekt ist und Ihre Umkehrung die richtige Gleichung ist, wählen Sie einen beliebigen Wert für x und setzen Sie ihn in die ursprüngliche Gleichung ein, um y . zu finden. Setzen Sie dann diesen Wert von y an die Stelle von x in Ihre inverse Gleichung und sehen Sie, ob Sie die Zahl erhalten, mit der Sie begonnen haben. Wenn ja, dann ist deine Umkehrfunktion korrekt.
 , wähle dein x=-2. Dies gibt y=-3 . zurück. Setzen Sie nun den Wert von x=-3 in die Umkehrfunktion ein,
, wähle dein x=-2. Dies gibt y=-3 . zurück. Setzen Sie nun den Wert von x=-3 in die Umkehrfunktion ein,  . Dies gibt -2 zurück, was tatsächlich der Wert ist, mit dem Sie begonnen haben. Deine Definition der Umkehrfunktion ist also richtig.
. Dies gibt -2 zurück, was tatsächlich der Wert ist, mit dem Sie begonnen haben. Deine Definition der Umkehrfunktion ist also richtig. "Die umkehrung einer quadratischen gleichung finden"
Оцените, пожалуйста статью