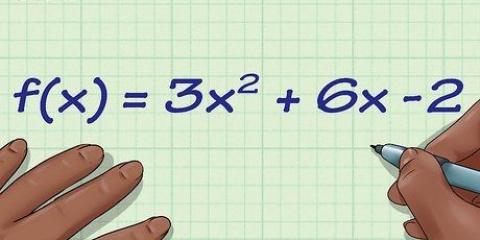Zum Beispiel: die Standardfunktion f(x) = 2x +16x + 39. Hier haben wir a = 2, b = 16 und c = 39. In Vertex-Notation: f(x) = 4(x - 5) + 12. Hier haben wir a = 4, h = 5 und k = 12. 
Beispiel 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). Wenn wir dies lösen, sehen wir, dass h = -4. Beispiel 2. (f(x) = 4(x - 5) + 12), sehen wir sofort, dass h = 5. 
Wir haben zum Beispiel 1 gesehen, dass h = -4. Um nun k zu finden, lösen wir diese Gleichung, indem wir diesen Wert von h in die Gleichung für die Variable x einsetzen: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Aus Beispiel 2 wissen wir, dass der Wert von k gleich 12 ist, ohne dass eine Berechnung erforderlich ist. 
In Beispiel 1 ist der obere Rand des Diagramms (-4,7). Zeichnen Sie den Punkt in Ihrem Diagramm und stellen Sie sicher, dass Sie die Koordinaten richtig benennen. In Beispiel 2 ist die Spitze (5,12). Also vom Punkt (0,0) gehst du 5 Stellen nach rechts und dann 12 nach oben. 
Im Fall von Beispiel 1 ist die Symmetrieachse die Linie parallel zur y-Achse und geht durch den Punkt (-4, 7). Obwohl es nicht Teil der Parabel selbst ist, kann Ihnen eine leichte Hervorhebung dieser Anleitung zeigen, wie symmetrisch die Kurve der Parabel ist. 
In Beispiel 1 haben wir es mit der Funktion (f(x) = 2x +16x + 39) zu tun, also eine Talparabel, denn a = 2 (positiv). In Beispiel 2 haben wir es mit der Funktion f(x) = 4(x - 5) + 12) zu tun, und dies ist auch eine Talparabel, da a = 4 (positiv). 
Bestimmen Sie f(x) = 0 und lösen Sie die Gleichung. Diese Methode kann für einfache quadratische Gleichungen funktionieren, insbesondere in der Scheitelpunktform, aber Sie werden feststellen, dass es immer schwieriger wird, wenn die Funktionen komplexer werden. Unten sind ein paar Beispiele. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/- 1 = x -12. x = 11 und 13 sind die Schnittpunkte mit der x-Achse der Parabel. Faktorisieren Sie die Gleichung. Einige Gleichungen der Form ax + bx + c können leicht umgeschrieben werden als (dx + e)(fx +g), wobei dx × fx = ax, (dx × g + fx × e) = bx und e × g = C. In diesem Fall sind die x-Achsenabschnitte die Werte von x, wobei jeder Term in den Klammern 0 wird. Zum Beispiel: x + 2x + 1 = (x + 1) (x + 1) In diesem Fall ist der Schnittpunkt gleich -1, denn wenn er mit beiden Faktoren ausgefüllt wird, ergibt sich null. Verwenden Sie die abc-Formel. Wenn es nicht einfach ist, die Schnittpunkte herauszufinden oder die Gleichung zu faktorisieren, verwenden Sie die "abc formel" was speziell dafür gedacht ist. Angenommen eine Gleichung in der Form ax + bx + c. Geben Sie dann die Werte von a, b und c in die Formel x = (-b +/- SqRt(b - 4ac))/2a . ein. Beachten Sie, dass dies oft zwei Antworten für x gibt, was in Ordnung ist - das bedeutet nur, dass Ihre Parabel zwei Schnittpunkte mit der x-Achse hat. Hier ist ein Beispiel: -Setze 5x + 1x + 10 wie folgt in die Gleichung ein: x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5) x = (-1 +/- SqRt(1 + 200))/-10 x = (-1 +/- SqRt(201))/-10 x = (-1 +/- 14,18)/-10 x = (13,18/-10) und (-15,18/-10). Die Schnittpunkte der Parabel mit der x-Achse betragen ungefähr x = -1.318 und 1.518 Wie in Beispiel 1 mit der Gleichung 2x + 16x + 39 sieht dies so aus: x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2) x = (-16 +/- SqRt(256 - 312))/4 x = (-16 +/- SqRt(-56)/-10 Da es nicht möglich ist, die Quadratwurzel einer negativen Zahl zu finden, wissen wir, dass es für diese spezielle Parabel keine Schnittpunkte mit der x-Achse gibt. 
Wir wissen zum Beispiel, dass unsere quadratische Gleichung 2x + 16x + 39 einen Schnittpunkt y = 39 hat, können diesen aber auch wie folgt ermitteln: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. Der Schnittpunkt der Parabel mit der y-Achse: y = 39. Wie oben angegeben, können wir den Schnittpunkt leicht ablesen, da y = c. Die Gleichung 4(x - 5) + 12 hat einen Schnittpunkt mit der y-Achse, der wie folgt gefunden werden kann: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. Der Schnittpunkt mit der y-Achse: y = 112. 
Schauen wir uns noch einmal die Gleichung x + 2x + 1 . an. Wir wissen bereits, dass der einzige Schnittpunkt mit der x-Achse (-1.0) ist. Da es an diesem Punkt nur tangential zur x-Achse ist, können wir folgern, dass die Ecke des Graphen gleich diesem Punkt ist. Bisher haben wir nur einen Punkt dieser Parabel – nicht annähernd genug, um einen Graphen zeichnen zu können. Lass uns noch ein paar Punkte finden, um sicherzustellen, dass wir mehr Werte haben. Versuchen wir, die y-Werte zu finden, die mit den folgenden x-Werten verbunden sind: 0, 1, -2 und -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Dann ist der Punkt (0,1). x=1: f(x) = (1) + 2(1) + 1 = 4. Dann ist der Punkt (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Dann ist der Punkt (-2.1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Dann ist der Punkt (-3.4). Platziere diese Punkte in der Grafik und zeichne deine Parabel. Beachten Sie, dass die Parabel völlig symmetrisch ist – wenn Sie die Punkte auf einer Seite des Graphen kennen, können Sie sich normalerweise viel Arbeit sparen, indem Sie diese Punkte verwenden, um die Punkte auf der anderen Seite der Symmetrieachse zu finden.
Eine funktion grafisch darstellen
Da ein Graph eine quadratische Gleichung sieht ax + bx + c, auch jede geschrieben alsa(x - h) + k, sieht aus wie eine glatte U-förmige Kurve. Das nennen wir a Parabel. Das Zeichnen einer quadratischen Gleichung beinhaltet das Finden des Scheitelpunkts, der Richtung und oft der Schnittpunkte mit der x-Achse und der y-Achse. Bei der relativ einfachen quadratischen Gleichung kann es auch ausreichen, eine Reihe von Werten für x einzugeben, um diese Punkte im Koordinatensystem anzuzeigen, wonach die Parabel gezeichnet werden kann. Fahren Sie mit Schritt 1 fort, um zu beginnen.
Schritte

1. Bestimmen Sie, welche Art von quadratischer Gleichung Sie haben. Dies kann auf zwei Arten geschrieben werden: die Standardnotation und die Vertex-Notation (eine andere Art, die Quadratwurzelformel zu schreiben). Sie können beide verwenden, um einen Graphen einer quadratischen Gleichung zu erstellen, aber dieser Vorgang ist in beiden Fällen etwas anders. Normalerweise werden Sie auf die Standardform stoßen, aber es schadet sicherlich nicht, beide Formen zu lernen. Die zwei Formen einer quadratischen Gleichung sind: Die Scheitelpunktform. Hier wird die quadratische Gleichung geschrieben als: f(x) = a(x - h) + k wobei a, h und k reelle Zahlen sind und a ungleich Null ist. Diese Form wird Scheitelpunkt genannt, weil sich h und k direkt auf den Scheitelpunkt Ihrer Parabel am Punkt (h, k) beziehen. Zwei Beispiele für Gleichungen in Scheitelpunktform sind f(x) = 9(x - 4) + 18 und -3(x - 5) + 1 Um einen Graphen dieser Gleichungen erstellen zu können, bestimmen wir zuerst die Spitze (h,k) des Graphen. In der Standardgleichung findet man dies über: h = -b/2a und k = f(h), während es bereits in Scheitelpunktform gegeben ist, da h und k in der Gleichung vorkommen.
- Die Standardform. Hier wird die quadratische Gleichung geschrieben als: f(x) = ax + bx + c wobei a, b und c reelle Zahlen sind und a ungleich Null ist.
- Zwei Beispiele für quadratische Standardgleichungen: f(x) = x + 2x + 1 und f(x) = 9x + 10x -8.

2. Bestimmen Sie Ihre Variablen. Um eine quadratische Gleichung zu lösen, ist es normalerweise notwendig, die Variablen a, b und c (oder a, h und k) zu bestimmen. Ein normales Problem liefert Ihnen eine quadratische Gleichung in der Standardform, aber die Vertex-Notation kann auch vorkommen.

3. Berechnen Sie h. In der Vertex-Notation ist der Wert von h bereits angegeben, aber in der Standard-Notation muss dieser Wert noch berechnet werden. Denken Sie daran, dass für die Standardgleichung h = -b/2a.

4. k . berechnen. Wie bei h ist k bereits für Gleichungen in der Scheitelpunktform bekannt. Denken Sie bei Gleichungen in Standardnotation daran, dass k = f(h). Mit anderen Worten, Sie können k finden, indem Sie jede Variable x durch den Wert von h . ersetzen.

5. Zeichnen Sie den oberen oder unteren Rand des Diagramms. Der Kamm oder Tal Ihrer Parabel ist der Punkt (h, k) - h steht für die x-Koordinate und k steht für die y-Koordinate. Der Kamm ist der Mittelpunkt Ihrer Parabel – der höchste oder niedrigste Punkt, der Kamm oder das Tal eines Graphen in Form von a "SIE" oder umgekehrt. Den Scheitelpunkt einer Parabel bestimmen zu können ist ein wesentlicher Bestandteil, um einen korrekten Graphen zeichnen zu können – oft ist das Ermitteln des Scheitelpunkts einer Parabel Teil einer mathematischen Aufgabe in der Schule.

6. Zeichnen Sie die Symmetrieachse der Parabel. Die Symmetrieachse einer Parabel ist die Linie, die die Figur in der Mitte schneidet und sie genau in zwei Hälften teilt. Eine Seite des Graphen wird entlang dieser Linie in die andere Seite des Graphen gespiegelt. Für quadratische Gleichungen der Form ax + bx + c oder a(x - h) + k ist diese Achse die Linie parallel zur y-Achse, die durch den Scheitelpunkt der Parabel geht.

7. Bestimmen Sie die Richtung der Parabel. Nachdem man herausgefunden hat, was die Spitze der Parabel ist, muss man wissen, ob es sich um eine Bergparabel oder eine Talparabel handelt, also ob die Öffnung unten oder oben ist. Zum Glück ist das ganz einfach. wenn "ein" positiv, dass Sie es mit einer Talparabel zu tun haben; ist "ein" negativ dann ist es eine Bergparabel (mit der Öffnung unten)

8. Bestimmen Sie ggf. die Schnittpunkte der Parabel. In mathematischen Aufgaben werden Sie oft gebeten, die Schnittpunkte der Parabel mit der x-Achse anzugeben (dies sind "Null", ein oder zwei Punkte, an denen die Parabel die x-Achse schneidet oder berührt). Auch wenn sie nicht angefordert werden, sind diese Punkte sehr wichtig, um eine genaue Grafik zeichnen zu können. Aber nicht alle Parabeln schneiden sich mit der x-Achse. Wenn es sich um eine Talparabel handelt und der Talpunkt oberhalb der x-Achse oder bei einer Bergparabel knapp unterhalb der x-Achse liegt, dann sind einfach keine Schnittpunkte zu finden. Verwenden Sie in diesem Fall eine der folgenden Methoden:

9. Bestimmen Sie ggf. den Schnittpunkt der Parabel mit der y-Achse. Es ist oft nicht notwendig, aber manchmal erforderlich, diesen Schnittpunkt zu finden, zum Beispiel für eine mathematische Aufgabe. Dies ist ziemlich einfach - setzen Sie den Wert von x auf 0 und lösen Sie die Gleichung nach f(x) oder y, wodurch Sie den y-Wert des Punktes erhalten, an dem sich die Parabel mit der y-Achse schneidet. Der Unterschied zu den Schnittpunkten durch die x-Achse besteht darin, dass es mit der y-Achse immer nur einen Schnittpunkt gibt. Hinweis – für Standardgleichungen liegt der Schnittpunkt mit der y-Achse bei y = c.

10. Wenn Sie dies für erforderlich halten, zeichnen Sie zuerst zusätzliche Punkte und dann den gesamten Graphen. Sie sollten jetzt einen Gipfel oder ein Tal, eine Richtung, Schnittpunkte mit der x-Achse und möglicherweise mit der y-Achse Ihrer Gleichung haben. Von diesem Punkt aus können Sie versuchen, die Parabel mit diesen Punkten zu zeichnen, oder Sie können versuchen, mehr Punkte zu finden, um die Grafik genauer zu machen. Der einfachste Weg, dies zu tun, besteht darin, einfach eine Reihe von x-Werten einzugeben, was eine Reihe von y-Werten zurückgibt. Sie werden oft (vom Lehrer) gebeten, zuerst eine Anzahl von Punkten zu berechnen, bevor Sie die Parabel zeichnen können.
Tipps
- Runden Sie Zahlen wenn nötig oder verwenden Sie Brüche. Dies kann helfen, eine Grafik korrekt anzuzeigen.
- Beachten Sie, dass, wenn für die Funktion f(x) = ax + bx + c, b oder c gleich Null sind, diese Terme verschwinden. Zum Beispiel ist 12x + 0x + 6 gleich 12x + 6, weil 0x gleich 0 . ist.
Оцените, пожалуйста статью