In Lehrbüchern und Tests werden rechte Winkel oft mit einem kleinen Quadrat in der rechten Ecke angegeben. Diese besondere Kennzeichnung bedeutet "90 Grad." 
Wenn Ihr Dreieck die Seiten 3 und 4 hat und Sie diesen Seiten Buchstaben zugewiesen haben, sodass a = 3 und b = 4 ist, berechnen Sie die Gleichung wie folgt: 3 + 4 = c. 
Wenn a = 3, a = 3 x 3 oder 9.Wenn b = 4, dann b = 4 x 4 oder 16. Wenn Sie diese Werte in Ihre Gleichung einbeziehen, sollte sie jetzt so aussehen: 9 + 16 = c. 
In unserem Beispiel, 9 + 16 = 25, dann beachte 25 = c. 
In unserem Beispiel, c = 25.Die Quadratwurzel von 25 ist 5 (5 x 5 = 25, So Quadrat(25) = 5).Und das heißt c = 5, die Länge unserer Hypotenuse! 

Sie berechnen die Hypotenuse dieses Dreiecks basierend auf der Länge eines der Beine und multiplizieren seine Länge mit Sqrt(2). Es ist hilfreich, dieses Verhältnis zu kennen, insbesondere wenn Sie bei Ihren Test- oder Hausaufgaben die Seitenlängen in Form von Variablen anstelle von ganzen Zahlen angeben. 
Bei gegebener Länge des kürzesten Beins (das dem 30-Grad-Winkel entgegengesetzte) multiplizieren Sie die Länge dieses Beins mit 2, um die Länge der Hypotenuse zu erhalten. Zum Beispiel, wenn die Länge des kürzesten Beins 4 ist, dann wissen Sie, dass die Hypotenuse 8 muss sein. Wenn Sie die Länge des längeren Beins kennen (entgegen dem 60-Grad-Winkel), multiplizieren Sie diese Länge mit2/Quadrat (3) um die Länge der Hypotenuse zu finden.Zum Beispiel, wenn die Länge des kürzesten Beins 4 ist, dann wissen Sie, dass die Hypotenuse 4.62 muss sein. 

Um den Sinus eines 80-Grad-Winkels zu finden, werden Sie Sünde 80 muss eingeben, gefolgt vom Gleichheitszeichen oder Enter, oder80 Sünde. (Die Antwort ist -0,9939.) Sie können auch nach suchen "Sündenrechner" mit Ihrem Browser für einige einfach zu bedienende Taschenrechner, damit Sie nicht raten müssen. 
Die Sinusregel kann tatsächlich verwendet werden, um nach aufzulösen jeder Dreieck, aber nur ein rechtwinkliges Dreieck hat eine Hypotenuse. 

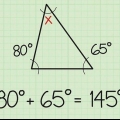
Zum Beispiel, wenn du das weißt A = 40 Grad, dann B = 180 – (90 + 40). Vereinfachen Sie dies zu B = 180 – 130 und das kannst du schnell ableiten B = 50 Grad. 
Um mit unserem Beispiel fortzufahren, nehmen wir an, dass die Länge der Seite a = 10.Winkel C = 90 Grad, Winkel A = 40 Grad und Winkel B = 50 Grad. 

Ausgehend von unserem Beispiel sehen wir das Sünde 40 = 0,64278761.Um den Wert von c zu finden, teilen wir die Länge von a durch diese Zahl und finden, dass 10 / 0,64278761 = 15,6, die Länge unserer Hypotenuse!
Bestimmung der länge der hypotenuse
Alle rechtwinkligen Dreiecke haben einen rechten Winkel (von 90 Grad), und die Hypotenuse ist die diesem Winkel gegenüberliegende Seite. Die Hypotenuse ist die längste Seite des Dreiecks und lässt sich mit verschiedenen Methoden auch sehr leicht finden. In diesem Artikel erfahren Sie, wie Sie die Länge der Hypotenuse mit dem Satz des Pythagoras bestimmen, vorausgesetzt, Sie kennen die Länge der anderen beiden Seiten des Dreiecks. Dann lernst du, wie man die Hypotenuse einiger spezieller rechtwinkliger Dreiecke berechnet, die dir oft in Tests begegnen. Und schließlich lernen Sie, die Länge der Hypotenuse nach der Sinusregel zu berechnen, wenn nur die Länge einer der Seiten bekannt ist und der Betrag eines der Winkel.
Schritte
Methode 1 von 3: Verwenden des Satzes des Pythagoras

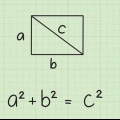
1. Lerne den Satz des Pythagoras. Der Satz des Pythagoras beschreibt die Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks. Sie besagt, dass für ein beliebiges rechtwinkliges Dreieck mit den Seiten a und b und einer Hypotenuse der Länge c gilt a + b = c.

2. Stellen Sie sicher, dass Ihr Dreieck ein rechtwinkliges Dreieck ist.Der Satz des Pythagoras funktioniert nur für rechtwinklige Dreiecke, und per Definition kann nur ein rechtwinkliges Dreieck eine Hypotenuse haben.Wenn Ihr Dreieck einen Winkel von genau 90 Grad enthält, ist es ein rechtwinkliges Dreieck und Sie können fortfahren.

3. Weisen Sie den Seiten Ihres Dreiecks die Variablen a, b und c zu.Die Variable "C" wird immer der Hypotenuse zugeordnet, also der längsten Seite.Wählen Sie eine der anderen Seiten für die ein, und benenne die verbleibende Seite B (egal welche, die Mathematik bleibt die gleiche).Verarbeiten Sie dann die Längen von a und b in die Formel, wie im folgenden Beispiel gezeigt:

4. Bestimme die Quadrate von a und b.Um das Quadrat einer Zahl zu finden, multipliziere diese Zahl einfach mit sich selbst, also a = a x a. Finde die Quadrate von a und b und füge sie in die Formel ein.

5. Zähle die Werte vonein und B zusammen auf. Berücksichtigen Sie dies in Ihrer Gleichung und Sie erhalten den Wert von c. Jetzt fehlt nur noch ein Schritt und Sie haben die Hypotenuse bestimmt!

6. Bestimme die Quadratwurzel von c. Verwenden Sie die Quadratwurzelfunktion Ihres Taschenrechners (oder Multiplikationstabellen, wenn Sie sie auswendig kennen), um die Quadratwurzel von c . zu finden. Die Antwort ist die Länge Ihrer Hypotenuse!
Methode 2 von 3: Bestimmung der Hypotenuse spezieller rechtwinkliger Dreiecke

1. Lerne die Dreiecke eines pythagoräischen Dreiers zu erkennen. Die Längen der Seiten einer pythagoräischen Triade sind ganze Zahlen, die dem Satz des Pythagoras gehorchen. Diese speziellen Dreiecke werden Ihnen regelmäßig in Geometrielehrbüchern und in Standardtests wie dem SAT und dem GRE begegnen.Insbesondere, wenn Sie sich die ersten 2 pythagoräischen Tripel merken, können Sie sich bei diesen Tests viel Zeit sparen, da Sie die Hypotenuse jedes dieser Dreiecke sofort kennen, indem Sie sich nur die Längen der Seiten ansehen!
- Das erste pythagoräische Trio ist 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Wenn Sie ein rechtwinkliges Dreieck mit den Seitenlängen 3 und 4 sehen, wissen Sie sofort, dass die Hypotenuse 5 beträgt, ohne dass Sie irgendwelche Berechnungen durchführen müssen.
- Das Verhältnis eines pythagoräischen Tripels bleibt auch dann gleich, wenn die Seiten mit einer anderen Zahl multipliziert werden. Zum Beispiel: ein rechtwinkliges Dreieck mit Seiten 6 und 8 wird eine Hypotenuse von haben 10 (6 + 8 = 10, 36 + 64 = 100).Das gleiche gilt für9-12-15, auch 1,5-2-2,5.Mach die Berechnungen und du wirst sehen!
- Das zweite pythagoräische Trio, das Ihnen in Tests häufig begegnet, ist 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Achten Sie auch auf seine Pluralformen, wie z 10-24-26 und 2,5-6-6,5.

2. Lernen Sie das Seitenverhältnis eines rechtwinkligen Dreiecks mit den Winkeln 45-45-90. Ein rechtwinkliges 45-45-90-Dreieck hat Winkel von 45, 45 und 90 Grad und wird auch als gleichschenkliges rechtwinkliges Dreieck bezeichnet. Dieses Dreieck wird häufig bei Standardtests gefunden und ist ein sehr einfach zu lösendes Dreieck. Das Seitenverhältnis dieses Dreiecks ist 1:1:Quadrat(2), was bedeutet, dass die Länge der Beine gleich ist, und die Länge der Hypotenuse ist dann einfach die Länge der Beine multipliziert mit der Quadratwurzel aus zwei.

3. Lernen Sie die Proportionen eines rechtwinkligen 30-60-90-Dreiecks. Dieses Dreieck hat Winkel von 30, 60 und 90 Grad und kann hergestellt werden, indem ein gleichseitiges Dreieck in zwei Hälften geteilt wird. Die Seiten des rechtwinkligen Dreiecks 30-60-90 haben immer das Verhältnis 1:Quadrat(3):2, oder x:Quadrat(3)x:2x.Wenn man die Länge eines Beins des rechten 30-60-90-Dreiecks angibt und nach der Hypotenuse fragt, ist dies sehr einfach:
Methode 3 von 3: Berechnung der Hypotenuse mit der Sinusregel

1. Verstehen Sie, was die "Sinus" bedeutet. Die Bedingungen "Sinus," "Kosinus" und "Tangente" alle beziehen sich auf bestimmte Proportionen zwischen den Winkeln und/oder Seiten eines rechtwinkligen Dreiecks.In einem rechtwinkligen Dreieck ist die is Sinus eines Winkels definiert als die Länge der dem Winkel gegenüberliegenden Seite geteilt durch die Hypotenuse des Dreiecks. Die Abkürzung für Sinus, wie sie auf Ihrem Taschenrechner erscheint, ist Sünde.

2. Erfahren Sie, wie Sie den Sinus berechnen. Sogar ein einfacher wissenschaftlicher Taschenrechner hat eine Sinusfunktion. Schau dir den markierten Schlüssel an Sünde.Um den Sinus eines Winkels zu ermitteln, drücken Sie normalerweise die Sünde-Geben Sie dann den Winkel in Grad ein.Bei einigen Taschenrechnern müssen Sie jedoch zuerst den Winkel in Grad eingeben und dann die Taste . drücken Sünde-Knopf drücken. Sie müssen mit Ihrem Taschenrechner experimentieren oder im Handbuch nachschauen, um herauszufinden, welcher es ist.

3. Lerne die Sinusregel.Die Sinusregel ist ein nützliches Werkzeug zum Lösen von Dreiecksproblemen. Sie können es hauptsächlich verwenden, um die Hypotenuse eines rechtwinkligen Dreiecks zu finden, wenn Sie die Länge einer Seite und einen anderen seiner Winkel als den rechten Winkel kennen. Für jedes Dreieck mit Seiten ein, B und C und die Ecken ein, B und C, die Sinusregel besagt, dass ein / Sünde ein = B / Sünde B = C / Sünde C.

4. Weisen Sie den Seiten Ihres Dreiecks die Variablen a, b und c zu. Die Hypotenuse (die längste Seite) sollte immer die "C" sind. Beschriften Sie der Einfachheit halber die Seite bekannter Länge als "ein" und andere "B". Weisen Sie dann den Ecken des Dreiecks die Variablen A, B und C zu. Der rechte Winkel gegenüber der Hypotenuse wird dann "C".Die Ecke gegenüber "ein" ist Winkel "ein" und der Winkel gegenüberliegende Seite "B" ist "B".

5. Berechnen Sie den dritten Winkel. Weil es ein rechter Winkel ist, weißt du das schon C = 90 Grad und du weißt auch welchen winkel ein oder B ist. Da die Summe aller Winkel in einem Dreieck immer 180 Grad betragen muss, lässt sich der dritte Winkel leicht nach folgender Formel berechnen: 180 – (90 + A) = B. Sie können diese Gleichung auch umkehren, sodass 180 – (90 + B) = A.

6. Untersuche dein Dreieck.Zu diesem Zeitpunkt kennen Sie alle Winkel des Dreiecks und die Seitenlänge a. Jetzt ist es an der Zeit, diese Werte in die Sinusregel zu verarbeiten, um die Länge der anderen beiden Seiten zu berechnen.

7. Wende die Sinusregel auf dein Dreieck an.Wir müssen nur unsere Zahlen verarbeiten und die folgende Gleichung lösen, um die Länge der Hypotenuse c zu finden: Seitenlänge a / Sünde A = Seitenlänge c / Sünde C.Dies mag immer noch etwas einschüchternd aussehen, aber der 90-Grad-Sinus ist eine Konstante und entspricht immer 1!Unsere Gleichung kann daher vereinfacht werden zu: ein / Sünde A = c / 1, oder einfacher ein / Sünde A = c.

8. Teilen Sie die Länge der Seideein durch den Sinus des Winkels ein um die Länge der Hypotenuse zu finden!Sie können dies in zwei separaten Schritten berechnen, indem Sie zunächst: Sünde Berechne und schreibe A, dann dividiere durch a. Oder testen Sie alles auf einmal in Ihrem Taschenrechner. Vergessen Sie dabei nicht die Klammern nach dem Divisionszeichen.Geben Sie zum Beispiel ein 10 / (Sünde 40) oder 10 / (40 Sünde), je nach Rechner.
"Bestimmung der länge der hypotenuse"
Оцените, пожалуйста статью