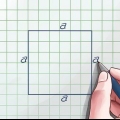
Wenn beispielsweise die Breite eines Rechtecks 3 cm und die Länge 4 cm beträgt, würde Ihre Formel so aussehen:  .
. 
Zum Beispiel:




Zum Beispiel:



Die Diagonale oder ein Rechteck mit einer Breite von 3 cm und einer Länge von 4 cm beträgt also 5 cm. 

Wenn die Fläche des Rechtecks beispielsweise 35 Quadratzentimeter beträgt, würde Ihre Formel so aussehen:  .
. 
Zum Beispiel:

 .
. 

Wenn der Umfang eines Rechtecks beispielsweise 24 Zentimeter beträgt, würde Ihre Formel so aussehen:  .
. 
Zum Beispiel:


 .
. 
Wenn Sie beispielsweise mit der Flächenformel gefunden haben, dass  , dann ersetzt du den Wert
, dann ersetzt du den Wert  in der Umfangsformel:
in der Umfangsformel:



Zum Beispiel:




Zum Beispiel:




Zum Beispiel,  wird
wird  .
. 
Zum Beispiel die Gleichung  kann aufgelöst werden in
kann aufgelöst werden in  .
. 
Zum Beispiel:


UND

 .
.
Die Länge und Breite des Rechtecks betragen also 7 cm und 5 cm. 
Sie verwenden den Satz des Pythagoras, weil die Diagonale eines Rechtecks es in zwei kongruente rechtwinklige Dreiecke teilt. Die Breite und Länge des Rechtecks sind die Längen der Seiten des Dreiecks; die Diagonale ist die Hypotenuse des Dreiecks. 
Wenn Sie beispielsweise wissen, dass die Breite und Länge des Rechtecks 5 cm und 7 cm betragen, würde Ihre Formel so aussehen:  .
. 
Zum Beispiel:




Zum Beispiel:



Die Diagonale eines Rechtecks mit einer Fläche von 35 cm und einem Umfang von 24 cm beträgt also etwa 8,6 cm. 

Sie können diese Methode verwenden, wenn Sie den Umfang des Rechtecks kennen, außer dass Sie jetzt die Umfangsformel anstelle der Flächenformel verwenden. Die Formel für den Umfang eines Rechtecks lautet  , wodurch
, wodurch  gleich der Breite des Rechtecks und
gleich der Breite des Rechtecks und  ist gleich der Länge des Rechtecks.
ist gleich der Länge des Rechtecks. 
Wenn die Fläche des Rechtecks beispielsweise 35 Quadratzentimeter beträgt, würde Ihre Formel wie Volt aussehen:  .
. 
Zum Beispiel, wenn Sie das gefunden haben  , dann ersetzen Sie diese Beziehung für
, dann ersetzen Sie diese Beziehung für  in der Flächenformel:
in der Flächenformel:



Zum Beispiel:




Zum Beispiel die Gleichung  kann aufgelöst werden als
kann aufgelöst werden als  .
. 
Zum Beispiel:


UND

 .
.
In diesem Fall gibt es eine negative Antwort. Da die Länge eines Rechtecks nicht negativ sein kann, wissen Sie, dass die Länge 5 cm betragen muss. 
Wenn Sie beispielsweise wissen, dass die Länge des Rechtecks 5 cm beträgt und die Beziehung zwischen den Seitenlängen  , dann gibst du 5 als Länge in die Formel ein:
, dann gibst du 5 als Länge in die Formel ein:




Sie verwenden den Satz des Pythagoras, weil die Diagonale eines Rechtecks es in zwei kongruente rechtwinklige Dreiecke teilt. Die Breite und Länge des Rechtecks sind die Längen der Seiten des Dreiecks; die Diagonale ist die Hypotenuse des Dreiecks. 
Wenn Sie beispielsweise wissen, dass Breite und Länge des Rechtecks 5 cm und 7 cm betragen, sieht Ihre Formel jetzt so aus:  .
. 
Zum Beispiel:




Zum Beispiel:



Die Diagonale eines Rechtecks mit einer Breite von 2 cm über seiner Länge und einer Fläche von 35 cm beträgt also etwa 8,6 cm.
Berechnen sie die länge der diagonale in einem rechteck
Eine Diagonale ist eine gerade Linie, die eine Ecke eines Rechtecks mit der gegenüberliegenden Ecke verbindet. Ein Rechteck hat zwei gleich lange Diagonalen. Wenn Sie die Seitenlängen eines Rechtecks kennen, können Sie die Länge der Diagonalen mit dem Satz des Pythagoras leicht ermitteln, da eine Diagonale ein Rechteck in zwei rechtwinklige Dreiecke teilt. Wenn Sie die Seitenlängen nicht kennen, aber andere Daten haben (z. B. die Fläche und den Umfang oder das Verhältnis zwischen den Seitenlängen), können Sie die Länge und Breite der Seiten mit a . messen einige zusätzliche Schritte, finde das Rechteck und bestimme dann mit dem Satz des Pythagoras die Länge und Breite der Diagonale.
Schritte
Methode 1 von 3: Verwenden der Länge und Breite

1. Schreiben Sie die Formel für den Satz des Pythagoras. Die Formel lautet  , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
 , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks. - Sie verwenden den Satz des Pythagoras, weil die Diagonale eines Rechtecks es in zwei kongruente rechtwinklige Dreiecke teilt. Die Länge und Breite des Rechtecks sind die Längen der Seiten des Dreiecks; die Diagonale ist die Hypotenuse des Dreiecks.

2. Wenden Sie die Länge und Breite auf die Formel an. Diese sind, wenn es richtig gegeben ist, oder Sie können sie messen. Stellen Sie sicher, dass Sie für ersetzen  und
und  .
.
 und
und  .
. .
.
3. Quadrieren Sie Länge und Breite und addieren Sie diese Zahlen zusammen. Beim Quadrieren wird die Zahl mit sich selbst multipliziert.




4. Subtrahiere die Quadratwurzel jeder Seite der Gleichung. Der einfachste Weg, eine Quadratwurzel zu finden, ist die Verwendung eines Taschenrechners. Sie können einen Online-Rechner verwenden, wenn Sie keinen wissenschaftlichen Taschenrechner haben. Dies gibt Ihnen den Wert  , oder die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
, oder die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
 , oder die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
, oder die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.


Die Diagonale oder ein Rechteck mit einer Breite von 3 cm und einer Länge von 4 cm beträgt also 5 cm.
Methode 2 von 3: Verwenden der Fläche und des Umfangs

1. Schreiben Sie die Formel für die Fläche eines Rechtecks. Die Formel lautet  , wodurch
, wodurch  ist gleich der Fläche des Rechtecks,
ist gleich der Fläche des Rechtecks,  gleich der Länge des Rechtecks und
gleich der Länge des Rechtecks und  gleich der Breite des Rechtecks.
gleich der Breite des Rechtecks.
 , wodurch
, wodurch  ist gleich der Fläche des Rechtecks,
ist gleich der Fläche des Rechtecks,  gleich der Länge des Rechtecks und
gleich der Länge des Rechtecks und  gleich der Breite des Rechtecks.
gleich der Breite des Rechtecks.
2. Verwenden Sie die Fläche des Rechtecks in der Formel. Stellen Sie sicher, dass Sie die richtige Variable ersetzen  .
.
 .
. .
.
3. Ordnen Sie die Formel um, und Sie erhalten einen Wert für w  . Sie tun dies, indem Sie beide Seiten der Gleichung durch dividieren
. Sie tun dies, indem Sie beide Seiten der Gleichung durch dividieren  . Legen Sie diesen Wert beiseite. Sie werden dies später in der Formel für den Umfang verwenden.
. Legen Sie diesen Wert beiseite. Sie werden dies später in der Formel für den Umfang verwenden.
 . Sie tun dies, indem Sie beide Seiten der Gleichung durch dividieren
. Sie tun dies, indem Sie beide Seiten der Gleichung durch dividieren  . Legen Sie diesen Wert beiseite. Sie werden dies später in der Formel für den Umfang verwenden.
. Legen Sie diesen Wert beiseite. Sie werden dies später in der Formel für den Umfang verwenden.
 .
.
4. Schreiben Sie die Formel für den Umfang eines Rechtecks. Die Formel lautet  , wodurch
, wodurch  gleich der Breite des Rechtecks und
gleich der Breite des Rechtecks und  ist gleich der Länge des Rechtecks.
ist gleich der Länge des Rechtecks.
 , wodurch
, wodurch  gleich der Breite des Rechtecks und
gleich der Breite des Rechtecks und  ist gleich der Länge des Rechtecks.
ist gleich der Länge des Rechtecks.
5. Verwenden Sie den Wert des Umfangs in der Formel. Stellen Sie sicher, dass Sie die Variable ersetzen  .
.
 .
. .
.
6. Teilen Sie beide Seiten der Gleichung durch 2. Dies gibt Ihnen den Wert  .
.
 .
.

 .
.
7. Verwenden Sie den Wert w  in der Gleichung. Verwenden Sie den gefundenen Wert, indem Sie die Flächenformel neu anordnen.
in der Gleichung. Verwenden Sie den gefundenen Wert, indem Sie die Flächenformel neu anordnen.
 in der Gleichung. Verwenden Sie den gefundenen Wert, indem Sie die Flächenformel neu anordnen.
in der Gleichung. Verwenden Sie den gefundenen Wert, indem Sie die Flächenformel neu anordnen. , dann ersetzt du den Wert
, dann ersetzt du den Wert  in der Umfangsformel:
in der Umfangsformel:


8. Eliminiere den Bruch in der Gleichung. Sie tun dies, indem Sie beide Seiten der Gleichung mit multiplizieren  .
.
 .
.



9. Setze die Gleichung gleich 0. Sie tun dies, indem Sie den Term ersten Grades von beiden Seiten der Gleichung subtrahieren.




10. Ordne die Reihenfolge der Terme in der Gleichung um. Das bedeutet, dass zuerst der Term mit dem Exponenten kommt, dann der Term mit der Variablen und zuletzt die Konstante. Achte beim Umstellen auf die richtigen positiven und negativen Vorzeichen. Die Gleichung ist nun als quadratische Gleichung geordnet.
 wird
wird  .
.
11. Faktorisieren Sie die quadratische Gleichung. Eine detaillierte Anleitung dazu finden Sie im Artikel Quadratische Gleichungen lösen.
 kann aufgelöst werden in
kann aufgelöst werden in  .
.
12. Bestimmen Sie die Werte von l  . Sie tun dies, indem Sie jeden Term auf Null setzen und nach der Variablen auflösen. Sie erhalten zwei Lösungen für diese Gleichung. Da Sie es mit einem Rechteck zu tun haben, sind die beiden Lösungen die Breite und Länge Ihres Rechtecks.
. Sie tun dies, indem Sie jeden Term auf Null setzen und nach der Variablen auflösen. Sie erhalten zwei Lösungen für diese Gleichung. Da Sie es mit einem Rechteck zu tun haben, sind die beiden Lösungen die Breite und Länge Ihres Rechtecks.
 . Sie tun dies, indem Sie jeden Term auf Null setzen und nach der Variablen auflösen. Sie erhalten zwei Lösungen für diese Gleichung. Da Sie es mit einem Rechteck zu tun haben, sind die beiden Lösungen die Breite und Länge Ihres Rechtecks.
. Sie tun dies, indem Sie jeden Term auf Null setzen und nach der Variablen auflösen. Sie erhalten zwei Lösungen für diese Gleichung. Da Sie es mit einem Rechteck zu tun haben, sind die beiden Lösungen die Breite und Länge Ihres Rechtecks.

UND

 .
.Die Länge und Breite des Rechtecks betragen also 7 cm und 5 cm.

13. Schreiben Sie die Formel für den Satz des Pythagoras. Die Formel lautet  , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
 , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
14. Verwenden Sie den Breiten- und Längengrad in der Formel. Es spielt keine Rolle, welchen Wert Sie für welche Variable verwenden.
 .
.
fünfzehn. Quadrieren Sie den Breiten- und Längengrad und addieren Sie diese Zahlen dann zusammen. Quadrieren bedeutet, eine Zahl mit sich selbst zu multiplizieren.




16. Ziehe die Quadratwurzel jeder Seite der Gleichung. Der einfachste Weg, eine Quadratwurzel zu finden, ist die Verwendung eines Taschenrechners. Sie können einen Online-Rechner verwenden, wenn Sie keinen wissenschaftlichen Taschenrechner haben. Dies gibt Ihnen den Wert  , und das ist die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
, und das ist die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
 , und das ist die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.
, und das ist die Hypotenuse des Dreiecks und die Diagonale des Rechtecks.


Die Diagonale eines Rechtecks mit einer Fläche von 35 cm und einem Umfang von 24 cm beträgt also etwa 8,6 cm.
Methode 3 von 3: Verwenden der Fläche und der relativen Längen der Seiten

1. Schreiben Sie eine Formel, die die Beziehung zwischen den Längen der Seiten erklärt. Sie können die Länge ändern ( ) oder die Breite (
) oder die Breite ( ) isolieren. Legen Sie diese Formel für einen Moment beiseite. Sie werden es bald in der Oberflächenformel verwenden.
) isolieren. Legen Sie diese Formel für einen Moment beiseite. Sie werden es bald in der Oberflächenformel verwenden.
 ) oder die Breite (
) oder die Breite ( ) isolieren. Legen Sie diese Formel für einen Moment beiseite. Sie werden es bald in der Oberflächenformel verwenden.
) isolieren. Legen Sie diese Formel für einen Moment beiseite. Sie werden es bald in der Oberflächenformel verwenden. - Wenn Sie beispielsweise wissen, dass die Breite eines Rechtecks 2 cm mehr als seine Länge beträgt, können Sie eine Formel schreiben wie
:
.

2. Schreiben Sie die Formel für die Fläche eines Rechtecks. Die Formel lautet  , wodurch
, wodurch  ist gleich der Fläche des Rechtecks,
ist gleich der Fläche des Rechtecks,  gleich der Länge des Rechtecks und
gleich der Länge des Rechtecks und  gleich der Breite des Rechtecks.
gleich der Breite des Rechtecks.
 , wodurch
, wodurch  ist gleich der Fläche des Rechtecks,
ist gleich der Fläche des Rechtecks,  gleich der Länge des Rechtecks und
gleich der Länge des Rechtecks und  gleich der Breite des Rechtecks.
gleich der Breite des Rechtecks. , wodurch
, wodurch  gleich der Breite des Rechtecks und
gleich der Breite des Rechtecks und  ist gleich der Länge des Rechtecks.
ist gleich der Länge des Rechtecks.
3. Verwenden Sie die Fläche des Rechtecks in der Formel. Stellen Sie sicher, dass Sie die Variable ersetzen  .
.
 .
. .
.
4. Verwenden Sie die relationale Formel für die Länge (oder Breite) in der Formel. Da Sie es mit einem Rechteck zu tun haben, spielt es keine Rolle, ob Sie mit Variablen arbeiten  oder
oder  .
.
 oder
oder  .
. , dann ersetzen Sie diese Beziehung für
, dann ersetzen Sie diese Beziehung für  in der Flächenformel:
in der Flächenformel:


5. Machen Sie daraus eine quadratische Gleichung. Sie tun dies, indem Sie die Verteilungseigenschaft verwenden und die Terme in Klammern miteinander multiplizieren, wonach Sie die Gleichung gleich 0 . setzen.




6. Faktorisieren Sie die quadratische Gleichung. Eine detaillierte Anleitung dazu finden Sie im Artikel Quadratische Gleichungen lösen.
 kann aufgelöst werden als
kann aufgelöst werden als  .
.
7. Bestimmen Sie die Werte von l  . Sie tun dies, indem Sie jeden Term gleich Null machen und nach der Variablen auflösen. Du findest zwei Lösungen der Gleichung.
. Sie tun dies, indem Sie jeden Term gleich Null machen und nach der Variablen auflösen. Du findest zwei Lösungen der Gleichung.
 . Sie tun dies, indem Sie jeden Term gleich Null machen und nach der Variablen auflösen. Du findest zwei Lösungen der Gleichung.
. Sie tun dies, indem Sie jeden Term gleich Null machen und nach der Variablen auflösen. Du findest zwei Lösungen der Gleichung.

UND

 .
.In diesem Fall gibt es eine negative Antwort. Da die Länge eines Rechtecks nicht negativ sein kann, wissen Sie, dass die Länge 5 cm betragen muss.

8. Verwenden Sie den Wert der Länge (oder Breite) in Ihrer Beziehungsformel. Dadurch erhalten Sie die Länge der anderen Seite des Rechtecks.
 , dann gibst du 5 als Länge in die Formel ein:
, dann gibst du 5 als Länge in die Formel ein:



9. Schreiben Sie die Formel für den Satz des Pythagoras. Die Formel lautet  , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
 , wodurch
, wodurch  und
und  gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und
gleich den Seitenlängen eines rechtwinkligen Dreiecks sind und  gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
gleich der Länge der Hypotenuse eines rechtwinkligen Dreiecks.
10. Verwenden Sie den Breiten- und Längengrad in der Formel. Es spielt keine Rolle, welchen Wert Sie für welche Variable verwenden.
 .
.
11. Quadrieren Sie den Breiten- und Längengrad und addieren Sie diese Zahlen dann zusammen. Quadrieren bedeutet, eine Zahl mit sich selbst zu multiplizieren.




12. Subtrahiere die Quadratwurzel jeder Seite der Gleichung. Der einfachste Weg, eine Quadratwurzel zu finden, ist die Verwendung eines Taschenrechners. Sie können einen Online-Rechner verwenden, wenn Sie keinen wissenschaftlichen Taschenrechner haben. Dies gibt Ihnen den Wert  , oder die Hypotenuse des Dreiecks und damit die Diagonale des Rechtecks.
, oder die Hypotenuse des Dreiecks und damit die Diagonale des Rechtecks.
 , oder die Hypotenuse des Dreiecks und damit die Diagonale des Rechtecks.
, oder die Hypotenuse des Dreiecks und damit die Diagonale des Rechtecks.


Die Diagonale eines Rechtecks mit einer Breite von 2 cm über seiner Länge und einer Fläche von 35 cm beträgt also etwa 8,6 cm.
"Berechnen sie die länge der diagonale in einem rechteck"
Оцените, пожалуйста статью