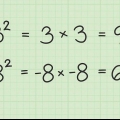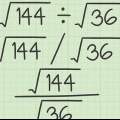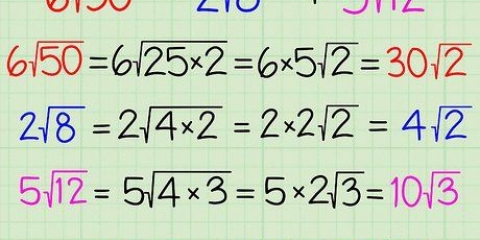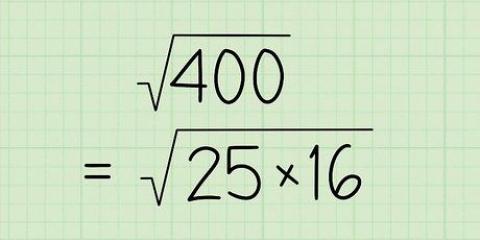Quadratwurzeln vereinfachen
Eine Quadratwurzel zu vereinfachen ist nicht so schwierig, wie es scheint. Um eine Quadratwurzel zu vereinfachen, müssen Sie nur die Zahl der Quadratwurzel faktorisieren und versuchen, die Quadratwurzel aus einem oder beiden Faktoren zu ziehen. Sobald Sie einige gängige Quadratzahlen kennen und wissen, wie man eine Zahl in Faktoren aufteilt, sind Sie auf dem besten Weg, eine Quadratwurzel zu vereinfachen. So lernst du das schnell.
Schritte
Methode 1 von 4: Vereinfachen der Quadratwurzel einer Zahl

1. Lerne einige Quadratzahlen und ihre Wurzeln. Quadrieren, Multiplizieren einer Zahl mit sich selbst, ergibt eine quadrierte Zahl (perfekt quadratisch). Zum Beispiel: 25 ist eine Zahl im Quadrat, weil 5 x 5 oder 5 gleich 25 . ist. Wenn Sie mindestens die ersten 10 bis 10 Quadratzahlen kennen, können Sie Quadratwurzeln erkennen und vereinfachen. Hier sind die ersten zehn quadrierten Zahlen:
- 1 = 1
- 2 = 4
- 3 = 9
- 4 = 16
- 5 = 25
- 6 = 36
- 7 = 49
- 8 = 64
- 9 = 81
- 10 = 100

2. Finden Sie die Quadratwurzel einer Quadratzahl. Wenn Sie eine Quadratzahl unter einem Radikal sehen, müssen Sie nur das Radikal (√ ) entfernen und die Quadratwurzel der Quadratzahl schreiben. Wenn du das schon auswendig gelernt hast, dann bist du fertig. Wenn die Zahl zu groß ist und Sie sich nicht sicher sind, ob es sich um eine Quadratzahl handelt, versuchen Sie mit Ihrem Taschenrechner die Quadratwurzel zu finden, um zu überprüfen, ob sie eine schöne runde Zahl ergibt. Zum Beispiel: bei √25 wissen Sie, dass die Antwort gleich 5 ist, weil 25 eine Zahl im Quadrat ist.
Methode 2 von 4: Vereinfachen einer Quadratwurzel durch Faktorisieren

1. Wenn die Zahl gerade ist, dividiere sie durch 2. Um die Faktoren einer Zahl zu finden, müssen alle Zahlen gefunden werden, die miteinander multipliziert diese Zahl ergeben, was es einfacher macht, ihre Quadratwurzel zu bestimmen. Wenn es eine gerade Zahl ist, können Sie die Zahl als erstes durch 2 teilen. In diesem Beispiel können Sie √98 in √(2x49) teilen, denn 98 : 2 =49. Wenn die Zahl nicht durch 2 teilbar ist, versuchen Sie es mit 3, 4, 5 usw., bis Sie die richtige Kombination gefunden haben.

2. Teile diese Faktoren wieder in Faktoren auf, um weitere Quadratzahlen zu finden. Sehen Sie, ob Sie die Zahl weiterhin in Faktoren aufteilen können. 2 ist prim und hat nur sich selbst und 1 als Teiler. Aber 49, der andere Faktor, kann immer noch in 7 x 7 geteilt werden, weil es eine Quadratzahl ist. Sie können also die Wurzel √(2x49) umschreiben als √(2x7x7), oder √[2(7)], was bedeutet, dass wir die gesuchte Quadratzahl bereits gefunden haben.

3. Vereinfachen Sie die Quadratwurzel. Wegen √98= √[2(7)] ist es möglich, a 7 außerhalb des Radikals zu platzieren und die Antwort auf 7√2 . zu vereinfachen. Also √49 oder auch (7 x 7) wird dann 7, sobald du es außerhalb des Radikals platzierst. Legt man die 7 wieder zurück, wird sie wieder zu einer Quadratzahl und damit 49. Also, √98 = 7√2.
Methode 3 von 4: Andere Methoden zur Vereinfachung einer Quadratwurzel
1. Wenn es Ihnen nicht auf Anhieb gelingt, eine Quadratzahl zu finden, teilen Sie die Zahl weiter. Wenn das Problem beispielsweise √48 ist, dividieren Sie weiter, bis Sie 2x2 nicht überschreiten können, sodass 4 ein Koeffizient des Radikals wird und 3 innerhalb des Radikals bleibt. So funktioniert das:
- √48 = √(2 x 24)
- (2 x 24) = √(2 x 12 x 2)
- (2 x 12 x 2) = √(2 x 6 x 2 x 2)
- (2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
- (2 x 3 x 2 x 2 x 2) = √(2 x 3)
- √(2 x 3)= 4√3
- √48 = 4√3
2. Denken Sie daran, dass Sie eine Primzahl nicht vereinfachen können. Das liegt daran, dass die Faktoren hier 1 und die Primzahl selbst sind. Zum Beispiel: √17 kann nicht vereinfacht werden, weil 17 eine Primzahl ist.
3. Aufteilen in Faktoren von mehr als einer Quadratzahl. Wenn die Faktoren der Zahl mehr als eine Quadratzahl enthalten, nehmen Sie sie alle außerhalb des Radikals. Wenn Sie beim Vereinfachen mehrere Quadrate gefunden haben, nehmen Sie sie alle außerhalb des Radikals und multiplizieren Sie sie. Zum Beispiel: Nehmen wir an, Sie möchten die Zahl √32 vereinfachen, dann teilen Sie sie in die Faktoren 4 x 4 x 2 und beachten Sie, dass die Quadratzahl 4 zweimal vorkommt. Machen Sie dieses 16√2, was schließlich 4√2 . ergibt.
4. Verwechseln Sie den Koeffizienten nicht mit einer höheren Potenzwurzel. 3√125 ist zum Beispiel gleich 3 x √125, aber √125 ist die Kubikwurzel von 125. (weil 5 x 5 x 5 = 125, √125 = 5.)
Methode 4 von 4: Die Terminologie kennen

1. Denken Sie daran, dass das Radikal (√) das Symbol für die Quadratwurzel ist. Zum Beispiel in der Aufgabe √25, "√" das radikale zeichen.

2. Denken Sie daran, dass das Radikal die Zahl unter dem Radikal ist. Finden Sie die Quadratwurzel dieser Zahl. Zum Beispiel: bei √25 ist "25" die Wurzelzahl.

3. Denken Sie daran, dass der Koeffizient die Zahl außerhalb des Radikals ist. Diese Zahl multipliziert die Quadratwurzel; Dieses findet sich links neben dem Wurzelzeichen, dem √-Symbol. Zum Beispiel: bei 7√2, "7" der Koeffizient.

4. Denken Sie daran, dass ein Faktor eine Zahl ist, die vollständig in eine andere Zahl eingeht. Zum Beispiel: 2 ist ein Faktor von 8, weil 8 ÷ 4 = 2, aber 3 ist kein Faktor von 8, weil 8÷3 keine ganze Zahl antwortet. Zum Beispiel: 5 ist ein Faktor von 25, weil 5 x 5 = 25.

5. Verstehen Sie die Bedeutung der Vereinfachung einer Quadratwurzel. Das Vereinfachen einer Quadratwurzel besteht einfach darin, ein Quadrat einer Quadratwurzel in Faktoren zu unterteilen, es dann nach links vom Radikal zu verschieben und den anderen Faktor innerhalb des Radikals zu belassen. Wenn die Zahl eine Quadratzahl ist, können Sie das Wurzelzeichen entfernen, sobald Sie die Quadratwurzel geschrieben haben. Zum Beispiel: √98 kann zu 7√2 . vereinfacht werden.
Tipps
- Eine Möglichkeit, Quadrate zu finden, um Ihre quadrierten Zahlen zu teilen, besteht darin, Quadrate in Ihrer Liste nachzuschlagen, beginnend mit der kleinsten Zahl nach Ihrer quadrierten Zahl. Beispiel: Wenn Sie nach der Quadratzahl 27 suchen, beginnen Sie bei 25 und hören Sie bei 9 auf, weil Sie den größten Teiler gefunden haben, der eine Quadratzahl ist.
Warnungen
- Verwenden Sie keine Taschenrechner, außer in dem Schritt, in dem Sie versuchen herauszufinden, wie oft das Quadrat in die Quadratwurzel eingeht.
- Vereinfachen ist nicht dasselbe wie das Einsetzen von Werten in eine Gleichung.Nirgendwo im gesamten Prozess darf irgendwo eine Dezimalzahl auftauchen!
"Quadratwurzeln vereinfachen"
Оцените, пожалуйста статью