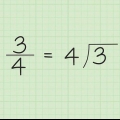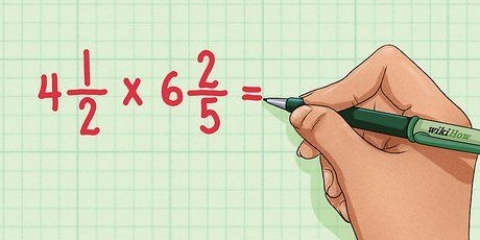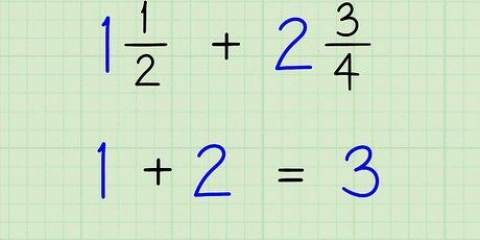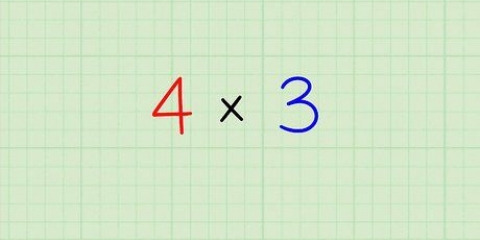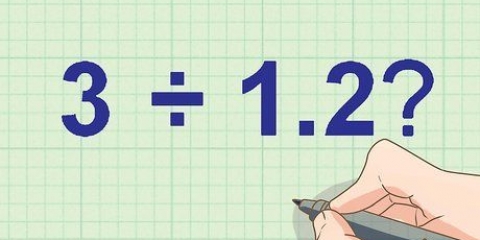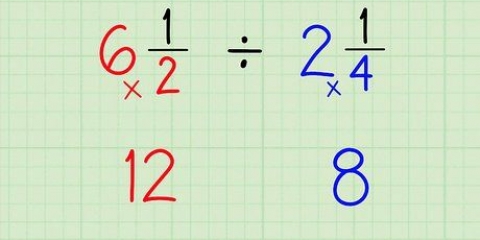wikiHow

Schritte

Die Division ist neben Addition, Subtraktion und Multiplikation eine der vier wichtigsten arithmetischen Operationen. Neben ganzen Zahlen kannst du auch Dezimalzahlen, Brüche oder Exponenten dividieren. Sie können eine lange Division oder, wenn eine der Zahlen eine einzelne Ziffer ist, eine kurze Division durchführen. Beginnen Sie jedoch mit der Beherrschung der langen Division, denn das ist der Schlüssel zur ganzen Operation.

Schritte

Methode 1 von 5: Lange Division

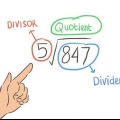
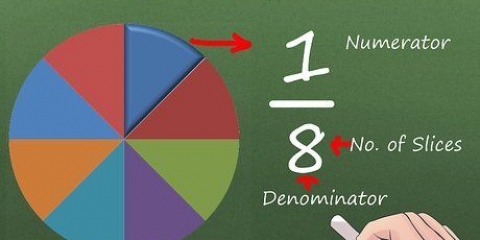
1. Schreiben Sie das Problem mit alanges Divisionszeichen. Das lange Divisionszeichen ( 厂 ) sieht aus wie eine `Endklammer` mit einer Zahl darunter. Platziere den Nenner, die Zahl, die du dividierst, außerhalb des langen Teilungszeichens und den Zähler, die Zahl, die du dividierst, innerhalb des langen Teilungszeichens .

Beispielaufgabe #1 (Anfänger): 65 5. Platziere die 5 außerhalb der Division und die 65 darin. So sollte es aussehen 5厂65, aber mit der 65 unter der horizontalen Linie.
Beispielübung #2 (Fortgeschrittene): 136 3. Platziere die 3 außerhalb der Teilung und die 136 darin. So sollte es aussehen 3厂136, aber mit der 136 unter der horizontalen Linie.

2. Teilen Sie die erste Ziffer des Zählers durch den Nenner. Mit anderen Worten, finden Sie heraus, wie oft der Nenner (die Zahl außerhalb des Divisionszeichens) in die erste Ziffer des Zählers eingeht. Platziere das ganzzahlige Ergebnis über dem Divisionszeichen, direkt über der ersten Ziffer des Nenners.

In Übung 1 (5厂65), 5 ist der Nenner und 6 ist die erste Ziffer des Zählers (65). 5 geht einmal in 6, also setze eine 1 auf das Divisionszeichen über der 6.

In Übung #2 (3厂136), 3 (der Teiler) passt nicht vollständig in 1 (die erste Ziffer des Zählers). Schreiben Sie in diesem Fall eine 0 über das Divisionszeichen, über die 1.

3. Multipliziere die Zahl über dem Divisionszeichen mit dem Nenner. Nimm die Zahl, die du direkt über der Division geschrieben hast, und multipliziere sie mit dem Nenner (die Zahl links von der Division). Schreiben Sie das Ergebnis in eine neue Zeile unter dem Zähler, ausgerichtet an der ersten Ziffer des Zählers.

In Übung 1 (5厂65), multipliziere die Zahl über dem Balken (1) mit dem Nenner (5), so dass 1 x 5 = 5, und platziere die Antwort (5) knapp unter 6 von 65.

In Übung #2 (`3厂136) über dem Divisionszeichen befindet sich eine Null. Wenn Sie diese also mit 3 (dem Nenner) multiplizieren, ist das Ergebnis Null. Schreiben Sie eine Null in eine neue Zeile knapp unter 1 von 136.

4. Subtrahiere das Produkt (Ergebnis der Multiplikation) von der ersten Ziffer des Zählers. Mit anderen Worten, subtrahiere die Zahl, die du gerade in die neue Zeile unter dem Zähler geschrieben hast, von der Zahl im Zähler direkt darüber. Schreiben Sie das Ergebnis in eine neue Zeile, ausgerichtet unter den Zahlen der Subtraktion.

In Übung 1 (5厂65), subtrahiere die 5 (das Produkt in der neuen Zeile) von der 6 darüber (die erste Ziffer des Zählers): 6 - 5 = 1. Platziere das Ergebnis (1) in einer anderen neuen Zeile direkt unter 5.

In Übung #2 (3厂136) subtrahiere die 0 (das Produkt in der neuen Zeile) von der 1 oben rechts (die erste Ziffer im Zähler). Platziere das Ergebnis (1) in einer anderen neuen Zeile direkt unter der 0.

5. Bringen Sie die zweite Ziffer des Zählers herunter. Bringen Sie die zweite Ziffer des Zählers in die neue untere Reihe, direkt rechts neben dem Ergebnis der gerade erhaltenen Subtraktion.

In Übung 1 (5厂65), ziehe die 5 von 65 herunter, so dass sie neben der 1 liegt, die du durch Subtrahieren von 5 von 6 . erhältst. Es sind jetzt 15 in dieser Reihe.

In Übung #2 (3厂136), ziehe die 3 von 136 herunter und platziere sie neben der 1, was dir 13 . ergibt.

6. Wiederholen Sie die lange Division (Aufgabe 1). Verwenden Sie dieses Mal den Zähler (die Zahl links vom Divisionszeichen) und die neue Zahl in der unteren Reihe (das Ergebnis Ihrer ersten Matherunde und die Ziffer, die Sie übertragen haben). Dividiere, multipliziere und subtrahiere deine Zahlen wie zuvor, um das Ergebnis zu erhalten.

Um fortzufahren mit 5厂65, dividiere die neue Zahl (15) durch 5 (den Nenner) und schreibe das Ergebnis (3, weil 15 ÷ 5 = 3) rechts von der 1 über dem Divisionszeichen. Dann multipliziert man diese 3 über dem Divisionszeichen mit 5 (dem Nenner) und schreibt das Ergebnis (15, weil 3 x 5 = 15) unter 15 unter dem Divisionszeichen. Ziehe schließlich 15 von 15 ab und schreibe 0 in eine neue untere Zeile.

Beispielaufgabe Nr. 1 ist jetzt abgeschlossen, da es keine Zahlen mehr im Nenner gibt, die heruntergezählt werden müssen. Die Antwort (13) steht über dem Divisionszeichen.

7. Lange Division wiederholen (Aufgabe #2). Beginnen Sie wie zuvor mit Division, Multiplikation und Subtraktion.

Für 3厂136: Bestimme, wie oft 3 vollständig in 13 geht und schreibe die Antwort (4) rechts von der 0 über dem Divisionszeichen. Dann multipliziere 4 mit 3 und schreibe die Antwort (12) unter 13. Subtrahiere schließlich 12 von 13 und schreibe die Antwort (1) unter 12.

8. Mach noch eine lange Divisionsrunde und du bekommst den Rest (Aufgabe #2). Wenn Sie mit diesem Problem fertig sind, beachten Sie, dass ein Rest übrig bleibt (d. h. eine Zahl, die am Ende Ihrer Berechnung übrig bleibt). Diesen Rest legst du neben deine gesamte Antwort.

Für 3厂136: Setzen Sie den Prozess für die nächste Runde fort. Bringen Sie die 6 von 136 herunter und lassen Sie 16 in der unteren Reihe. Dividiere 16 durch 3 und schreibe das Ergebnis (5) über das Divisionszeichen. Multipliziere 5 mit 3 und schreibe das Ergebnis (15) in eine neue untere Zeile. Subtrahiere 15 von 16 und schreibe das Ergebnis (1) in eine neue untere Zeile.

Da der Zähler keine Ziffern mehr enthält, ist das Problem erledigt und die 1 in der unteren Zeile ist der Rest (die Zahl, die übrig bleibt). Schreiben Sie es über dem Divisionszeichen, möglicherweise mit einem `r.`vorher damit deine endgültige Antwort `45 r.1` wird.

Methode 2 von 5: Kurze Division

1. Verwenden Sie einen Bindestrich, um das Problem aufzuschreiben. Platziere den Nenner, die Zahl, durch die du teilst, außerhalb (und links davon) der Trennlinie. Platzieren Sie den Zähler, die Zahl, die Sie teilen möchten, innerhalb (rechts von und unterhalb) der Teilungslinie.

Zu schnell zu teilen, darf der Nenner nur aus einer Ziffer bestehen.
Abtretung: 518 4. In diesem Fall befindet sich die 4 außerhalb der Trennlinie und die 518 darin.

2. Teilen Sie die erste Ziffer des Zählers durch den Nenner. Mit anderen Worten, bestimmen Sie, wie oft die Zahl außerhalb des Teilers in die erste Ziffer der Zahl innerhalb des Teilers passt. Schreiben Sie die ganze Zahl des Ergebnisses über den Divisionsstrich und schreiben Sie den Rest hochgestellt neben die erste Ziffer des Zählers.

In diesem Problem passt 4 (der Nenner) einmal in 5 (die erste Ziffer des Zählers) mit einem Rest von 1 (5 ÷ 4 = 1 r.1). Platziere den Quotienten 1 über der langen Trennlinie. Setzen Sie eine kleine, hochgestellte 1 neben die 5, um sich daran zu erinnern, dass Sie noch 1 . übrig hatten.

Die 518 unter der Trennlinie sollte nun so aussehen: 518.

3. Teilen Sie den Rest und die zweite Ziffer des Zählers durch den Nenner. Behandeln Sie die hochgestellte Zahl, die den Rest angibt, als vollwertige Ziffer und kombinieren Sie sie mit der Ziffer des Zählers unmittelbar rechts davon. Bestimmen Sie, wie oft der Nenner vollständig in diese neue 2-stellige Zahl passt, und schreiben Sie die ganze Zahl und den Rest wie zuvor.

In der Aufgabe ist die Zahl, die aus dem Rest und der zweiten Zahl des Zählers gebildet wird, 11. der Nenner (4), geht zweimal in 11 und lässt einen Rest von 3 übrig (11 ÷ 4 = 2 r.3) Überreste. Schreiben Sie die 2 über der Trennlinie (was Ihnen 12 ergibt) und die 3 als hochgestellte Zahl neben der 1 in 518.

Der ursprüngliche Zähler, 518, sollte jetzt so aussehen: 518.

4. Wiederholen Sie dies, bis Sie den gesamten Zähler durchlaufen haben. Bestimmen Sie weiterhin, wie oft der Nenner in die Zahl eingeht, die aus der nächsten Ziffer des Zählers und dem Rest direkt links davon hochgestellt wird. Wenn du alle Ziffern des Zählers durchgegangen bist, hast du deine Antwort.

In der Aufgabe ist 38 die nächste (und letzte) Zahl des Zählers – der Rest 3 aus dem vorherigen Schritt und die Zahl 8 ist der letzte Term des Zählers. Der Nenner (4) geht neunmal in 38 mit einem Rest von 2 (38 ÷ 4 = 9 r.2), weil 4 x 9 = 36, das sind zwei weniger als 38. Schreiben Sie diesen letzten Rest (2) über die Trennlinie, um Ihre Antwort zu vervollständigen.

Ihre letzte Antwort über dem Teiler ist also 129 r.2..

Methode 3 von 5: Brüche teilen

1. Schreibe die Divisionssumme so, dass die beiden Brüche nebeneinander liegen. Zu Brüche dividieren, schreibe den ersten Bruch gefolgt vom Divisionssymbol (÷) und dann den zweiten Bruch.

Die Aussage könnte beispielsweise so lauten: 3/4 5/8. Verwenden Sie der Einfachheit halber horizontale statt diagonale Linien, um den Zähler (obere Zahl) und den Nenner (untere Zahl) eines beliebigen Bruchs zu trennen.

2. Vertausche Zähler und Nenner des zweiten Bruchs. Der zweite Bruch wird zu seiner eigenen Umkehrung.

In dieser Beispielaufgabe werden wir 5/8 umkehren, sodass die 8 oben und die 5 unten ist.

3. Ändere den Divisionsbalken in ein Multiplikationszeichen. Um Brüche zu teilen, multipliziere den ersten Bruch mit dem Kehrwert des zweiten.

Zum Beispiel: 3/4 x 8/5.

4. Multipliziere die Zähler der Brüche. Gehen Sie wie bei der Multiplikation zweier Brüche vor.

In diesem Fall sind die Zähler 3 und 8, und 3 x 8 = 24.

5. Multiplizieren Sie die Nenner der Brüche auf die gleiche Weise. Auch dies ist genau das, was Sie tun würden, um zwei Brüche zu multiplizieren.

Die Nenner sind 4 und 5 im Problem, und 4 x 5 = 20.

6. Stelle das Produkt der Zähler über das Produkt der Nenner. Nachdem Sie nun die Zähler und Nenner beider Brüche multipliziert haben, können Sie das Produkt der beiden Brüche bilden.

Im Auftrag: 3/4 x 8/5 = 24/20.

7. Vereinfache den Bruch, falls nötig. Um den Bruch zu vereinfachen, den größten gemeinsamen Teiler bestimmen, oder die größte Zahl, die vollständig in beide Zahlen passt, und dann Zähler und Nenner durch diese Zahl dividieren.

Im Fall von 24/20 ist 4 die größte Zahl, die gleichmäßig in 24 und 20 geht. Sie können dies bestätigen, indem Sie alle Teiler beider Zahlen ausschreiben und die größte Zahl wählen, die ein Teiler von beiden ist:

24: 1, 2, 3, 4, 6, 8, 12, 24

20: 1, 2, 4, 5, 10, 20

Da 4 der größte gemeinsame Teiler von 24 und 20 ist, dividiere beide Zahlen durch 4, um den Bruch zu vereinfachen.

24/4 = 6

20/4 = 5

24/20 = 6/5. So: 3/4 5/8 = 6/5

8. Schreibe den Bruch ggf. in eine gemischte Zahl um. Dividiere dazu den Zähler durch den Nenner und schreibe das Ergebnis als ganze Zahl. Der Rest (die verbleibende Zahl) ist der Zähler des neuen Bruchs. Der Nenner des Bruches bleibt gleich.

In der Aufgabe geht 5 einmal in 6 mit einem Rest von 1. Die neue ganze Zahl ist also 1, der neue Zähler ist 1, und der Nenner bleibt 5.

Das Ergebnis: 6/5 = 1 1/5.

Methode 4 von 5: Exponenten dividieren

1. Stellen Sie sicher, dass die Exponenten die gleiche Basis haben. Sie können Exponenten dividieren wenn sie die gleiche basis haben. Wenn sie nicht die gleiche Basis haben, müssen Sie sie manipulieren, bis sie es tun, wenn Sie können.

Wenn Sie gerade damit beginnen, lösen Sie zuerst eine Aufgabe, bei der beide Exponenten bereits die gleiche Basis haben. Zum Beispiel: 3 3.

2. Subtrahiere die Exponenten voneinander. Subtrahiere einfach den zweiten Exponenten vom ersten. Mach dir vorerst keine Sorgen um die Basis.

Im Auftrag: 8 - 5 = 3.

3. Platzieren Sie den neuen Exponenten über der ursprünglichen Basis. Schreiben Sie einfach den neuen Exponenten über die ursprüngliche Basis. Das ist alles!

Daher: 3 3 = 3.

Methode 5 von 5: Dezimalzahlen dividieren

1. Schreiben Sie das Problem mit einem Bindestrich. Platzieren Sie den Nenner, die Zahl, durch die Sie dividieren, außerhalb (und links davon) des langen Teilungsstrichs und den Zähler, die Zahl, durch die Sie dividierten, innerhalb des langen Teilungsstrichs. Zu Dezimalzahlen dividieren, Konvertieren Sie Dezimalzahlen zuerst in ganze Zahlen.

Im Beispiel 65,5 0,5 wird 0,5 außerhalb der Trennlinie und 65,5 innerhalb der Trennlinie platziert.

2. Verschieben Sie die Dezimalpunkte gleichmäßig, um zwei ganze Zahlen zu erstellen. Schieben Sie einfach die Dezimalpunkte nach rechts, bis sie am Ende jeder Zahl stehen. Stellen Sie sicher, dass Sie für jede Zahl die gleiche Anzahl von Stellen verschieben - wenn Sie den Dezimalpunkt im Nenner um zwei Stellen verschieben müssen, machen Sie dasselbe für den Zähler.

In der Aufgabe müssen Sie nur den Dezimalpunkt sowohl für den Nenner als auch für den Zähler um eine Stelle verschieben. Also: 0,5 wird zu 5 und aus 65,5 wird 655.

Wenn die Zahlen in der Aufgabe jedoch 0,5 und 65,55 wären, würden Sie den Dezimalpunkt um zwei Stellen in 65,55 verschieben, was 6555 . ergibt. Daher sollten Sie auch den Dezimalpunkt um 0,5 um zwei Stellen verschieben. Fügen Sie dazu am Ende eine Null hinzu und machen Sie es 50.

3. Platziere den Dezimalpunkt direkt über der Teilungslinie. Setzen Sie eine Dezimalstelle auf das lange Divisionszeichen direkt über der Dezimalstelle im Zähler.

In der Anweisung kommt die Dezimalstelle in 655 nach den letzten 5 (als 655.0). Schreiben Sie also den Dezimalpunkt über der Teilungslinie direkt über dem Dezimalpunkt in 655.

4. Lösen Sie das Problem, indem Sie eine lange Division durchführen. Um 655 durch 5 zu teilen, gehen Sie wie folgt vor:

Teilen Sie das Hundertstel (6) durch 5. Sie erhalten dann 1 mit Rest 1. Platziere 1 an der hundertsten Stelle oben auf der langen Trennlinie und subtrahiere 5 von 6 unter der Zahl sechs.

Der Rest, 1 bleibt. Bringen Sie die ersten fünf in 655 herunter und Sie erhalten die Zahl 15. Teilen Sie 15 durch 5 und Sie erhalten 3. Platziere die drei über dem langen Divisionszeichen neben der 1.

Bringen Sie die letzten 5 . herunter. Teilen Sie 5 durch 5 und Sie erhalten 1 – platzieren Sie die 1 über dem langen Teilungszeichen. Es gibt keinen Rest, da 5 einmal in 5 geht.

Die Antwort ist die Zahl über dem langen Divisionszeichen (131), also 655 5 = 131. Wenn Sie einen Taschenrechner herausziehen, sehen Sie, dass dies auch die Antwort auf die ursprüngliche Teilung ist: 65,5 0,5.