Kostenlose Schritt für Schritt Anweisungen 
Faktorisierung in Primfaktoren: 24 = 2 x 2 x 2 x 3 und 84 = 2 x 2 x 3 x 7 Bestimmen Sie gemeinsame Primfaktoren: 24 = 2 x 2 x 2 x 3 und 84 = 2 x 2 x 3 x 7 Multiplikation gemeinsamer Primfaktoren: 2 x 2 x 3 = 12
Den größten gemeinsamen teiler finden
Den größten gemeinsamen Teiler (GGD) einer Reihe von Zahlen zu bestimmen ist einfach, aber Sie müssen mehrere Schritte befolgen, um dorthin zu gelangen. Um den größten gemeinsamen Teiler zweier Zahlen zu finden, müssen Sie beide Zahlen mit Ihrem Wissen über Multiplikationstabellen faktorisieren und dann die größte Zahl in beiden Sätzen von Faktoren finden.
Schritte
Methode 1 von 2: Gemeinsame Nenner vergleichen
1. Bestimmen Sie die Faktoren der Zahl. Sie brauchen keine Primfaktoren, um den größten gemeinsamen Teiler zu finden. Beginnen Sie damit, alle Faktoren der Zahlen zu finden, die Sie vergleichen.
2. Vergleichen Sie die Sätze von Faktoren, bis Sie die größte Zahl in beiden Sätzen finden.
Methode 2 von 2: Primzahlen verwenden
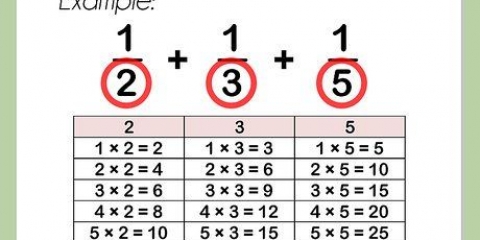
1. Faktoriere jede Zahl vollständig in Primzahlen. Eine Primzahl ist eine Zahl größer als 1, die nur durch 1 und sich selbst teilbar ist. Beispiele für Primzahlen sind 5, 17, 97 und 331, um nur einige zu nennen. Zum Beispiel:
- 42 = 2 x 3 x 7
- 35 = 5 x 7
- Die Faktorisierung einer Primzahl in Primfaktoren ist einfach selbst. 5 = 5, 23 = 23 usw.
2. Bestimmen Sie die gemeinsamen Primfaktoren. Wählen Sie aus allen Primzahlen zwischen den Sätzen, die gleich sind. Es kann mehrere gemeinsame Primteiler geben.
3. Berechnung. Wenn es nur einen gemeinsamen Primfaktor gibt, ist das Ihr gemeinsamer Nenner. Wenn es mehrere gemeinsame Primfaktoren gibt, multiplizieren Sie alle gemeinsamen Primfaktoren miteinander, um den größten gemeinsamen Teiler zu erhalten.
4. Um diese Methode zu demonstrieren, untersuchen wir das folgende Beispiel. Finden Sie den größten gemeinsamen Teiler von 24 und 84.
Tipps
- Eine Primzahl ist eine Zahl, die nur durch 1 und sich selbst geteilt werden kann.
- Wussten Sie, dass der Mathematiker Euklid aus dem 3. Jahrhundert v. Chr. einen Algorithmus entwickelt hat, um den größten gemeinsamen Teiler von zwei natürlichen Zahlen oder zwei Polynomen zu finden??
"Den größten gemeinsamen teiler finden"
Оцените, пожалуйста статью
