Beachten Sie, dass Sie, wenn es derzeit kein gemeinsames Vielfaches gibt, fortfahren müssen, bis Sie ein Vielfaches finden, das für beide Nenner gültig ist. Beispiel: 2 *15=30; 3 *10=30; 5 *6=30 Das kgv=30 
Beispiel: 15 *(1/2); 10 * (1/3); 6 *(1/5) Neue Summe: 15/30 + 10/30 + 6/30 
Beispiel: 15/30 + 10/30 + 6/30=31/30=1 1/30 

In unserem Beispiel teilen sich 8 und 12 den Nenner 1, 2 und 4. Der größte gemeinsame Teiler ist 4. 
Beispiel: 8 *12=96 
Beispiel: 96 / 4=24 
Beispiel: 24 / 8=3; 24 / 12=2 3 * (3/8) = 9/24; 2 * (5/12) = 10/24 9/24 + 10/24 
Beispiel: 9/24 + 10/24=19/24 

Beispiel: Es gibt zwei 2-und in 4; Null 2-und in 5; zwei 2-und in 12 Es gibt null 3-und in 4 und 5; ein 3 in 12 Es gibt null 5-und in 4 und 12; ein 5 in 5 
Beispiel: Die größte Zahl für 2 ist zwei; die größte Zahl für 3 ist ein; die größte Zahl für 5 ist ein. 
Beispiel: 2, 2, 3, 5 
Beispiel: 2 *2 *3 *5=60 kgf=60 
Beispiel: 60/4=15; 60/5=12; 60/12=5 15 * (1/4) = 15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60 15/60 + 12/60 + 5/60 
Beispiel: 15/60 + 12/60 + 5/60=32/60=8/15 

Beachten Sie, dass Sie keine Vielfachen von auflisten müssen 1 denn jede Zahl ist ein Vielfaches von 1. Beispiel: 4 *1=4; 4 * 2 = 8; 4 *3=12; 4 * 4 = 16; etc. 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 *4=12; etc. Das kgv=12 
Beispiel: 12 *(8/1)=96/12; 3 * (9/4) = 27/12; 4 * (2/3) = 8/12 96/12 + 27/12 + 8/12 
Beispiel: 96/12 + 27/12 + 8/12=131/12=10 11/12
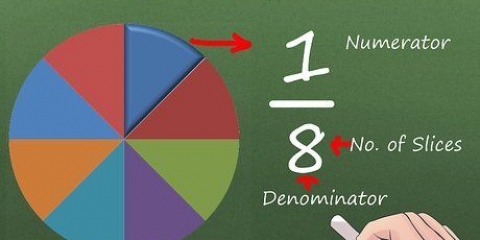
Finde das kleinste gemeinsame vielfache von zwei nennern
Brüche mit unterschiedlichen Nennern addieren oder subtrahieren. es ist notwendig, zuerst das kleinste gemeinsame Vielfache dieser beiden Zahlen zu finden. Dies ist das kleinste Vielfache eines Nenners in einer Gleichung. Hier sind einige verschiedene Methoden, mit denen Sie den lcm finden und zum Lösen von Bruchproblemen verwenden können.
Schritte
Methode 1 von 4: Vielfache auflisten

1. Listen Sie die Vielfachen jedes Nenners auf. Jede Liste sollte aus dem Nenner des Bruchs multipliziert mit 1, 2, 3, 4 usw. bestehen.
- Beispiel: 1/2 + 1/3 + 1/5
- Vielfaches von 2: 2 *1=2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 *6=12; 2 * 7 = 14; etc.
- Vielfaches von 3: 3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 *4=12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; etc.
- Vielfaches von 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; etc.

2. Finde das kleinste gemeinsame Vielfache. Durchsuchen Sie jede Liste und markieren Sie ein gemeinsames Vielfaches beider Nenner. Bestimmen Sie nach der Bestimmung der gemeinsamen Vielfachen, welches das kleinste ist.

3. Schreiben Sie das ursprüngliche Problem um. Um jeden Bruch in diese Summe so zu schreiben, dass er denselben Wert wie das ursprüngliche Problem hat, müssen Zähler und Nenner des Bruchs mit dem entsprechenden Wert multipliziert werden, der dem gefundenen gemeinsamen Vielfachen entspricht.

4. Lösen. Nachdem Sie die LCF gefunden haben und die Brüche modifiziert wurden, sollten Sie dieses Problem problemlos lösen können.
Methode 2 von 4: Den größten gemeinsamen Teiler verwenden

1. Finden Sie den größten gemeinsamen Teiler jedes Nenners. Finden Sie heraus, ob es für beide Nenner einen größten gemeinsamen Teiler gibt, indem Sie herausfinden, welche Zahlen durch die Nenner teilbar sind.
- Beispiel: 3/8 + 5/12
- Faktoren von 8: 1, 2, 4, 8
- Faktoren von 12: 1, 2, 3, 4, 6, 12

2. Identifizieren Sie den größten gemeinsamen Teiler zwischen beiden Nennern. Kreisen Sie alle GCDs ein, nachdem Sie die Faktoren jedes Nenners gefunden haben. Der größte der GCDs ist der größte gemeinsame Nenner, mit dem Sie das Problem weiter lösen können.

3. Multipliziere die Nenner miteinander. Gehen Sie zum nächsten Schritt, indem Sie die beiden Nenner miteinander multiplizieren.

4. Von der gcd teilen. Nachdem Sie das Produkt beider Nenner gefunden haben, dividieren Sie dieses durch die zuvor gefundene gcd. Das Ergebnis dieser Division ist dein kleinstes gemeinsames Vielfaches.

5. Schreiben Sie das ursprüngliche Problem um. Schreiben Sie die Zähler um, indem Sie sie mit derselben Zahl multiplizieren, die erforderlich ist, um die entsprechenden Nenner gleich dem lcg . zu machen. Ermitteln Sie den Faktor für jeden Bruch, indem Sie lcm durch den ursprünglichen Nenner dividieren.

6. Das Problem lösen. Mit den gefundenen kgv sollte es nun problemlos möglich sein, zu addieren und zu subtrahieren.
Methode 3 von 4: Brüche in Primfaktoren faktorisieren

1. Teile die Nenner in Primzahlen. Teile jeden Nenner in eine Reihe von Primzahlen. Denken Sie daran, dass Primzahlen diejenigen Zahlen sind, die durch keine andere Zahl außer 1 und sich selbst geteilt werden können.
- Beispiel: 1/4 + 1/5 + 1/12
- Die Primfaktoren von 4: 2 * 2
- Die Primfaktoren von 5: 5
- Die Primfaktoren von 12: 2 * 2 * 3

2. Zählen Sie, wie oft jede Primzahl in der Menge der Primfaktoren vorkommt. Turf die Häufigkeit, mit der jede Primzahl in den Primfaktoren jedes Nenners vorkommt.

3. Nimm die größte Zahl für eine beliebige Primzahl. Notieren Sie, wie oft Sie jede Primzahl verwendet haben.

4. Schreiben Sie dies als Beispiel unten.

5. Multipliziere alle Primzahlen wie folgt. Multiplizieren Sie die Primzahlen aus der vorherigen Reihe. Das Produkt dieser Zahlen ist gleich lcm des ursprünglichen Problems.

6. Schreiben Sie das ursprüngliche Problem um. Teilen Sie den LCF durch den ursprünglichen Nenner. Multiplizieren Sie jeden Zähler mit der gleichen Zahl, die benötigt wird, um den entsprechenden Nenner zum LCF . zu machen.

7. Lösen. Mit dem gefundenen LCF und ähnlichen Nennern ist es einfach geworden, die Brüche wie gewohnt zu addieren und zu subtrahieren.
Methode 4 von 4: Mit ganzen Zahlen und gemischten Zahlen arbeiten

1. Wandeln Sie jede ganze Zahl und gemischte Zahl in einen unechten Bruch um. Wandeln Sie gemischte Zahlen in unechte Brüche um, indem Sie die ganze Zahl vor dem Bruch mit dem Nenner multiplizieren und den Zähler zum Produkt addieren. Wandeln Sie eine ganze Zahl in einen unechten Bruch um, indem Sie sie als Zähler in einem Bruch mit dem Nenner `1` platzieren.
- Beispiel: 8 + 2 1/4 + 2/3
- 8=8/1
- 2 1/4; 2 * 4 + 1 = 8 + 1 = 9; 9/4
- Umgeschriebene Aufgabe: 8/1 + 9/4 + 2/3

2. Finden Sie das kleinste gemeinsame Vielfache der Nenner. Wenden Sie eine der oben beschriebenen Methoden an, um die LCF eines gemeinsamen Bruchs zu ermitteln. Beachten Sie, dass wir in diesem Beispiel die Methode `Vielfache auflisten` verwenden, eine Liste von Vielfachen für jeden Nenner erstellen und daraus den lcm ableiten.

3. Schreiben Sie das ursprüngliche Problem um. Anstatt nur den Nenner zu multiplizieren, muss auch der Zähler mit der Zahl multipliziert werden, die benötigt wird, um den Nenner zu einem lcg . zu machen.

4. Das Problem lösen. Nach dem Anpassen des Bruchs und dem Finden des lcm im Nenner sollte es einfach sein, die Brüche problemlos zu addieren und zu subtrahieren.
Notwendigkeiten
- Bleistift
- Papier
- Rechner (optional)
"Finde das kleinste gemeinsame vielfache von zwei nennern"
Оцените, пожалуйста статью