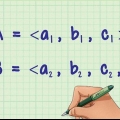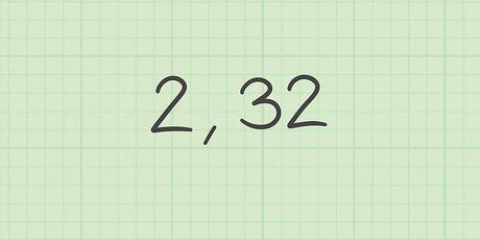Den Winkel zwischen zwei Vektoren finden

Schritte
Tipps

Mathematiker und Physiker müssen oft den Winkel zwischen zwei gegebenen Vektoren finden. Während es einfach ist, den Winkel zwischen zwei Vektoren in derselben Ebene grafisch zu bestimmen, kann es im Raum oder in drei Dimensionen etwas schwieriger sein. Dieser Artikel erklärt die Methode, um den Winkel zwischen zwei Vektoren in der Ebene oder im Raum zu finden.

Schritte

Methode 1 von 4: Bestimme die Vektoren

Den Winkel zwischen zwei Vektoren ermitteln

1. Bestimmen Sie die Vektoren, die Sie benötigen, um den Winkel zu finden. Nimm die beiden Vektoren ZU und OQ die sich im Punkt O schneiden, und berechnen den Winkel MOQ. Sie müssen die Vektoren verwenden ZU und OQ verwenden, nicht MO oder QO. Für den Fall, dass MO bekannt ist, multiplizieren Sie es mit -1, um zu erhalten ZU bekommen.

Methode 2 von 4: Finden Sie das Skalarprodukt

Finden Sie das Skalarprodukt (oder Skalarprodukt) der beiden Vektoren. Wenn Sie nicht wissen, wie man das Skalarprodukt zweier Vektoren berechnet, lesen Sie weiter:

1. Bestimmen Sie die Komponenten des Vektors in jeder Richtung. Wenn die Vektoren in einer Tabelle aufgelistet sind, stellt die erste Zeile normalerweise die x-Achse dar, die zweite Zeile die y-Achse und die dritte die z-Achse. Schreibt man den Vektor in der Form xich + jaJ + zk, dann setze die Koeffizienten von ich, du, und k die Größe der Komponenten entlang der x-, y- und z-Achsen (ich, du, und k sind die Vektoren entlang der x-, y- und z-Achse).

2. Multiplizieren Sie die Komponenten beider Vektoren entlang der x-Achse. Dann multiplizieren Sie die Komponenten beider Vektoren entlang der y-Achse und machen Sie dasselbe für die Komponenten entlang der z-Achse.

3. Füge die drei Produkte zusammen. Dies ist das Skalarprodukt beider Vektoren. Das Skalarprodukt, oder "internes Produkt", von zwei Vektoren ist eine sehr nützliche Zahl in Geometrie und Physik. Im Moment verwenden wir dieses Produkt nur als Werkzeug, um den Winkel zwischen zwei Vektoren zu berechnen. In einem zweidimensionalen Vektor ist die Komponente entlang der z-Achse null, daher kann das Skalarprodukt gefunden werden, indem nur die Komponenten entlang der x- und y-Achse betrachtet werden.

Methode 3 von 4: Berechnen Sie die Größe

1. Berechnen Sie die Größe der beiden Vektoren. Berechnen Sie die Größe der beiden Vektoren mit der Formel a=b+c+d, wodurch ein der Betrag des Vektors ist und b, c, und D die Größe der Komponenten in den drei verschiedenen Richtungen. In der flachen Ebene D gleich Null sein.

Methode 4 von 4: = Finden Sie den Winkel

1. Verwenden Sie die oben berechneten Werte in dieser Formel: cosθ = a.b / |a||b|

2. Leiten Sie daraus den inversen Kosinus ab.

3. Beendet.

Tipps

Sie können diese Methode verwenden, um den Winkel in 3D- oder x-y-z-Graphen zu berechnen, indem Sie die Seiten als Vektoren betrachten und den Vektor als freie Vektoren behandeln.