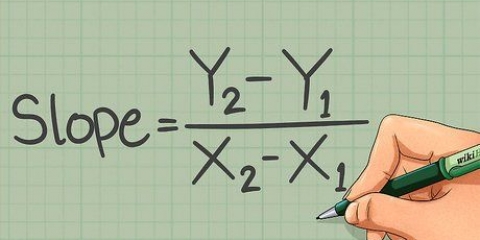Den Abstand zwischen zwei Punkten berechnen: 6 Schritte (mit Bildern)

Schritte
Tipps

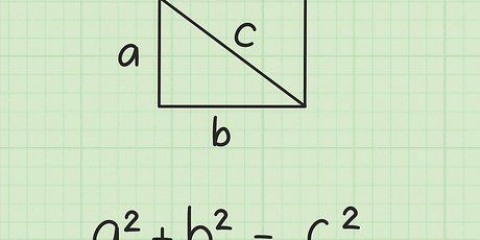
Stellen Sie sich den Abstand zwischen zwei beliebigen Punkten als Linie vor. Die Länge dieser Linie kann mit der Distanzformel ermittelt werden: $\sqrt{(} (x_{2} - x_{1})^{2} + ({ja}_{2} - {ja}_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Schritte

Finden Sie den Abstand zwischen zwei Punkten Schritt 2

1. Nehmen Sie die Koordinaten von zwei Punkten, zwischen denen Sie den Abstand finden möchten. Rufen Sie einen Punkt 1 (x1,y1) und den anderen Punkt 2 (x2,y2) auf. Es spielt keine Rolle, von welchem Punkt aus Sie beginnen, solange Sie die Etiketten (1 und 2) konsequent während des gesamten Problems anbringen.

x1 ist die horizontale Koordinate (entlang der x-Achse) von Punkt 1 und x2 ist die horizontale Koordinate von Punkt 2. y1 ist die vertikale Koordinate (entlang der y-Achse) von Punkt 1 und y2 ist die vertikale Koordinate von Punkt 2.
Nein, zum Beispiel die Punkte (3.2) und (7.8). Wenn (3.2) gleich (x1,y1) ist, dann ist (7.8) gleich (x2,y2).

Finden Sie den Abstand zwischen zwei Punkten Schritt 1

2. Verwenden Sie die Abstandsformel. Diese Formel bestimmt die Länge einer Geraden zwischen zwei Punkten: Punkt 1 und Punkt 2. Der lineare Abstand ist die Quadratwurzel des Quadrats des horizontalen Abstands plus dem Quadrat des vertikalen Abstands zwischen zwei Punkten. Einfach ausgedrückt ist es die Quadratwurzel von:

(x 2 - x_{1})^{2} + ({ja}_{2} - {ja}_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Finden Sie den Abstand zwischen zwei Punkten Schritt 3

3. Bestimmen Sie den horizontalen und vertikalen Abstand zwischen den Punkten. Berechnen Sie zuerst y2 - y1, um den vertikalen Abstand zu finden. Berechnen Sie dann x2 - x1, um den horizontalen Abstand zu finden. Machen Sie sich keine Sorgen, wenn die Subtraktion negative Zahlen ergibt. Der nächste Schritt besteht darin, diese Werte zu quadrieren (was immer eine positive ganze Zahl ergibt).

Bestimmen Sie den Abstand entlang der y-Achse. Für die Beispielpunkte (3.2) und (7.8), wobei Punkt 1 (3.2) und Punkt 2 (7.8) ist, wird dies zu: (y2 - y1) = 8 - 2 = 6. Dies bedeutet, dass der Abstand auf der y-Achse zwischen diesen beiden Punkten sechs Längeneinheiten beträgt.

Bestimmen Sie den Abstand entlang der x-Achse. Für die gleichen Abtastpunkte (3.2) und (7.8): (x2 - x1) = 7 - 3 = 4. Dies bedeutet, dass es vier Längeneinheiten gibt, die die beiden Punkte auf der x-Achse trennen.

Finden Sie den Abstand zwischen zwei Punkten Schritt 4

4. Beide Werte quadrieren. Dies bedeutet, dass Sie den x-Achsen-Abstand quadrieren (x2 - x1) und den y-Achsen-Abstand quadrieren (y2 - y1).

62 = 36

$6^{2}=36$

42 = 16

$4^{2}=16$

Finden Sie den Abstand zwischen zwei Punkten Schritt 5

5. Füge die Quadrate zusammen. Dadurch erhalten Sie das Quadrat der diagonalen, linearen Entfernung zwischen Ihren beiden Punkten. Im Beispiel der Punkte (3.2) und (7.8) ist das Quadrat von (7 - 3) 16 und das Quadrat von (8 - 2) ist 36. 36 + 16 = 52.

Finden Sie den Abstand zwischen zwei Punkten Schritt 6

6. Ziehe die Quadratwurzel der Gleichung. Dies ist der letzte Schritt in der Gleichung. Die lineare Distanz zwischen den beiden Punkten ist die Quadratwurzel der Summe der Quadrate der Distanz auf der x-Achse und der Distanz auf der y-Achse.

Um mit dem Beispiel fortzufahren, ist der Abstand zwischen (3.2) und (7.8) die Quadratwurzel von 52 oder ungefähr 7.21.

Tipps

Es spielt keine Rolle, ob Sie nach der Subtraktion von y2 - y1 oder x2 - x1 eine negative Zahl erhalten. Da die Differenz quadriert wird, erhalten Sie in Ihrer Antwort immer eine positive Distanz.