Beachten Sie jedoch, dass Sie, wenn sich die in Ihrem Durchschnittsgeschwindigkeitswert verwendeten Zeiteinheiten von denen in Ihrem Zeitwert unterscheiden, die eine oder andere entsprechend umrechnen müssen. Wenn beispielsweise eine Durchschnittsgeschwindigkeit in km/h gemessen wird und die Zeit in Minuten angegeben wird, müssen Sie die Zeit durch 60 teilen, um sie in Stunden umzurechnen. Lassen Sie uns unser Beispielproblem lösen. 120 km/h × 0,5 h = 60 km. Beachten Sie, dass die Zeiteinheiten (Stunden) abfallen gegen die Einheiten im Nenner der Durchschnittsgeschwindigkeit (Stunden), wobei nur die Entfernungseinheiten (km) übrig bleiben. 
Angenommen, wir wissen, dass ein Auto in 50 Minuten 60 km zurückgelegt hat, aber wir haben keinen Wert für die Durchschnittsgeschwindigkeit während der Fahrt. In diesem Fall können wir die Variable s . verwendenJuwel isoliere in der Basisgleichung für den Abstand, und wir erhalten sJuwel = d/t zu bekommen. Dann berechnen wir 60 km/50 Minuten = 1,2 km/min. Beachten Sie, dass unsere Antwort für Geschwindigkeit in unserem Beispiel eine ungewöhnliche Einheit (km/Minute) hat. Um Ihre Antwort in der üblicheren Form von km/h zu erhalten, multiplizieren Sie sie mit 60 Minuten/h und erhalten Sie `72 km/h bekommen. 
Beispiel: In der obigen Beispielaufgabe kamen wir zu dem Schluss, dass wir für eine Fahrt von 60 km in 50 Minuten mit 72 km/h fahren müssten. Dies gilt jedoch nur, wenn wir die gesamte Reise mit einer Geschwindigkeit fahren. Wenn wir zum Beispiel die Hälfte der Strecke mit 80 km/h und die andere Hälfte mit 64 km/h fahren, fahren wir immer noch 60 km in 50 Minuten — 72 km/h = 60 km/50 min = ????? Mathematische Lösungen Die Verwendung von Ableitungen ist oft eine bessere Wahl als die Entfernungsformel, um die Geschwindigkeit eines Objekts in realen Situationen zu bestimmen, da Geschwindigkeitsänderungen wahrscheinlich sind. 

Beachten Sie, dass diese Formel absolute Werte verwendet (das Symbol |). Absolute Werte bedeuten einfach, dass die Begriffe innerhalb der Symbole positiv werden, wenn sie negativ sind. Nehmen wir zum Beispiel an, wir halten auf einem perfekt geraden Straßenabschnitt auf dem Weg. Wenn wir eine kleine Stadt 5 km vor uns und eine Stadt 1 km hinter uns haben, wie weit sind die beiden Städte dann voneinander entfernt?? Wenn wir Stadt 1 als x . nehmen1 = betrachte 5 und Stadt 2 als x2 = -1, dann können wir d, den Abstand zwischen den beiden Städten, wie folgt ermitteln: d = |x2 - x1| = |-1 - 5| = |-6| = 6 km. 
Die Distanzformel im zweidimensionalen Raum verwendet die Satz des Pythagoras, die besagt, dass die Hypotenuse eines rechtwinkligen Dreiecks gleich der Quadratwurzel der anderen beiden Seiten ist. Nehmen wir zum Beispiel an, wir haben zwei Punkte in der x-y-Ebene: (3, -10) und (11, 7), die jeweils den Mittelpunkt eines Kreises und einen Punkt auf dem Kreis darstellen. Um den geraden Abstand zwischen diesen beiden Punkten zu ermitteln, können wir Folgendes lösen: d = √((x2 - x1) + (ja2 - ja1)) d = ((11 - 3) + (7 - -10)) d = √(64 + 289) d = (353) = 18.79 
Beispiel: Nehmen wir an, als Astronaut schwebt er im Weltraum in der Nähe von zwei Asteroiden. Einer ist etwa 8 km vor uns, 2 km rechts und 5 km unter uns, der andere 3 km hinter uns, 3 km links und 4 km über uns. Wenn wir die Positionen dieser Asteroiden mit den Koordinaten (8.2,-5) und (-3,-3.4) darstellen, können wir den Abstand zwischen den beiden wie folgt ermitteln: d = ((-3 - 8) + (-3 - 2) + (4 - -5)) d = ((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Entfernung berechnen
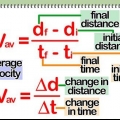
Distanz, oft als Variable bezeichnet D, ist ein Maß für den Raum, den eine Gerade zwischen zwei Punkten einnimmt. Die Distanz kann sich auf den Abstand zwischen zwei stationären Punkten beziehen (z. B. ist die Körpergröße einer Person der Abstand von der Unterseite der Füße bis zur Oberseite des Kopfes) oder kann sich auf den Abstand zwischen der aktuellen Position eines sich bewegenden Objekt und sein Startort. Die meisten Distanzprobleme lassen sich mit den Gleichungen lösen d = sJuwel × t wobei d der Abstand ist, sJuwel die mittlere Geschwindigkeit und t die Zeit oder die Gleichung d = √((x2 - x1) + (ja2 - ja1)), wo (x1, ja1) und (x2, ja2) sind die x- und y-Koordinaten von zwei Punkten.
Schritte
Methode 1 von 2: Distanz mit Durchschnittsgeschwindigkeit und Zeit bestimmen

1. Bestimme die Werte für Durchschnittsgeschwindigkeit und Zeit. Wenn Sie versuchen, die zurückgelegte Entfernung eines sich bewegenden Objekts zu ermitteln, sind zwei Informationen für diese Berechnung unerlässlich: die Geschwindigkeit` (oder Geschwindigkeitsgröße) und dieZeit wohin das Objekt verschoben wurde. Mit diesen Daten ist es möglich, die vom Objekt zurückgelegte Entfernung mit der Formel d = s . zu bestimmenJuwel × t.
- Um die Anwendung der Distanzformel besser zu verstehen, werden wir in diesem Abschnitt ein Beispielproblem lösen. Nehmen wir an, wir fahren mit ca. 120 km/h und wollen wissen, wie weit wir in einer halben Stunde fahren. Von 120 km/h als unser Wert für die Durchschnittsgeschwindigkeit und 0,5 Stunden als Wert für die Zeit werden wir dieses Problem im nächsten Schritt lösen.

2. Multiplizieren Sie die Durchschnittsgeschwindigkeit mit der Zeit. Sobald Sie die durchschnittliche Geschwindigkeit eines sich bewegenden Objekts und die für die Bewegung benötigte Zeit kennen, ist es relativ einfach, die zurückgelegte Entfernung zu ermitteln. Multiplizieren Sie einfach diese beiden Werte zusammen, um Ihre Antwort zu erhalten.

3. Bearbeiten Sie die Gleichung, um nach den anderen Variablen aufzulösen. Die Einfachheit der grundlegenden Distanzgleichung (d = sJuwel × t) macht es ganz einfach, die Gleichung zu verwenden, um neben dem Abstand auch die Werte von Variablen zu finden. Isolieren Sie die Variable, die Sie nach den Grundregeln von . lösen möchten Mathematik, und geben Sie dann die Werte der anderen beiden Variablen ein, um den Wert der dritten zu finden. Mit anderen Worten, um die Durchschnittsgeschwindigkeit Ihres Objekts zu ermitteln, verwenden Sie die Gleichung SJuwel = d/t und um die Zeit zu ermitteln, die ein Objekt zurückgelegt hat, verwenden Sie die Gleichung t = d/sJuwel.

4. Beachten Sie, dass die Variable `sJuwel` in der Abstandsformel bezieht sich auf Durchschnitt Geschwindigkeit. Es ist wichtig zu verstehen, dass die Standardabstandsformel ein vereinfachtes Bild der Bewegung eines Objekts liefert. Die Distanzformel geht davon aus, dass das bewegte Objekt a konstante Geschwindigkeit hat – mit anderen Worten, es geht davon aus, dass sich das sich bewegende Objekt mit einer `gleichförmigen`, unveränderlichen Geschwindigkeit bewegt. Bei abstrakten mathematischen Problemen, wie sie im akademischen Umfeld vorkommen, ist es manchmal noch möglich, die Bewegung eines Objekts mit dieser Annahme zu modellieren. Im wirklichen Leben stellt dieses Modell jedoch oft nicht genau die Bewegung von sich bewegenden Objekten dar, die in Wirklichkeit im Laufe der Zeit beschleunigen, verlangsamen, anhalten und umkehren können.
Methode 2 von 2: Bestimmung des Abstands zwischen zwei Punkten

1. Bestimmung von zwei Punkten in einem flachen Raum. Was ist, wenn Sie, anstatt die Entfernung eines sich bewegenden Objekts zu bestimmen, die Entfernung zwischen zwei stationären Objekten bestimmen müssen?? In solchen Fällen nützt die oben beschriebene geschwindigkeitsbasierte Distanzformel nichts. Glücklicherweise gibt es eine andere Distanzformel, um schnell die kürzeste Distanz zwischen zwei Punkten zu finden. Für diese Formel müssen Sie jedoch die Koordinaten der beiden Punkte kennen. Wenn es sich um einen eindimensionalen Abstand handelt (wie auf einem Zahlenstrahl), sind Ihre Koordinaten zwei Zahlen, x1 und x2. Wenn Sie es mit Entfernungen in zwei Dimensionen zu tun haben, benötigen Sie Werte für zwei Punkte (x,y), (x1,ja1) und (x2,ja2). Schließlich benötigen Sie für drei Dimensionen Werte für (x1,ja1,z1) und (x2,ja2,z2).

2. Bestimmen Sie den Abstand auf einer Linie, indem Sie den Wert der Koordinaten für die beiden Punkte subtrahieren. Die Berechnung des eindimensionalen Abstands zwischen zwei Punkten, wenn Sie den Wert für jeden Punkt kennen, ist einfach. Verwenden Sie einfach die Formel d = |x2 - x1|. In dieser Formel subtrahieren Sie x1 aus von x2 und nimm den absoluten Wert deiner Antwort, um den Abstand zwischen x . zu bestimmen1 und x2 finden. Normalerweise verwendet man die eindimensionale Distanzformel, wenn die beiden Punkte auf einer Zahlengeraden oder -achse liegen.

3. Finden Sie die Entfernung in der Ebene mit dem Satz des Pythagoras. Die Entfernung zwischen zwei Punkten im zweidimensionalen Raum zu finden ist komplizierter als in einer Dimension, aber nicht schwierig. Verwenden Sie einfach die Formel d = √((x2 - x1) + (ja2 - ja1)). In dieser Formel subtrahieren Sie die beiden x-Koordinaten, quadrieren das Ergebnis, subtrahieren die y-Koordinaten, quadrieren das Ergebnis, addieren die beiden Zwischenergebnisse und berechnen die Quadratwurzel, um den Abstand zwischen den beiden zu findenden Punkten zu ermitteln. Diese Formel funktioniert in der zweidimensionalen Ebene – zum Beispiel auf den Standard-x/y-Diagrammen.

4. Bestimmen Sie den dreidimensionalen Abstand, indem Sie die Flächenformel ändern. In drei Dimensionen haben Punkte neben der x- und y-Koordinate auch eine z-Koordinate. Um den Abstand zwischen zwei Punkten im dreidimensionalen Raum zu bestimmen, verwenden Sie d = √((x2 - x1) + (ja2 - ja1) + (z2 - z1)). Dies ist eine modifizierte Form der oben beschriebenen zweidimensionalen Distanzformel, die auch die z-Koordinaten berücksichtigt. Indem Sie die beiden Z-Koordinaten voneinander subtrahieren, quadrieren und den Rest der Formel wie oben beschrieben durchlaufen, werden Sie sicher sein, dass Ihre endgültige Antwort den dreidimensionalen Abstand zwischen den beiden Punkten widerspiegelt.
Оцените, пожалуйста статью