Kostenlose Schritt für Schritt Anweisungen 
Verschiebung = D Die Verschiebung ist die Entfernung, die ein bestimmtes Objekt zurückgelegt hat. Normalerweise wird die Einheit der Verschiebung in Meter angegeben. Zeit = T Geschwindigkeit = v Die vektorielle Geschwindigkeit ist die Geschwindigkeit eines Objekts in eine bestimmte Richtung. Bei der Berechnung der Momentangeschwindigkeit suchen wir nach der Geschwindigkeit eines Objekts zu einem bestimmten Zeitpunkt t (Zeit). Die Geschwindigkeit wird normalerweise in Metern pro Sekunde (m/s) angegeben. Steigung (oder "Neigung") = m Es kann nützlich sein, die Bewegung eines Objekts in einem einfachen x-y-Graphen darzustellen, wobei die Zeit entlang der x-Achse und die Verschiebung entlang der y-Achse aufgetragen sind. Dann ist die Steigung der Geraden an einem bestimmten Punkt die Geschwindigkeit des Objekts. 
Die Geschwindigkeit (v) zu einem bestimmten Zeitpunkt (t) ist gleich der Steigung (Änderungsrate) der obigen Gleichung, wobei die Verschiebung (d) gegen die Zeit (t) aufgetragen ist. 
Eine allgemeine Regel zum Ermitteln der Ableitung: Wenn y = a*x, dann ist die Ableitung a*n*x. Diese Regel wird auf jeden Term des Polynoms angewendet. Die Konstante (die Zahl ohne Variable daneben) verschwindet, weil sie mit 0 multipliziert wird. 
Um die Momentangeschwindigkeit zu berechnen, muss die Steigung eines Graphen für jeden beliebigen Punkt berechnet werden. 
Der Wert, auf den sich die Steigung bewegt, wenn sich H 0 nähert, ist die Grenze. Dies ist gleich der Steigung der Tangente an die Kurve. Die Tangente ist eine Gerade definiert als Parallele zur Parabel über eine unendlich kurze Strecke. Die Steigung der Tangente ist also die Steigung der Parabel/Kurve, wenn H ein infinitesimaler Abstand auf der Geraden wird. Die Tangentengleichung ist die Ableitung der Gleichung der Verschiebungsfunktion, wie in Teil eins. 
Momentangeschwindigkeit berechnen
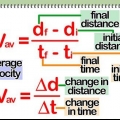
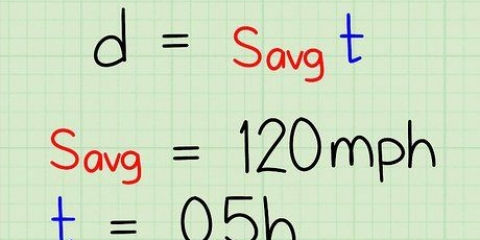Die vektorielle Geschwindigkeit (Geschwindigkeit auf Englisch) ist definiert als die Geschwindigkeit eines Objekts in eine bestimmte Richtung. Für allgemeine Zwecke ist die Ermittlung der Geschwindigkeit eines Objekts so einfach wie die Division der zurückgelegten Entfernung durch die Zeit, die für diese Entfernung benötigt wird. Dies gibt jedoch nur die Durchschnittsgeschwindigkeit entlang einer bestimmten Strecke an. Mit mathematischen Gleichungen und Ableitungen ist es möglich, die Geschwindigkeit des Objekts zu einem bestimmten Zeitpunkt entlang der Bahn zu berechnen. Das nennt man Momentangeschwindigkeit. Der Einfachheit und Lesbarkeit halber beziehen wir uns im Folgenden auf Geschwindigkeit, sowohl wenn wir "normale" Geschwindigkeit als auch vektorielle Geschwindigkeit meinen.
Schritte
Methode 1 von 2: Berechnung der Momentangeschwindigkeit
1. Was ist "Momentangeschwindigkeit". Objekte, die sich bewegen, können dies mit a . tun konstante Geschwindigkeit – das sich während der gesamten Fahrt mit konstanter Geschwindigkeit fortbewegt. Ein Läufer, der über ein Fußballfeld joggt, behält über die gesamte Länge des Feldes ungefähr die gleiche Geschwindigkeit bei. Objekte können sich auch mit a . bewegen unterschiedliche Geschwindigkeit. Ein Auto, das beispielsweise auf einer Straße mit vielen Kurven fährt, hat nicht immer die gleiche Geschwindigkeit – in den Kurven nimmt die Geschwindigkeit ab, um auf den Geraden wieder zu werden.
- Momentane Geschwindigkeit ist ein Maß für die Geschwindigkeit eines Objekts zu einem beliebigen Zeitpunkt. Zum Beispiel ist die Momentangeschwindigkeit einer Rakete genau eine Sekunde nach Zündung des Treibstoffs viel niedriger als ihre Momentangeschwindigkeit 30 Sekunden nach dem Start, wenn die Rakete Zeit hatte, Geschwindigkeit zu gewinnen.
2. Kennen Sie Ihre Variablen. Wenn Sie sich mit Berechnungen der momentanen Geschwindigkeit befassen, werden Sie fast immer irgendwann auf bestimmte Variablen stoßen. Diese Variablen sind:
3. Ein Beispiel. Nehmen wir an, die Verschiebung eines Objekts kann durch eine Gleichung dargestellt werden: Verschiebung(en) = 3t + 4t + 7. Der Graph dieser Funktion ist eine gekrümmte Linie oder Parabel, wobei die x-Achse die Zeit und die y-Achse die Verschiebung darstellt.
4. Um die Momentangeschwindigkeit eines Objekts mit einer Verschiebung gemäß obiger Funktion zu berechnen, benötigen wir die Ableitung dieser Funktion. Die Ableitung einer Funktion ist gleich der Steigung der Funktion an jedem Punkt des Graphen. Um die Ableitung zu finden, differenzieren wir die Funktion nach dieser Formel:
5. Berechnen Sie mit dieser Formel die Ableitung der Funktion. Schreiben wir dies als y = 3x + 4x + 7, dann ist die Ableitung (3*2)*x+(4*1)*x+(7*0)*x
6. Vereinfachen Sie die Gleichung. Die Multiplikation aller Terme in Klammern ergibt 6x+ 4x+ 0x
7. Vereinfachen Sie weiter. Diese Gleichung kann geschrieben werden als 6x + 4. Der "0x" Term wird dann gleich 0, während der "4x" Term wird auf 4 vereinfacht (n = 1.)
8. Machen Sie diese neue Funktion gleich der Steigung m. Wir verwenden diese Ableitungsfunktion, um die Steigung der ursprünglichen Gleichung y = 3x + 4x + 7 für jeden gegebenen Wert von x (Zeit) zu finden. Die ursprüngliche Steigung der Gleichung zu einem bestimmten Zeitpunkt ist die Momentangeschwindigkeit.
9. Ermitteln Sie die momentane Geschwindigkeit des Objekts für t=4 Sekunden. Sie müssen lediglich den Zeitwert in die x-Variable der Ableitung der Gleichung eingeben. Dies ergibt die folgende Gleichung y = 6(4) + 4 . Dies ist vereinfacht auf 28. Die Momentangeschwindigkeit des Objekts für t=4 Sekunden ist 28 m/s.
Methode 2 von 2: Ein Derivat verstehen
1. Zeichne ein gewöhnliches x-y-Koordinatensystem. Um richtig zu verstehen, wie eine Ableitung helfen kann, die Momentangeschwindigkeit eines Objekts zu bestimmen, ist eine grafische Darstellung sehr nützlich. Die y-Achse repräsentiert die Verschiebung des Objekts, während die x-Achse die Zeit repräsentiert.
- Der Graph kann unterhalb der x-Achse fortgesetzt werden. Wenn die Linie, die die Bewegung des Objekts darstellt, unter die x-Achse fällt, bedeutet dies, dass sich das Objekt in die entgegengesetzte Richtung und vor dem Startpunkt bewegt. Normalerweise reicht der Graph nicht über die y-Achse hinaus. Die Geschwindigkeit wird nicht für Objekte gemessen, die sich in der Zeit zurückbewegen!
- Wenn Sie sich nicht sicher sind, wie Sie ein Diagramm zeichnen oder was die x- und y-Achse genau darstellen, erfahren Sie hier, wie es geht kann einen Funktionsgraphen zeichnen.
2. Zeichnen Sie eine gekrümmte Linie, ausgehend vom Punkt auf der Linie x=0, in Richtung der x-Achse. Die Steigung der Geraden ist die Änderungsrate von y geteilt durch die Änderungsrate von x. Wenn also y gleich der Verschiebung und x gleich der Zeit ist, dann ist die Steigung gleich der Geschwindigkeit.
3. Um die Steigung einer Geraden für einen bestimmten Punkt zu ermitteln, verwenden wir einen Trick, bei dem wir den Grenzwert der Gleichung ermitteln. Das Finden des Grenzwertes erfordert zwei Punkte P und Q auf einer gekrümmten Linie und das Finden der Steigung der Linie durch beide Punkte, wenn der Abstand zwischen den beiden Punkten immer kleiner wird.
4. Wähle einen Punkt P auf der Linie. Platziere beispielsweise P auf x=1. Der genaue Standort ist egal. Wählen Sie einen bequemen Wert.
5. Wähle einen zweiten Punkt Q auf der Linie. Q sollte eine kurze Entfernung von P . sein. In unserem Beispiel ist Q an der Stelle mit x=3, während P an der Stelle mit x=1 . ist.
6. Finden Sie die Steigung zwischen P und Q. Die Steigung zwischen P und Q wird dann (die Differenz der y-Werte von P und Q)/(die Differenz der x-Werte von P und Q). Diesen Unterschied der x-Werte von P und Q bezeichnen wir als H. In diesem Fall ist H gleich 3-1=2.
7. Den Wert von H kleiner machen. Mit anderen Worten, bringe Q auf der x-Achse näher an P und berechne dann erneut die Steigung zwischen P und Q. Wiederholen Sie dies und verringern Sie jedes Mal den Abstand zwischen P und Q. Nach ein paar Berechnungen sollte klar sein, dass sich die Steigung einem bestimmten Wert nähert. Solange H>0 wird die Steigung diesen Wert nie erreichen, sondern nur annähern. Wir sagen dann, dass die Steigung die Grenze naht.
8. Verwenden Sie Ableitungen, um die Steigung zu finden, wenn H ein infinitesimales Intervall auf der Geraden darstellt. Die Ableitung einer Gleichung wird gefunden durch "x, ist N*x" auf einen beliebigen Term der ursprünglichen Gleichung anwenden.
Tipps
- Verschiebung ist wie eine Distanz, aber in eine bestimmte Richtung, also ist die Verschiebung ein Vektor und die Geschwindigkeit eine skalare Größe. Die Verschiebung kann negativ sein, während die Entfernung nur positiv sein kann.
- Um die Beschleunigung (die Änderung der Geschwindigkeit im Laufe der Zeit) zu ermitteln, verwenden Sie die Methode in Teil eins, um die Ableitung Ihrer Verschiebungsfunktion zu bestimmen. Dann nimm die Ableitung davon. Daraus ergibt sich dann die Gleichung zur Ermittlung der Beschleunigung zu einem beliebigen Zeitpunkt - Sie müssen lediglich den Zeitwert in diese zweite Ableitung eintragen.
- Die Gleichung, die y (Verschiebung) zu x (Zeit) in Beziehung setzt, kann sehr einfach sein, wie z.B. y= 6x + 3. In diesem Fall ist die Steigung konstant und es ist keine Ableitung der Steigung erforderlich. Es ist gleich 6, gemäß der linearen Gleichung y = mx + b.
"Momentangeschwindigkeit berechnen"
Оцените, пожалуйста статью
