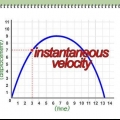
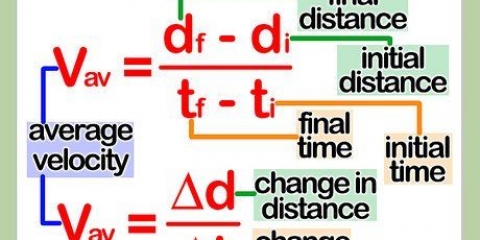
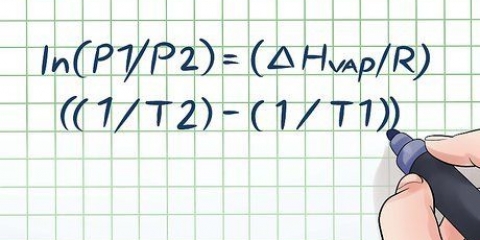Vergessen Sie auch nicht, den Startpunkt mit dem Endpunkt zu verbinden, indem Sie eine gerade Linie verwenden.Dies ist die Verschiebung, die wir berechnen werden. Fährt ein Objekt beispielsweise erst 300 Meter in östlicher Richtung und dann 400 Meter in nördlicher Richtung, entsteht ein rechtwinkliges Dreieck. AB ist die erste Seite und BC ist die zweite Seite des Dreiecks.AC ist die Hypotenuse des Dreiecks und ihr Wert ist die Verschiebung des Objekts. In diesem Beispiel sind die beiden Richtungen "Ost" und "Norden." 
Zum Beispiel x = 300 und y = 400.Ihre Gleichung sieht nun so aus: s = √300² + 400². 
Zum Beispiel: s = √90000 + 160000.s = √250000.s = 500.Sie wissen jetzt, dass die Verschiebung 500 Meter beträgt. 

Die Gleichung sieht so aus: s = 1/2(20 + 23)45. 
Für diese Gleichung spielt es keine große Rolle, wenn Sie die Anfangs- und Endgeschwindigkeit versehentlich vertauschen. Da Sie diese Werte zuerst zusammenzählen, ist es egal. Aber in anderen Gleichungen kann das Vertauschen der Anfangs- und Endgeschwindigkeit die endgültige Antwort oder den Wert der Verschiebung beeinflussen. Ihre Gleichung sieht jetzt so aus: s = 1/2(43)45.Teilen Sie zuerst 43 durch 2, was 21,5 als Antwort ergibt. Multiplizieren Sie 21,5 mit 45, was 967,5 Meter als Antwort ergibt.967,5 ist der Hubraum des Autos, vom Ausgangspunkt aus gesehen. 

Basierend auf dem obigen Beispiel sollte Ihre Gleichung nun so aussehen: s = 25(4) + 1/2(3)4².Es kann sicherlich helfen, wenn Sie die Beschleunigungs- und Zeitwerte in Klammern setzen, um die Zahlen voneinander zu trennen. 
Schauen wir uns die Gleichung genauer an: s = 25(4) + 1/2(3)4². Die Reihenfolge ist: 4² = 16; dann 16 x 3 = 48; dann 25 x 4 = 100; und wenn letzte 48/2 = 24. Die Gleichung sieht nun so aus: s = 100 + 24.Nach der Addition ergibt dies s = 124, die Verschiebung beträgt also 124 Meter. 

Ein Beispiel für eine Aufgabenstellung: Ein Mädchen sitzt auf einem Karussell. Ihr Sitz ist 1 Meter vom Mittelpunkt des Kreises (dem Radius) entfernt. Wenn sich das Mädchen auf einem 1,5 Meter langen Kreisbogen bewegt (lineare Verschiebung), wie groß ist ihre Winkelverschiebung?? Die Gleichung sieht so aus: θ = 1,5/1. 
Nach der Division 1,5/1 bleiben noch 1,5.Die Winkelverschiebung des Mädchens beträgt 1,5 Bogenmaß. Da die Winkelverschiebung angibt, um wie viel ein Objekt von seiner Ausgangsposition gedreht wurde, muss dies im Bogenmaß und nicht als Abstand dargestellt werden. Bogenmaß sind Maßeinheiten für Winkel. 

Verschiebung wird auch als a . bezeichnet "Anzahl der Vektoren" bezeichnet als die Änderung der Position eines Objekts im Vergleich zu der Richtung, in die sich das Objekt bewegt. Angenommen, Sie gehen 5 Meter nach Osten. Wenn du wieder 5 Meter nach Westen gehst, bewegst du dich in die entgegengesetzte Richtung, zurück zu deinem Ausgangspunkt. Obwohl Sie insgesamt 10 Meter gelaufen sind, hat sich Ihre Position nicht geändert und Ihre Verschiebung beträgt daher 0 Meter. 
Stellen Sie sich einen Fußballtrainer vor, der an der Seitenlinie hin und her hüpft.Während er den Spielern Anweisungen gab, ist er mehrmals die Linie entlang gegangen, hin und her. Wenn Sie den Bus ständig im Auge behalten würden, würden Sie die Entfernung sehen, die er zurücklegt. Aber nehmen wir an, der Trainer hält an, um einem Verteidiger etwas zu sagen? Wenn er sich an einem anderen Ort befindet als sein Ausgangspunkt, dann schauen Sie sich die Bewegung des Trainers an (zu einem bestimmten Zeitpunkt). 
Ein kurviger Weg führt Sie schließlich vom Startpunkt zum Endpunkt, aber dies ist nicht der kürzeste Weg. Stellen Sie sich vor, Sie gehen geradeaus und werden von einer Säule oder einem anderen Hindernis angehalten. Du kannst nicht durch die Säule gehen, also gehst du um sie herum. Auch wenn man an der gleichen Stelle landet, als ob man direkt durch die Säule gegangen wäre, musste man dennoch einen längeren Weg dorthin zurücklegen. Obwohl die Verschiebung vorzugsweise in einer geraden Linie erfolgt, ist es möglich, die Verschiebung eines Objekts zu messen, das "Gut" bewegt sich auf einem krummen Pfad. Das nennt man "Winkelverschiebung" und kann berechnet werden, indem die kürzeste Entfernung zwischen Startpunkt und Endpunkt ermittelt wird. 
Angenommen, Sie gehen 5 Meter nach Osten und dann 3 Meter nach Westen. Obwohl Sie technisch gesehen 2 Meter von Ihrem Ausgangspunkt entfernt sind, beträgt die Verschiebung -2, da Sie sich an diesem Punkt in die entgegengesetzte Richtung bewegen.Die Entfernung wird immer positiv sein, weil man die zurückgelegte Strecke nicht kennt "rückgängig gemacht" kann machen. Negative Verschiebung bedeutet nicht, dass die Verschiebung abnimmt. Es ist einfach ein Weg, um anzuzeigen, dass die Bewegung in die entgegengesetzte Richtung erfolgt. 
Dies ist also nur möglich, wenn Sie sich vom Startpunkt aus geradlinig bewegen, und ohne danach die Richtung zu ändern.Angenommen, Sie leben in San Francisco, Kalifornien und finden einen Job in Las Vegas, Nevada. Sie müssen dann nach Las Vegas ziehen, um näher an der Arbeit zu wohnen. Wenn Sie das Flugzeug, einen Direktflug von San Francisco nach Las Vegas, nehmen, haben Sie 670 km zurückgelegt und Ihre Vertreibung beträgt somit 670 km. Wenn Sie jedoch mit dem Auto von San Francisco nach Las Vegas reisen, beträgt Ihre Entfernung möglicherweise immer noch 670 km, aber Sie haben in der Zwischenzeit 906 km zurückgelegt.Da das Fahren in der Regel mit einem Richtungswechsel (Abbiegen, andere Route) verbunden ist, haben Sie eine viel größere Distanz als die kürzeste Distanz zwischen den beiden Städten zurückgelegt.
Verschiebung berechnen
Der Begriff Verschiebung bezieht sich in der Physik eher auf die Veränderung als auf ein Objekt. Bei der Berechnung der Verschiebung messen Sie, wie weit sich ein Objekt bewegt hat, basierend auf den Daten von der Startposition und der Endposition. Die Formel, die Sie verwenden, um die Verschiebung zu bestimmen, hängt von den Variablen ab, die für ein Problem angegeben werden. Führen Sie die folgenden Schritte aus, um zu lernen, wie Sie die Verschiebung eines Objekts berechnen.
Schritte
Teil 1 von 5: Berechnung der resultierenden Verschiebung

1. Verwenden Sie die Formel für die resultierende Verschiebung mit der Längeneinheit, die verwendet wird, um die Start- und Endposition anzugeben. Während sich die Distanz von der Verschiebung unterscheidet, gibt eine Aussage über die resultierende Verschiebung an, um wie viel "Meter" hat ein Objekt abgelegt. Verwenden Sie diese Maßeinheiten, um die Verschiebung zu berechnen, wie weit ein Objekt von seinem ursprünglichen Standort entfernt ist.
- Die Gleichung für die resultierende Verschiebung lautet: s = √x²+y²."S" steht für Verschiebung.X ist die erste Richtung, in die sich das Objekt bewegt, und y ist die zweite Richtung, in die sich das Objekt bewegt. Wenn sich Ihr Objekt nur in 1 Richtung bewegt, dann ist y = 0.
- Ein Objekt kann sich nur in maximal 2 Richtungen bewegen, da eine Bewegung entlang der Nord-Süd-Linie oder der Ost-West-Linie als neutral gilt.

2. Verbinde die Punkte entsprechend der Bewegungsreihenfolge und beschrifte diese Punkte von A-Z.Verwenden Sie ein Lineal, um gerade Linien von Punkt zu Punkt zu zeichnen.

3. Geben Sie die Werte für x² und y² . ein.Da Sie nun wissen, in welche Richtung sich Ihr Objekt bewegt, können Sie damit beginnen, die Werte für die relevanten Variablen einzugeben.

4. Erarbeiten Sie die Gleichung. Berechne zuerst 300² und dann 400², addiere sie und ziehe die Quadratwurzel der Summe ab.
Teil 2 von 5: Den Geschwindigkeitsvektor und die Zeitdauer kennen

1. Verwenden Sie diese Formel, wenn das Problem den Geschwindigkeitsvektor und die Zeitdauer angibt. Es kann vorkommen, dass ein physikalisches Problem kein Wort über die zurückgelegte Strecke sagt, sondern angibt, wie lange und mit welcher Geschwindigkeit ein Objekt gereist ist. Aus der Zeitdauer und der Geschwindigkeit können Sie dann die Verschiebung berechnen.
- In diesem Fall sieht die Gleichung so aus: s = 1/2(u + v)t.u = die Anfangsgeschwindigkeit des Objekts, die Geschwindigkeit, mit der sich das Objekt in eine bestimmte Richtung zu bewegen begann.v = die Endgeschwindigkeit des Objekts oder wie schnell es am Ende ging. t = die Zeit, die das Objekt benötigt hat, um sein Ziel zu erreichen.
- Beispiel: Ein Auto fährt 45 Sekunden.Das Auto bog mit einer Geschwindigkeit von 20 m/s (Anfangsgeschwindigkeit) nach Westen ab und am Ende der Straße beträgt die Geschwindigkeit 23 m/s (Endgeschwindigkeit). Berechnet die Verschiebung basierend auf diesen Daten.

2. Geben Sie die Werte für Geschwindigkeit und Zeit ein. Da Sie nun wissen, wie lange das Auto gefahren ist und wie hoch die Start- und Endgeschwindigkeit war, können Sie die Entfernung vom Startpunkt zum Endpunkt ermitteln.

3. Berechnen Sie die Gleichung, nachdem Sie die Werte eingegeben haben. Denken Sie daran, die Terme in der richtigen Reihenfolge zu berechnen, sonst geht die Verschiebung schief.
Teil 3 von 5: Wenn Geschwindigkeit, Beschleunigung und Zeit vorgegeben sind

1. Eine andere Gleichung ist notwendig, wenn die Beschleunigung für ein Problem zusammen mit der Geschwindigkeit und der Zeit angegeben wird. Bei einer solchen Aufgabe wissen Sie, wie hoch die Anfangsgeschwindigkeit des Objekts war, wie hoch die Beschleunigung ist und wie lange das Objekt auf der Straße war. Sie benötigen die folgende Gleichung.
- Die Gleichung für diese Art von Problem sieht wie folgt aus: s = ut + 1/2at².Der "Sie" stellt immer noch die Anfangsgeschwindigkeit dar; Der "ein" ist die Beschleunigung des Objekts oder auch wie schnell sich die Geschwindigkeit des Objekts ändert. Die Variable"T" kann entweder die Gesamtzeit bedeuten oder einen bestimmten Zeitraum angeben, in dem sich das Objekt beschleunigt hat. Auf jeden Fall wird dies in Zeiteinheiten wie Sekunden, Stunden usw. angegeben.
- Angenommen, ein Auto mit einer Anfangsgeschwindigkeit von 25 m/s erreicht eine Beschleunigung von 3 m/s2 für einen Zeitraum von 4 Sekunden.Wie groß ist der Hubraum des Autos nach 4 Sekunden??

2. Trage die Werte an der richtigen Stelle in die Gleichung ein. Im Gegensatz zur vorherigen Gleichung wird hier nur die Anfangsgeschwindigkeit angezeigt, also stellen Sie sicher, dass Sie die richtigen Werte eingeben.

3. Berechnen Sie die Verschiebung durch Lösen der Gleichung. Eine schnelle Möglichkeit, sich an die Reihenfolge der Operationen in einer Gleichung zu erinnern, ist die Mnemonik "Mr. Dale wartet auf Antwort".Zeigt alle arithmetischen Operationen in der richtigen Reihenfolge an (Übertreibung, Multiplikation, Division, Quadrieren, Addition und Subtraktion).
Teil 4 von 5: Berechnung des Winkelversatzes

1. Bestimmung der Winkelverschiebung, wenn sich ein Objekt entlang einer Kurve bewegt. Dabei wird zwar noch die Verschiebung mit einer Geraden berechnet, aber man benötigt die Differenz zwischen Start- und Endposition entlang einer Kurvenbahn.
- Nehmen Sie als Beispiel ein Mädchen, das auf einem Karussell ist. Während sie sich um die Außenseite des Rades dreht, bewegt sie sich im Kreis. Winkelverschiebung versucht den kürzesten Abstand zwischen Start- und Endposition zu finden, wenn sich ein Objekt nicht gerade bewegt.
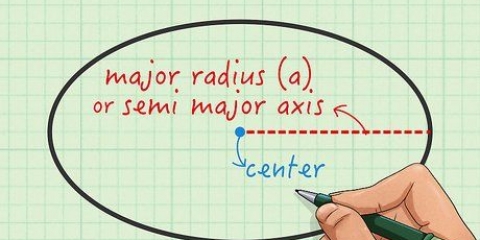
- Die Formel für die Winkelverschiebung lautet: θ = S/r, wodurch "S" steht für die lineare Verschiebung, "R" für den Radius und "θ" die Winkelverschiebung ist.Lineare Verschiebung ist die Entfernung, die ein Objekt entlang eines Kreises zurücklegt.Der Radius ist der Abstand eines Objekts vom Mittelpunkt des Kreises.Winkelverschiebung ist ein Wert, den wir wissen wollen.

2. Setze die Werte der linearen Verschiebung und des Radius in die Gleichung ein. Denken Sie daran, dass der Radius der Abstand vom Mittelpunkt eines Kreises zum Rand ist; es kann sein, dass der Durchmesser für ein Problem angegeben ist, in diesem Fall müssen Sie ihn durch 2 teilen, um den Radius (Radius) des Kreises zu finden.

3. Teilen Sie die lineare Verschiebung durch den Radius.Dadurch erhalten Sie die Winkelverschiebung des Objekts.
Teil 5 von 5: Verdrängung verstehen

1. Es ist wichtig, das zu verstehen "Distanz" bedeutet manchmal etwas anderes als "Verschiebung."Die Entfernung sagt etwas darüber aus, wie weit sich ein Objekt insgesamt bewegt hat.
- Distanz nennen wir auch a "Skalar" zu erwähnen. Es zeigt an, wie viel Entfernung Sie zurückgelegt haben, sagt jedoch nichts über die Richtung aus, in die Sie sich bewegt haben.
- Gehst du zum Beispiel 2 Meter nach Osten, 2 Meter nach Süden, 2 Meter nach Westen und wieder 2 Meter nach Norden, bist du wieder am Ausgangspunkt. Obwohl Sie eine Gesamtstrecke von 10 Metern zurückgelegt haben, beträgt Ihre Verschiebung 0 Meter, da Ihr Endpunkt gleich Ihrem Startpunkt ist.

2. Die Verschiebung ist die Differenz zwischen zwei Punkten. Die Verschiebung ist keine Summe von Bewegungen, wie dies bei der Entfernung der Fall ist; Es geht nur um den Teil zwischen deinem Start- und deinem Endpunkt.

3. Merk dir die Worte gut "Hin und her" wenn du versuchst dir eine Verschiebung vorzustellen. Die entgegengesetzte Richtung macht die Bewegung in die ursprüngliche Richtung rückgängig.

4. Die Verschiebung wird entlang einer Geraden gemessen, nicht entlang einer Kreisbahn. Um die Bewegung herauszufinden, sucht man den kürzesten Weg zwischen zwei verschiedenen Punkten.

5. Bitte haben Sie Verständnis dafür, dass die Verschiebung im Gegensatz zur Distanz auch einen negativen Wert haben kann. Wenn der Endpunkt erreicht wird, indem Sie sich in eine Richtung entgegengesetzt der von Ihnen gestarteten Richtung (relativ zum Startpunkt) bewegen, ist Ihre Verschiebung negativ.

6. Erkenne, dass die Entfernungs- und Verschiebungswerte manchmal gleich sein können. Wenn Sie 25 Meter geradeaus gehen und dann anhalten, ist die zurückgelegte Strecke gleich der Verschiebung, einfach weil Sie die Richtung nicht geändert haben.
Tipps
- Genau arbeiten
- Merken Sie sich die Formeln nicht aus, sondern versuchen Sie zu verstehen, wie sie funktionieren
Notwendigkeiten
- Taschenrechner
- Entfernungsmesser
Оцените, пожалуйста статью