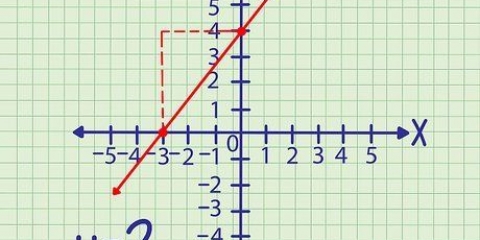
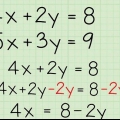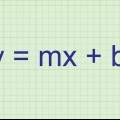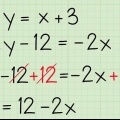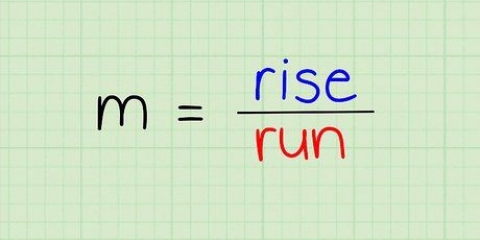Punkte sind leicht zu bestimmen, wenn Sie eine Linie auf Millimeterpapier gezeichnet haben. Um einen Punkt zu bestimmen, ziehen Sie eine gestrichelte Linie von der horizontalen Achse nach oben, bis sie die Linie schneidet. Die Position, an der Sie die Linie auf der horizontalen Achse begonnen haben, ist die x-Koordinate, während die y-Koordinate der Punkt ist, an dem die gestrichelte Linie die Linie auf der vertikalen Achse schneidet. Zum Beispiel: Linie l hat die Punkte (1, 5) und (-2, 4) während line R hat die Punkte (3, 3) und (1, -4). 
Zur Steigung der Linie l zu berechnen: Steigung = (5 - (-4))/(1 - (-2)) Subtrahieren: Steigung = 9/3 Teilen: Steigung = 3 Die Steigung der Linie R = (3 - (-4))/(3 - 1) = 7/2 
In diesem Beispiel ist 3 ungleich 7/2, also sind diese beiden Geraden nicht parallel. 

Zum Beispiel: Schreiben Sie die Linie 4y-12x=20 als Steigungsformel um. Addiere 12x zu beiden Seiten der Gleichung: 4y - 12x + 12x = 20 + 12x Teilen Sie jede Seite durch 4, um y zu isolieren: 4y/4 = 12x/4 +20/4 Steigungsformel: y = 3x + 5 
In unserem Beispiel hat die erste Linie eine Gleichung von y = 3x + 5, also ist die Steigung 3. Die andere Gerade hat eine Gleichung von y = 3x - 1, die ebenfalls eine Steigung von 3 . hat. Da die Steigungen identisch sind, sind diese beiden Linien parallel. Beachten Sie, dass, wenn diese Gleichungen den gleichen Schnittpunkt mit der y-Achse haben, sie die gleiche Linie anstatt parallel wären. 

Die Linie, die wir parallel machen wollen, ist y = -4x + 3. In dieser Gleichung repräsentiert -4 die Variable m und damit die Steigung der Geraden. 
In unserem Beispiel verwenden wir die Koordinate (1, -2). 
In unserem Beispiel mit Steigung (m) -4 und (x, y) Koordinate (1, -2) wird daraus: y – (-2) = -4(x – 1) 
Zum Beispiel: y - (-2) = -4(x - 1) Zwei Negative ergeben ein Positives: y + 2 = -4(x -1) Verwenden Sie die Verteilungseigenschaft -4(x -1) berechnen: y + 2 = -4x + 4. Subtrahiere -2 von beiden Seiten: y + 2 - 2 = -4x + 4 - 2 Die vereinfachte Gleichung: y = -4x + 2
Bestimme, ob zwei geraden parallel sind
Parallele Linien sind zwei Linien in einer Ebene, die sich niemals schneiden werden (d.h. sie werden ewig andauern, ohne sich jemals zu berühren). Ein wichtiges Merkmal paralleler Linien ist, dass sie identische Steigungen haben. Die Steigung einer Linie ist definiert als Steigung (Änderung der y-Koordinaten) über das Gefälle (Änderung der x-Koordinaten) einer Linie, also wie steil die Linie ist. Parallele Linien werden oft durch zwei vertikale Linien dargestellt (ll). Zum Beispiel zeigt AB11CD an, dass die Linie AB parallel zu CD . ist.
Schritte
Methode 1 von 3: Vergleich der Steigung jeder Linie

1. Finden Sie die Formel für die Steigung. Die Steigung (Steigung) einer Linie ist definiert durch (Y2 - Ja1)/(X2 - x1) wobei X und Y die horizontalen und vertikalen Koordinaten von Punkten auf der Linie sind. Sie müssen zwei Punkte auf der Linie bestimmen, um diese Formel zu berechnen. Der Punkt näher am Ende der Linie ist (X1, Ja1) und der Punkt weiter oben auf der Linie, über dem ersten Punkt, ist (X2, Ja2).
- Diese Formel kann umformuliert werden als Zunahme über die Distanz. Es ist die vertikale Änderung im Vergleich zur horizontalen Änderung oder die Steilheit der Linie.
- Wenn eine Linie nach rechts und oben zeigt, hat sie eine positive Steigung.
- Wenn die Linie nach rechts und unten zeigt, hat sie eine negative Steigung.

2. Identifizieren Sie die X- und Y-Koordinaten von zwei Punkten auf jeder Linie. Ein Punkt auf einer Linie wird durch seine Koordinate (X, Y) angegeben, wobei X die Position auf der horizontalen Achse und Y die Position auf der vertikalen Achse ist. Um die Steigung zu berechnen, müssen Sie auf jeder der fraglichen Linien zwei Punkte bestimmen.

3. Verarbeiten Sie die Punkte für jede Linie in der Steigungsformel. Um die Steigung zu berechnen, geben Sie die Zahlen ein, subtrahieren und dividieren. Stellen Sie sicher, dass Sie die Koordinaten im richtigen x- und y-Wert in die Formel einfügen.

4. Vergleichen Sie die Steigungen jeder Linie. Denken Sie daran, dass zwei Geraden nur dann parallel sind, wenn sie die gleiche Steigung haben. Linien können auf dem Papier parallel erscheinen und sogar sehr parallel sein, aber wenn ihre Steigungen nicht genau gleich sind, sind sie nicht parallel.
Methode 2 von 3: Verwenden der Neigungs- und Schnittpunktformel

1. Finden Sie die Formel für Steigung und Schnittpunkt einer Geraden. Die Steigungsformel, die Gleichung einer Geraden. ist y = mx + b, wobei m die Steigung ist, b der Schnittpunkt mit der y-Achse ist und x und y Variablen sind, die Koordinaten auf der Linie darstellen -- im Allgemeinen sehen Sie sie als x und y in der Gleichung. In dieser Form können Sie die Steigung der Geraden leicht als Variable `m` bestimmen.
- Ein Beispiel: 4y umschreiben - 12x = 20 und y = 3x -1. Die Gleichung 4y - 12x = 20 muss mit Algebra umgeschrieben werden, während y = 3x -1 bereits die Form der Steigungsformel hat und nicht umgeschrieben werden muss.

2. Schreiben Sie die Formel der Geraden als Steigungsformel um. Oft hat die Formel der Linie, die Sie erhalten, nicht die Form einer schiefen Ebene. Es braucht nur ein wenig Mathematik und eine variable Neuanordnung, um es in die Form der Steigungsformel zu bekommen.

3. Vergleichen Sie die Steigungen jeder Linie. Denken Sie daran, dass zwei Linien, die parallel zueinander sind, genau die gleiche Steigung haben. Mit der Gleichung y = mx + b, wobei m die Steigung der Geraden ist, können Sie die Steigung zweier Geraden ermitteln und vergleichen.
Methode 3 von 3: Bestimmen einer parallelen Linie mit der Punkt-Neigungs-Gleichung

1. Definieren Sie die Punkt-Steigungs-Gleichung. Mit der Punkt-Neigungs-Gleichung können Sie die Gleichung einer Geraden schreiben, wenn Sie die Steigung kennen und eine (x, y)-Koordinate haben. Sie verwenden diese Formel, wenn Sie eine zweite parallele Linie auf einer bereits gegebenen Linie mit einer bestimmten Steigung definieren möchten. Die Formel ist y – y1= m(x – x1) wobei m die Steigung der Geraden ist, x1 die x-Koordinate eines gegebenen Punktes auf der Geraden und y1 die y-Koordinate dieses Punktes. Wie in der Steigungsformel sind x und y Variablen, die Koordinaten auf der Linie darstellen – im Allgemeinen bleiben sie als x und y in der Gleichung.
- Die folgenden Schritte erarbeiten dieses Beispiel: Schreiben Sie die Gleichung einer Linie parallel zur Linie y = -4x + 3 durch den Punkt (1, -2).

2. Finden Sie die Steigung der ersten Linie. Wenn Sie die Gleichung einer neuen Geraden schreiben, müssen Sie zuerst die Steigung der Geraden bestimmen, zu der Ihre Gerade parallel sein muss. Stellen Sie sicher, dass die Gleichung der ursprünglichen Linie eine Steigungsformel ist, damit Sie die Steigung (m) sofort kennen.

3. Identifizieren Sie einen Punkt auf der neuen Linie. Diese Gleichung funktioniert nur, wenn Sie eine Koordinate haben, die durch die neue Linie geht. Stellen Sie sicher, dass Sie keine Koordinate wählen, die sich auf der ursprünglichen Linie befindet. Wenn Ihre endgültigen Gleichungen denselben y-Achsenabschnitt haben, sind sie nicht parallel, sondern dieselbe Linie.

4. Schreiben Sie die Gleichung der neuen Geraden in der Punkt-Steigungs-Form. Denken Sie daran, die Formel lautet: y – y1= m(x – x1). Geben Sie die Steigung und die Koordinaten Ihres Punktes ein, um die Gleichung Ihrer neuen Linie parallel zur ersten zu machen.

5. Vereinfachen Sie die Gleichung. Nachdem Sie die Zahlen eingegeben haben, kann die Gleichung zu der gebräuchlicheren Steigungsformel vereinfacht werden. Die Linie dieser Gleichung, wenn sie in einem Koordinatensystem gezeichnet wird, ist parallel zu der gegebenen Gleichung.
"Bestimme, ob zwei geraden parallel sind"
Оцените, пожалуйста статью