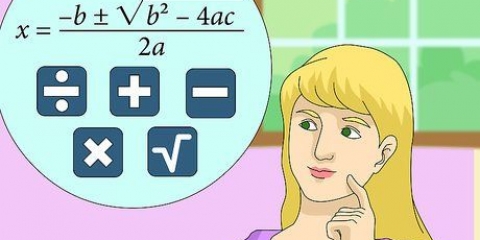Algebra lernen (mit Bildern)

Schritte
Tipps

Algebra zu lernen ist wichtig, um in fast jedem Teil der Mathematik in der Sekundar- und Hochschulbildung voranzukommen. Jede Mathestufe baut auf dem Fundament auf und damit ist jede Mathestufe besonders wichtig. Allerdings können selbst die grundlegendsten mathematischen Fähigkeiten für Anfänger schwer zu erlernen sein, wenn sie zum ersten Mal konfrontiert werden. Wenn Sie mit grundlegenden Themen der Algebra zu kämpfen haben, machen Sie sich keine Sorgen. Mit einer kleinen Erklärung, ein paar einfachen Beispielen und einigen Tipps zur Verbesserung Ihrer Fähigkeiten werden Sie bald ein Meister der Algebra.

Schritte

Teil 1 von 5: Die Grundregeln der Algebra lernen

1. Überprüfen Sie grundlegende mathematische Fähigkeiten. Um Algebra zu lernen, müssen Sie die Grundfertigkeiten wie Addition, Subtraktion, Multiplikation und Division beherrschen. Diese mathematischen Fähigkeiten, die Sie in der Grundschule lernen, sind unerlässlich, bevor Sie mit Algebra beginnen. Wenn Sie diese Fähigkeiten nicht beherrschen, wird es schwierig, die komplexeren Konzepte der Algebra zu erlernen. Wenn du eine Auffrischung dieser Operationen brauchst, schau in wikiHow nach, um Artikel über die Grundlagen der Mathematik zu finden.

Es ist nicht notwendig, sehr gut im Kopfrechnen zu sein, wenn Sie Algebra gut können. Während des Mathematikunterrichts darfst du oft mit einem Taschenrechner arbeiten, um beim Rechnen Zeit zu sparen. Sie sollten auf jeden Fall ohne Taschenrechner rechnen können, falls Sie ihn nicht benutzen dürfen.

2. Erfahren Sie die Reihenfolge der Operationen. Eines der schwierigsten Dinge beim Lösen einer mathematischen Gleichung ist zu wissen, wo man anfangen soll. Glücklicherweise gibt es eine bestimmte Reihenfolge, in der Sie diese Probleme lösen: Zuerst kommen die Terme in Klammern, dann die Exponenten/Potenzen, dann die Multiplikation, Division, Addition und schließlich Subtraktion. Ein praktischer Merksatz, um sich an die Abfolge der Operationen zu erinnern, ist "How Should We Get Rid Of The Insufficients" (oder als Akronym HMWVDOA). Siehe wikiHow für Artikel zum Anwenden der Operationsreihenfolge. Zur Erinnerung hier noch einmal die Abfolge der Operationen:

huhFledermäuse

macht erhöhen

Wzucken

Vmultiplizieren

Özählen

einsubtrahieren

Die Reihenfolge der Operationen ist in der Mathematik wichtig, da eine falsche Reihenfolge dazu führen kann, dass eine andere Antwort gefunden wird. Wenn Sie beispielsweise das Problem 8 + 2 × 5 haben und zuerst 2 zu 8 addieren, erhalten Sie 10 × 5 =50 als antwort. Aber wenn Sie zuerst 2 mit 5 multiplizieren, folgt 8 + 10 =18. Nur die zweite Antwort ist richtig.

3. Erfahren Sie, wie Sie negative Zahlen verwenden. Es ist in der Algebra üblich, negative Zahlen zu verwenden, daher ist es eine gute Idee, sich vor dem Übergang zur Algebra zu besprechen, wie negative Zahlen addiert, subtrahiert, multipliziert und dividiert werden. Im Folgenden finden Sie nur einige Grundlagen der Arbeit mit negativen Zahlen, die Sie sich merken müssen – für weitere Informationen lesen Sie die wikiHow-Artikel über Addition, Subtraktion und Division und Multiplikation negativer Zahlen.

Auf einem Zahlenstrahl ist eine negative Version einer Zahl genauso weit von Null entfernt wie auf der positiven Seite, jedoch in die entgegengesetzte Richtung.

Die Addition zweier negativer Zahlen ergibt die Summe negativer (mit anderen Worten, die Zahlen werden größer, aber da die Zahl negativ ist, ist es eine niedrigere Zahl).

Zwei negative Vorzeichen heben sich gegenseitig auf – das Subtrahieren einer negativen Zahl ist das gleiche wie das Addieren einer positiven Zahl.

Das Multiplizieren oder Dividieren von zwei negativen Zahlen ergibt eine positive Antwort.

Das Multiplizieren oder Dividieren einer positiven Zahl und einer negativen Zahl ergibt eine negative Antwort.

4. Erfahren Sie, wie Sie lange Probleme organisieren. Während einfache Algebraprobleme oft leicht zu lösen sind, können kompliziertere Probleme viele Schritte erfordern. Um Fehler zu vermeiden, beginnen Sie jedes Mal in einer neuen Zeile, wenn Sie bei der Lösung des Problems einen Schritt weiter sind. Wenn Sie es mit einer Gleichung mit Termen auf zwei Seiten des Gleichheitszeichens zu tun haben, versuchen Sie, diese Zeichen (`=`) untereinander zu schreiben. Auf diese Weise ist jeder Fehler in Ihrer Berechnung viel einfacher zu erkennen.

Um zum Beispiel die Gleichung 9/3 - 5 + 3 × 4 zu lösen, würden wir unser Problem so anordnen:

9/3 - 5 + 3×4

9/3 - 5 + 12

3 - 5 + 12

3 + 7

Teil 2 von 5: Variablen verstehen

1. Suchen Sie nach Symbolen, die keine Zahlen sind. In der Algebra haben Sie es in Ihren mathematischen Aufgaben mit Buchstaben und Symbolen zu tun und nicht nur mit Zahlen. Diese werden Variablen genannt. Variablen sind nicht so schwierig, wie sie auf den ersten Blick erscheinen – sie sind nur Möglichkeiten, Zahlen mit unbekannten Werten darzustellen. Nachfolgend finden Sie einige gängige Beispiele für Variablen in der Algebra:

Buchstaben wie x, y, z, a, b und c
Griechische Buchstaben wie Theta oder θ
Beachten Sie, dass nicht alle Symbole sind unbekannte Variablen. Zum Beispiel: pi oder π, immer gleich (aufgerundet) 3,1459.

2. Stellen Sie sich Variablen als `unbekannte` Zahlen vor. Wie oben erwähnt, sind Variablen im Allgemeinen nur Zahlen mit unbekannten Werten. Mit anderen Worten, es gibt eine Zahl die an die Stelle der Variablen treten kann, damit die Gleichung funktioniert. Normalerweise besteht das Ziel eines Algebra-Problems darin, herauszufinden, was diese Variable ist – betrachten Sie sie als eine "mysteriöse Zahl", die Sie zu entdecken versuchen.

In der Gleichung 2x + 3=11 ist x beispielsweise die Variable. Dies bedeutet, dass es einen Wert gibt, der für x ersetzt werden kann, um die linke Seite der Gleichung gleich 11 . zu machen. Da 2 × 4 + 3=11, in diesem Fall x=4.

Eine einfache Möglichkeit, Variablen zu verstehen, besteht darin, sie in Algebraaufgaben durch ein Fragezeichen zu ersetzen. Zum Beispiel: Schreiben Sie die Gleichung 2 + 3 + x = 9 um als 2 + 3 + ?=9. Dies macht es leicht zu erkennen, worum es geht – wir müssen herausfinden, welche Zahl wir zu 2 + 3 = 5 addieren müssen, um 9 als Antwort zu erhalten. Die Antwort ist wieder 4, natürlich.

3. Wenn eine Variable mehrmals vorkommt, vereinfachen Sie die Variablen. Was tun, wenn dieselbe Variable mehrmals in einer Gleichung vorkommt?? Obwohl dies eine schwierige Situation sein mag, können Sie Variablen genauso behandeln wie normale Zahlen – mit anderen Worten, Sie können addieren, subtrahieren usw. solange Sie nur Variablen kombinieren, die gleich sind. Mit anderen Worten, x + x=2x, aber x + y ist nicht gleich 2xy.

Zum Beispiel: Betrachten Sie die Gleichung 2x + 1x=9. In diesem Fall addieren wir 2x und 1x zusammen, um 3x=9 . zu erhalten. Wegen 3 x 3=9 wissen wir nun, dass x=3.

Beachten Sie erneut, dass Sie nur Variablen hinzufügen können, die gleich sind. In der Gleichung 2x + 1y=9 können wir 2x und 1y nicht kombinieren, da es sich um zwei verschiedene Variablen handelt.

Dies gilt auch, wenn eine Variable einen anderen Exponenten hat als die andere. In der Gleichung 2x + 3x=10 können 2x und 3x beispielsweise nicht kombiniert werden, da die x-Variablen unterschiedliche Exponenten haben. Weitere Informationen zum Hinzufügen von Exponenten findest du in wikiHow.

Teil 3 von 5: Gleichungen durch Eliminieren lösen

1. Isolieren Sie die Variable in der Gleichung. Das Lösen einer Gleichung in der Algebra beinhaltet im Allgemeinen den Versuch, die Variable zu bestimmen. Algebraische Gleichungen haben normalerweise auf beiden Seiten Zahlen und/oder Variablen, wie folgt: x + 2=9 × 4. Um zu bestimmen, was die Variable ist, müssen Sie sie auf einer Seite des Gleichheitszeichens platzieren. Was auf der anderen Seite des Gleichheitszeichens übrig bleibt, ist die Antwort.

Im Beispiel (x + 2=9 × 4), um x von der linken Seite der Gleichung zu isolieren, müssen wir `+2` loswerden. Dazu subtrahieren wir 2 von dieser Seite und lassen x=9 × 4. Um beide Seiten der Gleichung gleich zu machen, müssen wir auch 2 von der anderen Seite subtrahieren. Dies lässt uns mit x=9 × 4 – 2. Gemäß der Reihenfolge der Operationen multiplizieren wir zuerst, subtrahieren dann und erhalten x=36 - 2=34.

2. Eliminiere Addition durch Subtraktion (und umgekehrt). Wie wir oben gesehen haben, bedeutet das Isolieren von x auf einer Seite des Gleichheitszeichens normalerweise den Versuch, die unmittelbar angrenzenden Zahlen loszuwerden. Sie tun dies, indem Sie auf beiden Seiten der Gleichung die `Gegensatz`-Operation ausführen. In der Gleichung x + 3=0 setzen wir zum Beispiel auf beiden Seiten eine `- 3`, weil neben x . eine `+ 3` steht. Dadurch wird x isoliert und `-3` auf der anderen Seite des Gleichheitszeichens erhalten, wie folgt: x=-3.

Im Allgemeinen sind Addition und Subtraktion „entgegengesetzt“ – man arbeitet so. Siehe unten:

Beim Addieren, Subtrahieren. Beispiel: x + 9=3 → x=3 - 9

Beim Subtrahieren, Addieren. Beispiel: x - 4=20 → x=20 + 4

3. Eliminiere die Multiplikation durch Dividieren (und umgekehrt). Multiplikation und Division sind etwas schwieriger zu handhaben als Addition und Subtraktion, aber sie haben die gleiche "entgegengesetzte" Beziehung. Wenn Sie auf einer Seite ein `×3` sehen, können Sie es eliminieren, indem Sie beide Seiten durch 3 teilen.

Bei Multiplikation und Division müssen Sie die umgekehrte Operation auf ausführen alles auf der anderen Seite des Gleichheitszeichens, auch wenn es mehr als eine Zahl ist. Siehe unten:

Beim Multiplizieren, Dividieren. Beispiel: 6x=14 + 2→ x=(14 + 2)/6

Beim Dividieren, Multiplizieren. Beispiel: x/5=25 → x=25 × 5

4. Eliminiere Exponenten durch Ziehen von Quadratwurzeln (und umgekehrt). Exponenten sind ein fortgeschrittenes Thema in der Algebra – wenn du nicht weißt, was du mit ihnen anfangen sollst, lies den wikiHow-Einsteigerartikel über Exponenten. Das `Gegenteil` eines Exponenten ist die Wurzel hoch dieser Zahl. Zum Beispiel ist das Gegenteil des Exponenten die Quadratwurzel (√), das Gegenteil des Exponenten ist die Kubikwurzel (√), etc.

Dies kann etwas verwirrend sein, aber in diesen Fällen ziehen Sie die Quadratwurzel beider Seiten, wenn Sie es mit einem Exponenten zu tun haben. Andererseits nimmt man auch den Exponenten beider Seiten, wenn man es mit einer Quadratwurzel zu tun hat. Siehe unten:

Für Exponenten ziehe die Quadratwurzel. Beispiel: x=49 → x=49

Für Wurzeln nimm den Exponenten. Beispiel: √x=12 → x=12

Teil 4 von 5: Verbessere deine mathematischen Fähigkeiten

1. Verwenden Sie Bilder, um Probleme deutlicher zu machen. Wenn Sie ein Algebraproblem nicht darstellen können, verwenden Sie Grafiken oder Bilder, um die Gleichung zu veranschaulichen. Sie können sogar eine Gruppe von Objekten (wie Blöcke oder Münzen) verwenden, wenn Sie diese zur Hand haben.

Lassen Sie uns zum Beispiel die Gleichung x + 2=3 mithilfe von Boxen (☐) lösen
x +2=3
☒+☐☐=☐☐☐
Ziehen Sie an dieser Stelle 2 von beiden Seiten ab, indem Sie 2 Quadrate (☐☐) von beiden Seiten entfernen:
☒+☐☐-☐☐=☐☐☐-☐☐
☒=☐, oder x=1
Ein weiteres Beispiel: 2x=4
=☐☐☐☐
An dieser Stelle teilen wir beide Seiten durch zwei und teilen die Kästen auf beiden Seiten in zwei Gruppen:
|☒=☐☐|☐☐
☒=☐☐, oder x=2

2. Verwenden Sie `logische Prüfungen` (insbesondere bei Problemen). Wenn Sie ein Problem in eine algebraische Gleichung umwandeln müssen, überprüfen Sie Ihre Formel, indem Sie einfache Werte in den Variablen verarbeiten. Ist Ihre Gleichung richtig, wenn x=0? Wenn x=1? Wenn x=-1? Es ist leicht, kleine Fehler zu machen, wenn Sie so etwas wie p=6d notieren, wenn Sie p=d/6 meinen, aber Sie werden diese schnell genug erkennen, wenn Sie Ihre Arbeit überprüfen, bevor Sie fortfahren.

Beispiel: Angenommen, wir haben ein Fußballfeld, das 30 Meter länger als breit ist. Wir verwenden die Gleichung l=w + 30, um dies darzustellen. Wir können diese Gleichung testen, indem wir einfache Werte für w . eingeben. Wenn das Feld beispielsweise w = 10 Meter breit ist, ist es 10 + 30 = 40 Meter lang. Wenn es 30 Meter breit ist, dann ist es 30 + 30 = 60 Meter lang usw. Dies erscheint logisch – wir erwarten, dass das Feld mit zunehmender Breite länger wird, daher scheint diese Gleichung eine vernünftige Lösung zu sein.

3. Denken Sie daran, dass die Antworten in der Mathematik nicht immer ganze Zahlen sind. Antworten in der Algebra und anderen Zweigen der Mathematik sind nicht immer runde, einfache Zahlen. Oft sind es Dezimalzahlen, Brüche oder irrationale Zahlen. Ein Taschenrechner kann Ihnen helfen, diese komplizierten Antworten zu finden, aber denken Sie daran, dass Ihr Lehrer Sie möglicherweise auffordert, die Antwort genau und nicht in einer plumpen Dezimalzahl anzugeben.

Angenommen, wir reduzieren eine algebraische Gleichung auf x=1250. Wenn wir 1250 in einen Taschenrechner eingeben, erhalten wir eine riesige Reihe von Dezimalstellen (da der Bildschirm des Taschenrechners nur wenig Platz hat, kann er nicht die vollständige Antwort anzeigen). In diesem Fall können wir die Antwort einfach als 1250 anzeigen oder die Antwort vereinfachen, indem wir sie in wissenschaftlicher Schreibweise schreiben.

4. Wenn Sie mit den Grundlagen der Algebra vertraut sind, versuchen Sie es mit Factoring. Eine der kniffligeren Fähigkeiten in der Algebra ist das Faktorisieren – eine Art Abkürzung, um komplexe Gleichungen in einfacherer Form zu schreiben. Factoring ist ein ziemlich fortgeschrittenes Thema in der Algebra, also lesen Sie den oben verlinkten Artikel, wenn Sie Schwierigkeiten damit haben. Hier sind einige Tipps zum Faktorisieren von Gleichungen:

Faktorisiere Gleichungen der Form ax + ba zu a(x + b). Beispiel: 2x + 4=2(x + 2)

Faktorisieren von Gleichungen der Form ax + bx zu cx((a/c)x + (b/c)) wobei c die größte Zahl ist, die a und b vollständig passen. Beispiel: 3y + 12y=3y(y + 4)

Gleichungen der Form x + bx + c faktorisieren in (x + y)(x + z) wobei y × z=c und yx + zx=bx. Beispiel: x + 4x + 3=(x + 3)(x + 1).

5. Üben, üben, üben! Fortschritte beim Erlernen von Algebra (und jedem anderen Zweig der Mathematik) erfordern viel harte Arbeit und Wiederholungen. Machen Sie sich keine Sorgen – wenn Sie im Unterricht aufmerksam sind, alle Ihre Hausaufgaben machen und bei Bedarf Ihren Lehrer oder andere Schüler um Hilfe bitten, wird Algebra irgendwann zur zweiten Natur.

6. Bitte deinen Lehrer, dir bei den schwierigeren Fächern zu helfen. Machen Sie sich keine Sorgen, wenn es Ihnen schwerfällt, das Material zu meistern – Sie müssen es nicht selbst lernen. Dein Lehrer ist die erste Person, die dir bei Fragen hilft. Bitte den Lehrer nach dem Unterricht höflich um Hilfe. Gute Lehrer sind in der Regel bereit, ein Thema bei einem Besuch nach dem Unterricht noch einmal zu erklären und können Ihnen sogar zusätzliches Übungsmaterial zur Verfügung stellen.

Wenn Ihr Lehrer Ihnen aus irgendeinem Grund nicht helfen kann, fragen Sie ihn nach Nachhilfemöglichkeiten in der Schule. Viele Schulen haben zusätzliche Klassen, die Ihnen die zusätzliche Zeit und Aufmerksamkeit geben, die Sie brauchen, um in Algebra zu übertreffen. Denken Sie daran, dass Sie sich nicht schämen müssen, wenn Sie die kostenlose Hilfe in Anspruch nehmen – es ist ein Zeichen dafür, dass Sie schlau genug sind, um Ihre Probleme zu lösen!

Teil5 von 5:Erkunden von fortgeschrittenen Themen

1. Erfahren Sie, wie Sie eine Gleichung grafisch darstellen. Diagramme sind wertvolle Werkzeuge in der Algebra, da Sie Ideen, die normalerweise Zahlen erfordern, in leicht verständlichen Bildern darstellen können. Wenn Sie mit Algebra beginnen, sind Graphen normalerweise auf Probleme von Gleichungen mit zwei Variablen (normalerweise x und y) beschränkt und werden in einem einfachen 2D-Graphen mit einer x-Achse und einer y-Achse dargestellt. Bei diesen Gleichungen müssen Sie nur einen Wert für x einsetzen und dann nach y auflösen (oder umgekehrt), um zwei Zahlen zu erhalten, die einem Punkt im Diagramm entsprechen.

In der Gleichung y=3x ersetzen wir beispielsweise x durch 2 und erhalten y=6 als Antwort. Dies bedeutet, dass der Punkt (2.6) (zwei Punkte rechts vom Nullpunkt und 6 nach oben) ist Teil des Graphen der Gleichung.
Gleichungen der Form y=mx + b (wobei m und b Zahlen sind) sind Besondere nur innerhalb der Grundlagen der Algebra. Diese Gleichungen haben immer die Steigung m und schneiden die y-Achse im Punkt y=b.

2. Erfahren Sie, wie Sie Ungleichungen lösen können. Was tun, wenn eine Gleichung kein Gleichheitszeichen hat?? Nichts Besonderes im Vergleich zu dem, was Sie anders machen würden, stellt sich heraus. In Ungleichungen, wo man auf Zeichen trifft wie, > (`größer als`) und< (`kleiner als`), lösen Sie die Gleichung wie zuvor. Die Antwort, die Sie erhalten, ist entweder kleiner oder größer als Ihre Variable.

Zum Beispiel in der Gleichung 3 > 5x - 2 lösen wir dies wie eine normale Gleichung:

3 > 5x - 2

5 > 5x

1 > x, oder x< 1.

Dies impliziert, dass jede Zahl kleiner als 1 ist richtig für x. Mit anderen Worten, x kann 0, -1, -2 usw. sein. sind. Wenn wir diese Zahlen in die Gleichung für x einsetzen, erhalten wir immer eine Antwort kleiner als 3.

3. Quadratische oder quadratische Gleichungen lösen. Ein algebraisches Thema, über das viele Anfänger stolpern, ist das Lösen quadratischer Gleichungen. Dies sind Gleichungen der Form ax + bx + c=0, wobei a, b und c Zahlen sind (außer dass a nicht 0 sein kann). Wir lösen diese Gleichungen mit der Formel x=[-b +/- √(b - 4ac)]/2a . Seien Sie vorsichtig – das +/- bedeutet, dass Sie die Antworten für beide Additionen finden müssen wenn subtrahieren, sodass es zwei mögliche Antworten für diese Art von Problem gibt.

Ein Beispiel: Lösen der quadratischen Formel 3x + 2x -1=0.

x=[-b +/- √(b - 4ac)]/2a

x=[-2 +/- √(2 - 4(3)(-1))]/2(3)

x=[-2 +/- (4 - (-12))]/6

x=[-2 +/- √(16)]/6

x=[-2 +/- 4]/6

x=-1 und 1/3

4. Experimentieren Sie mit dem Gleichungssystem. Das gleichzeitige Lösen mehrerer Gleichungen kann sehr schwierig klingen, aber wenn Sie mit einfachen algebraischen Gleichungen arbeiten, ist es nicht so schwer. Mathematiklehrer verwenden oft eine Grafik, um diese Probleme zu lösen. Wenn Sie mit Systemen aus zwei Gleichungen arbeiten, finden Sie die Lösung, indem Sie sich die Punkte im Graphen ansehen, an denen sich die Geraden der beiden Gleichungen schneiden.

Beispiel: Angenommen, wir haben es mit einem Gleichungssystem y=3x - 2 und y=-x - 6 . zu tun. Wenn wir diese beiden Linien in einen Graphen zeichnen, erhalten wir eine Linie, die steil ansteigt und eine, die weniger steil abfällt. Da sich diese Linien im Punkt schneiden (-1,-5), ist, dass die Lösung des Systems.

Wenn Sie dies überprüfen möchten, verarbeiten Sie die Antwort in den Gleichungen des Systems – eine gute Antwort sollte für beide Gleichungen „funktionieren“.

y=3x - 2

-5=3(-1) - 2

-5=-3 - 2

-5=-5

y=-x - 6

-5=-(-1) - 6

-5=1 - 6

-5=-5

Beide Gleichungen sind `richtig`, also ist unsere Antwort richtig!

Tipps

Es gibt unzählige Ressourcen für Leute, die Algebra online lernen möchten. Nur eine einfache Suche in einer Suchmaschine wie `Algebra Help` kann Dutzende von großartigen Ergebnissen liefern. Schauen Sie sich auch die an Kategorie Mathematik. Dort findet ihr viele Informationen, also gleich loslegen!
Eine großartige Seite für Algebra-Anfänger ist khanacademy.com. Diese kostenlose Website bietet viele leicht verständliche Lektionen zu einer Vielzahl von Themen, einschließlich Algebra. Es gibt Videos zu allem, von extrem einfachen bis zu universitären Themen, also zögere nicht, die Khan Academy und all die Hilfe, die dir diese Seite geben kann, zu nutzen!
Denken Sie daran, dass die besten Ressourcen zum Erlernen von Algebra Menschen sind, die Sie bereits kennen. Wenden Sie sich an Freunde oder andere Schüler derselben Klasse, wenn Sie Hilfe bei den im Unterricht behandelten Themen benötigen.

"Algebra lernen"

Lernen ohne langeweile

Mathe lernen

Einen test bestehen, ohne zu lernen

Konstruktionszeichnungen lesen lernen

Оцените, пожалуйста статью