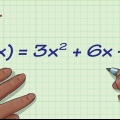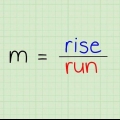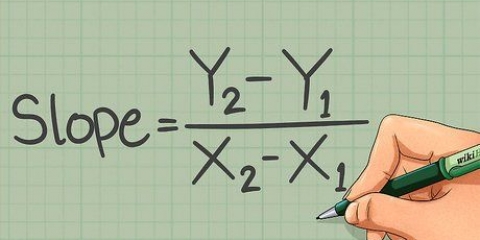Die Steigung einer Linie bestimmen

Schritte

Die Steigung einer Linie ist ein Maß dafür, wie schnell sich die Linie ändert. Dies kann mit einer geraden Linie erfolgen – wobei die Steigung genau angibt, wie weit nach oben (positive Steigung) oder nach unten (negative Steigung) eine Linie über eine bestimmte Distanz geht. Die Steigung kann auch für eine Tangente an eine Kurve verwendet werden. Oder es könnte eine gekrümmte Linie sein, die in der Analysis verwendet wird, wobei die Steigung auch als „Ableitung“ einer Funktion bekannt ist. Wie auch immer, stellen Sie sich die Steigung einfach als die "Änderungsrate" eines Diagramms vor: Wenn die Variable "x" größer wird, mit welcher Geschwindigkeit ändert sich "y"?? So kann man sich die Steigung als Ursache und Wirkung vorstellen.

Schritte

Methode 1 von 3: Ermitteln der Steigung einer linearen Gleichung

Finden Sie die Steigung einer Gleichung Schritt 1

1. Bestimmen Sie anhand der Steigung, wie steil und in welche Richtung (nach oben oder unten) eine Linie verläuft. Die Steigung einer Geraden zu bestimmen ist einfach, solange Sie eine lineare Gleichung haben oder aufstellen können. Diese Methode funktioniert nur, wenn:

Die Variablen haben keine Exponenten.
Es gibt nur zwei Variablen und keine davon sind Brüche (beispielsweise kann Folgendes nicht sein: $\frac{1}{x}$ ${frac{1}{x}}$ )
Die Gleichung kann vereinfacht werden auf die Form $ja = m x + B$ $y=mx+b$ , wodurch m und B Konstanten (Zahlen wie 3, 10, -12, $\frac{4}{3}, \frac{3}{5}$ ${frac{4}{3}},{frac{3}{5}}$ ).

2. Finden Sie die Zahl vor dem x, normalerweise als `m` geschrieben, um die Steigung zu bestimmen. Wenn die Gleichung bereits in der richtigen Form ist,

ja = m x + B

$y=mx+b$ , dann wähle einfach die Zahl in der `m`-Position (aber wenn keine Zahl vor x steht, dann ist die Steigung 1). Das ist also auch die Steigung! Wisse, dass diese Nummer, m, wird immer mit der Variablen multipliziert, in diesem Fall ein `x`. Schauen Sie sich die folgenden Beispiele an:

ja = 2 x + 6

$y=2x+6$

Steigung = 2

ja = 2 - x

$y=2-x$

Steigung = -1

ja = \frac{3}{8} x - 10

$y={frac{3}{8}}x-10$

Steigung = $\frac{3}{8}$ ${frac{3}{8}}$

Finden Sie die Steigung einer Gleichung Schritt 3

3. Erkenne die Gleichung, bei der eine Variable isoliert ist, wenn die Steigung nicht klar ist. Sie können addieren, subtrahieren, multiplizieren usw. eine Variable isolieren (normalerweise das `y`). Denken Sie daran, dass Sie alles, was Sie auf der einen Seite des Gleichheitszeichens tun (z. B. 3 hinzufügen), auch auf der anderen Seite tun müssen. Dein ultimatives Ziel ist eine Gleichung, wie zum Beispiel

ja = m x + B

$y=mx+b$ . Zum Beispiel:

Finden Sie die Steigung von $2 ja - 3 = 8 x + 7$ $2y-3=8x+7$

Wandeln Sie es in das Formular um $ja = m x + B$ $y=mx+b$ :

2 ja - 3 + 3 = 8 x + 7 + 3

$2y-3+3=8x+7+3$

2 ja = 8 x + 10

$2y=8x+10$

2 ja 2 = 8 x + 10 2

${frac{2y}{2}}={frac{8x+10}{2}}$

ja = 4 x + 5

$y=4x+5$

Bestimmen Sie die Steigung:

Steigung = M = 4

Methode 2 von 3: Bestimmung der Steigung mit zwei Punkten

Finden Sie die Steigung einer Gleichung Schritt 4

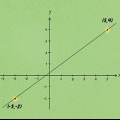
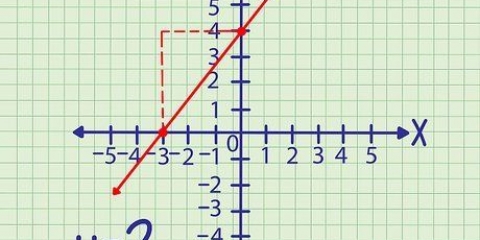
1. Verwenden Sie ein Diagramm und zwei Punkte, um schnell die Steigung ohne die Gleichung zu finden. Wenn Sie einen Graphen und eine Linie haben, aber keine Gleichung, können Sie die Steigung dennoch leicht bestimmen. Alles, was Sie brauchen, sind zwei Punkte auf der Linie, die Sie auf die Gleichung anwenden

ja 2 - {ja}_{1} x 2 - x_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Berücksichtigen Sie bei der Ermittlung der Steigung die folgenden Informationen, um sicherzugehen, dass Sie auf dem richtigen Weg sind:

Positive Steigungen gehen nach oben und nach rechts.
Negative Steigungen gehen runter und nach rechts.
Steilere Hänge sind steilere Linien. Weniger steile Hänge sind immer sanfter.
Perfekte horizontale Linien haben eine Steigung von Null.
Perfekt vertikale Linien haben überhaupt keine Neigung. Ihre Steigung (oder Steigung) ist `undefiniert`.

Finden Sie die Steigung einer Gleichung Schritt 5

2. Wählen Sie zwei Punkte aus und bringen Sie sie in die einfache (x, y)-Form. Verwenden Sie den Graphen (oder die Zuordnungsfrage), um die x- und y-Koordinaten von zwei Punkten auf dem Graphen zu finden. Sie können aus zwei beliebigen Punkten bestehen, durch die die Linie verläuft. Angenommen, bei dieser Methode geht die Linie durch den Punkt (2.4) und durch (6.6).

In jedem Paar ist die x-Koordinate die erste Zahl und die y-Koordinate ist die zweite Zahl nach dem Komma.

Jede x-Koordinate auf einer Linie hat eine entsprechende y-Koordinate.

Finden Sie die Steigung einer Gleichung Schritt 6

3. Beschrifte die Punkte x₁, ja₁, x₂, ja₂, und behalte jeden Punkt mit seinem Paar. Fahren Sie mit unserem ersten Beispiel fort und verwenden Sie die Punkte (2.4) und (6.6) und beschriften Sie die x- und y-Koordinaten jedes Punktes. Wenn alles gut gegangen ist, haben Sie jetzt am Ende:

x₁: 2

ja₁: 4

x₂: 6

ja₂: 6

Finden Sie die Steigung einer Gleichung Schritt 7

4. Ersetzen Sie diese Punkte in der `Punkt-Steigungs-Formel`, um die Steigung zu finden. Mit der folgenden Formel wird die Steigung anhand von zwei beliebigen Punkten auf einer Geraden bestimmt: $ja 2 - {ja}_{1} x 2 - x_{1}$ ${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Ersetzen Sie einfach die vier Punkte und vereinfachen Sie:

Ursprüngliche Punkte: (2.4) und (6.6).

Auf die Punkt-Steigungs-Formel anwenden:

6 - 4 6 - 2

${frac{6-4}{6-2}}$

Vereinfachen Sie für die endgültige Antwort:

$\frac{2}{4} = \frac{1}{2}$ ${frac{2}{4}}={frac{1}{2}}$ = Steigung

Finden Sie die Steigung einer Gleichung Schritt 8

5. Verstehen Sie, wie die Punkt-Steigungs-Formel funktioniert. Die Steigung einer Linie wird durch die Änderung von y von x (y/x) angezeigt: wie weit die Linie nach oben geht geteilt durch wie weit die Linie nach rechts verläuft. Die Zunahme der Linie ist die Differenz zwischen den y-Werten (denken Sie daran, die y-Achse geht nach oben und unten), und die Zunahme der Linie ist die Differenz zwischen den x-Werten (und die x-Achse geht von von links nach rechts).

Finden Sie die Steigung einer Gleichung Schritt 9

6. Erfahren Sie andere Methoden, die Sie kennen müssen, um die Steigung zu bestimmen. Die Steigungsgleichung lautet

ja 2 - {ja}_{1} x 2 - x_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Dies kann auch durch den griechischen Buchstaben `Δ` (`Delta`) dargestellt werden, was `Unterschied` bedeutet. Die Steigung kann auch als Δy/Δx dargestellt werden, was "Differenz von y" / "Differenz von x" bedeutet. Das ist genau die gleiche Frage wie "Bestimmen Sie die Steigung zwischen…"

Methode 3 von 3: Verwenden Sie die Differentialrechnung, um die Steigung einer Kurve zu finden

Finden Sie die Steigung einer Gleichung Schritt 10

1. Sehen Sie sich an, wie Sie die Ableitung gemeinsamer Funktionen auf verschiedene Weise bestimmen können. Derivate geben Ihnen die Änderungsrate (oder Steigung) an einem Punkt auf einer Linie. Die Linie kann gebogen oder gerade sein – egal. Denken Sie daran, wie sich die Linie zu einem bestimmten Zeitpunkt ändert, anstatt wie sich die Steigung der gesamten Linie ändert. Wie Sie die Ableitung bestimmen, hängt vom Funktionstyp ab. Sehen Sie sich also an, wie Sie die Ableitung von Funktionen bestimmen, bevor Sie fortfahren.

Lesen Sie hier über die Bestimmung der Ableitung
Die einfachsten Ableitungen, die für Standard-Exponentialgleichungen, Sie können mit einer schnellen Methode leicht finden. Sie werden dies im Rest der Methode verwenden.

Finden Sie die Steigung einer Gleichung Schritt 11

2. Verstehen Sie, bei welchen Problemen Sie die Steigung mithilfe von Ableitungen berechnen müssen. Sie werden nicht immer explizit nach der Ableitung oder Steigung einer Kurve gefragt. Möglicherweise werden Sie auch nach der "Änderungsrate" an Punkt (x, y) gefragt. Möglicherweise werden Sie nach einer Gleichung für die Steigung des Graphen gefragt, was einfach bedeutet, die Ableitung zu finden. Schließlich werden Sie möglicherweise nach der Steigung der Tangente in (x, y) gefragt. Dies bedeutet wiederum, dass nur die Steigung der Kurve an einem bestimmten Punkt (x, y) abgefragt wird.

Stellen Sie sich bei dieser Methode die folgende Frage: "Was ist die Steigung der Linie

F (x) = 2 x 2 + 6 x

$f(x)=2x^{2}+6x$ in Punkt (4.2)?"

Die Ableitung wird oft geschrieben als

F^{Sex} (x), {ja}^{Sex},

oder

Finden Sie die Steigung einer Gleichung Schritt 12

3.Finden Sie die Ableitung der Funktion. Sie brauchen nicht einmal einen echten Graphen, sondern nur die Funktion oder Gleichung des Graphen. In diesem Beispiel verwenden wir eine zuvor besprochene Funktion,

4x+6 $F$

Finden Sie die Steigung einer Gleichung Schritt 13

4.Ersetzen Sie den Punkt in der Ableitungsgleichung, um die Steigung zu finden. Das Differential einer Funktion gibt die Steigung der Funktion an einem bestimmten Punkt an. Mit anderen Worten, f"(x) ist die Steigung der Funktion zu einem beliebigen Zeitpunkt (x,f(x)). Also für diese Übungsaufgabe: